最小生成树

用$G=(V,E)$表示连通无向图，并且对于每条边$(u,v)\in E$，为其赋予权重$w(u,v)$。我们希望找到一个无环子集$T\subseteq E$，既能够将所有的节点连接起来，又具有最小的权重。由于T是无环的，并且连通所有结点，因此T是一棵树，称T为（图G的）生成树。称求取该生成树的问题为最小生成树问题。

讨论的两种解决最小生成树问题的两种算法：Kruskal算法和Prim算法都是贪心算法。贪心算法的每一步必须在多个可能的选择中选择一种。贪心算法推荐选择在当前看来最好的选择。这种策略一般并不能保证找到一个全局最优的解决方案。但是，对于最小生成树问题来说，可以证明某些贪心策略确实能够找到一棵权重最小的生成树。

最小生成树的形成

假设有一个连通无向图$G=(V,E)$和权重函数$w:E\to R$，两种算法都采用贪心策略，但方式不同。贪心策略可以用下面的通用方式来表示。

该通用方式在每个时刻生长最小生成树的一条边，并在整个策略的实施过程中，管理一个遵守下述循环不变式的边集合A：
$$在每遍循环之前，A是某棵最小生成树的一个子集$$
在每一步，选择一条边$(u,v)$，将其加入到集合A中，使得A不违反循环不变式，即A⋃{(u,v}A\bigcup\{(u,v\}A⋃{(u,v}也是某棵最小生成树的子集。由于可以安全地将这种边加入到集合A而不会破坏A的循环不变式，因此称这样的边为集合A的安全边。

GENERIC-MST(G,w)
    A = Ø
    while A does not form a spanning tree
        find an edge(u,v) that is safe for A
        A = A∪{(u,v)}
    return A

使用循环不变式的方式：

• 初始化

  在算法第2行之后，集合A直接满足循环不变式。

• 保持

  算法第3~5行循环通过只加入安全边来维持循环不变式。

• 终止

  所有加入到集合A的边都属于某棵最小生成树，因此，算法第5行所返回的集合A必然是一颗最小生成树。

该算法最关键的是第3行：找到一条安全边。这条安全边必然存在，因为在执行算法第3行时，循环不变式告诉我们存在一棵生成树T，满足$A\subseteq T$。在第2~4行的while循环体内，集合A一定是T的真子集，因此，必然存在一条边$(u,v)\in T$，使得$(u,v)\in T$，使得$(u,v)\in T$，使得$(u,v)\notin A$，并且$(u,v)$对于集合A是安全的。

Kruskal算法和Prim算法就是如何快速找到安全边的算法。

Kruskal算法

也称“加边法”，初始时，最小生成树集合里面包含所有顶点，但不包含任何边，每迭代一次就选择一条满足要求的边加入到集合里。

MST-KRUSKAL(G,w)
	A = Ø
	for each vertex v∈G.V
		MAKE-SET(v)
	sort the edges of G.E into nondecreasing orger by weight w	// 按升序对边进行排序
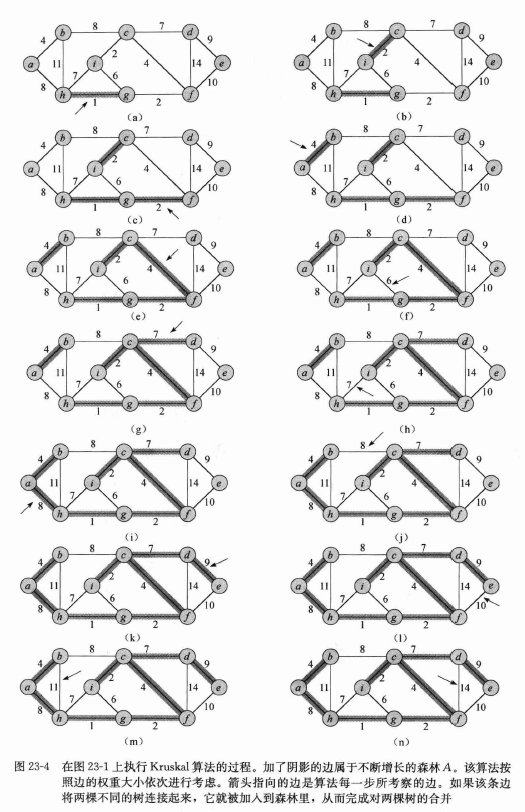
	for each edge(u,v)∈G.E, taken in nondecreasing order by weight
		if FIND-SET(u)≠FIND-SET(v)	// 判断结点u，v是否属于同一棵树
			A=A∪{(u,v)}
			UNION(u,v)	// 合并两棵树
	return A

1. 2~4行将集合A初始化为一个空集合，并创建$|V|$棵树，每棵树包含一个结点。
2. 5~9行的for循环按照权重从低到高的次序对每条边逐一进行检查。对于每条边$(u,v)$来说，该循环将检查端点u和端点v是否属于同一棵树。
   • 如果是，该条边不能加入到森林里，否则会形成环路；
   • 如果不是，两个端点分别属于不同的树，算法第8行将该条边加入集合A，第9行将两棵树中的结点进行合并。

运行时间

1. 第2行对集合A进行初始化：$O(1)$
2. 第5行对边进行排序：$O(E\lg E)$
3. 第6~9行的for循环，执行$O(E)$个FIND-SET和UNION操作以及$|V|$个MAKE-SET操作，总运行时间为：$O((V+E)\alpha (V))$

$\alpha$是定义的一个增长非常缓慢的函数，假定图G是连通的，则有$|E|\ge |V|-1$，所以不相交集合操作的时间代价为$O(E\alpha (V))$。而且，由于$\alpha (|V|)=O(\lg V)=O(\lg E)$，Kruskal算法的总运行时间为$O(E\lg E)$。

正确性证明

贪心选择性

只需证明每一步得到的边的集合，都是最小生成树的子集。

定理1

设$(u,v)$是G中权值最小的边，则必有一棵最小生成树包含边$(u,v)$

证明：

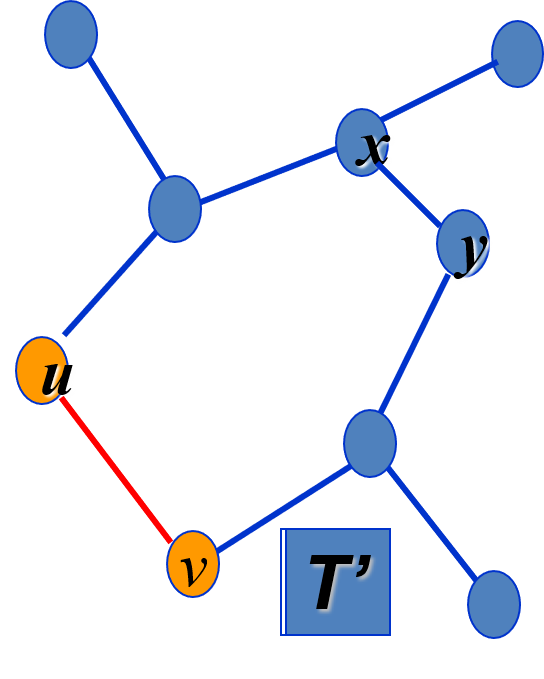
设T是G的一棵最小生成树，若$(u,v)\in T$，结论成立；

否则如图所示，在T中添加$(u,v)$边，产生环，删除环中不同于$(u,v)$的权值最小的边$(x,y)$，得到T’
$$w(T^{\prime })=w(T)-w(x,y)+w(u,v)\le w(T)$$
与假设中T为最小生成树矛盾

所以定理1成立

优化子结构

定理2

给定连通无向图$G=(V,E)$和权重函数$w:E\to R$，$(u,v)\in E$是G中权值最小的边。设T是G的包含$(u,v)$的一棵最小生成树，则$T-(u,v)$是$G-(u,v)$的一棵最小生成树。

证明：

由于$T-(u,v)$是不含回路的连通图且包含了$G-(u,v)$的所有顶点，因此，$T-(u,v)$是$G-(u,v)$的一棵生成树。

假设$T-(u,v)$不是$G-(u,v)$生成代价最小的一棵生成树，则存在$G-(u,v)$的生成树T’，使得$w(T^{\prime })<w(T-(u,v))$。

其中，T’包含顶点$G-(u,v)$且是连通的，因此$T^{\prime \prime }=T^{\prime }+(u,v)$包含G的所有顶点且不含回路，所以T’'是G的一棵生成树
$$w(T^{\prime \prime })=w(T^{\prime })+w(u,v)<w(T-(u,v))+w(u,v)=w(T)$$
与T是G的最小生成树的假设矛盾，所以定理2成立。

Prim算法

也称“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中， 算法从某一顶点开始，逐渐长大直到覆盖整个连通网的所有顶点。

连通图G和最小生成树的根结点r将作为算法的输入。算法执行过程中，所有不在树A中的结点都存放在一个基于key属性的最小优先队列Q中，对于每个结点v，属性v.key保存的是连接v和树中结点的所有边中最小边的权重，如果不存在这样的边，则v.key=∞。属性v.Π给出的是结点v在树中的父节点。Prim算法将GENERIC-MST中的集合A维持在
A={(v,v.π):v∈V−{r}−Q} A=\{(v,v.\pi):v\in V-\{r\}-Q\} A={(v,v.π):v∈V−{r}−Q}
的状态下。

当Prim算法终止时，最小优先队列Q将为空，而G的最小生成树A则是：
A={(v,v.π):v∈V−{r}} A=\{(v,v.\pi):v\in V-\{r\}\} A={(v,v.π):v∈V−{r}}

MST-PRIM(G,w,r)
	for each u∈G.V
        u:key=∞
        u:Π=NIL
	r:key=0
	Q=G.V
	while Q≠Ø
		u=EXTRACT-MIN(Q)
		for each v∈D.Adj[u]
			if v∈Q and w(u,v) < v.key
				v.Π=u
    			v.key=w(u,v)

1. 2~6行将每个结点的key值设置为∞（除根结点r外，根结点r的key值设置为0，以便使该结点成为第一个被处理的结点），将每个结点的父节点设置为NIL，并对最小优先队列Q进行初始化，使其包含图中所有结点。

2. 7~12行的每遍循环之前：

   1. A={(v,v.π):v∈V−{v}−Q}A=\{(v,v.\pi):v\in V-\{v\}-Q\}A={(v,v.π):v∈V−{v}−Q}
   2. 已经加入到最小生成树的结点为集合$V-Q$
   3. 对于所有的结点$v\in Q$，如果$v.\pi \ne NIL$，则$v.key<\infty$并且$v.key$是连接结点v和最小生成树中某个结点的边$(v,v.\pi )$的权重

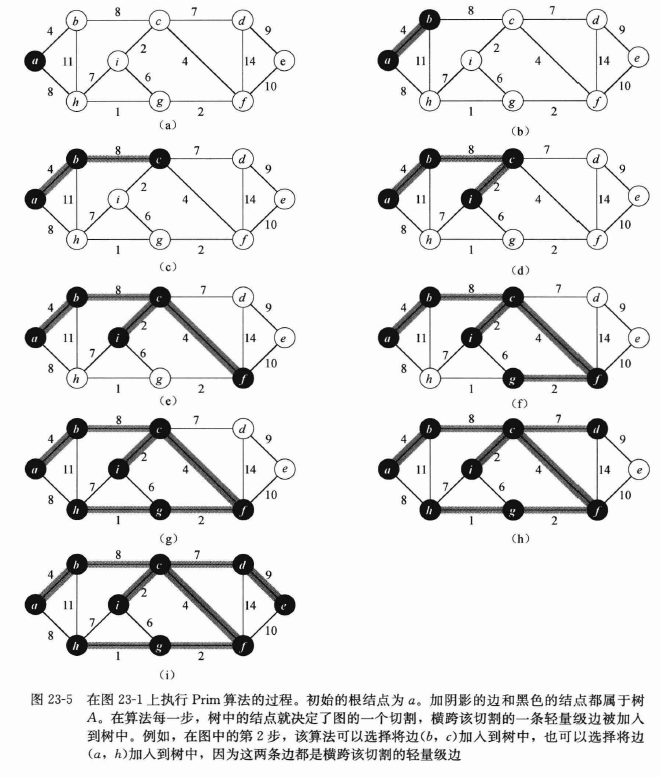
   算法第8行将找出结点$u\in Q$，该结点是某条横跨切割$(V-Q,Q)$的轻量级边的一个端点（第1次循环时例外，此时因为算法第5行，所以有u=r）。接着将结点u从队列Q中删除，并将其加入到集合V-Q中，也就是将边$(u,u.\pi )$加入到集合A中。

   9~12行的for循环将每个与u邻接但不在树中的结点v的key和Π值进行更新，从而维持循环不变式的第3部分成立。

运行时间

Prim算法的运行时间取决于最小优先队列Q的实现方式。

1. while循环：一共执行$|V|$次
2. **EXTRACT-MIN操作：**单次操作$O(\lg V)$，总时间为$O(V\lg V)$
3. for循环：$O(E)$

总时间代价为：
$$O(V\lg V+E\lg V)=O(E\lg V)$$
从渐进意义上来说，Prim算法与Kruskal算法的运行时间相同。

算法正确性

贪心选择性

定理3

设$(u,v)$是G中与顶点u关联的权值最小的边，则必有一棵最小生成树包含边$(u,v)$

证明：

设T是G的一棵最小生成树，若$(u,v)\in T$，结论成立；

否则，如图所示，在T中添加$(u,v)$边，产生环，环中顶点u的度为2，即存在$(u,v^{\prime })\in T$，删除环中的边$(u,v^{\prime })$得到T’
$$w(T^{\prime })=w(T)-w(u,v^{\prime })+w(u,v)\le w(T)$$
与T为最小生成树的假设矛盾，所以定理3成立。

最优子结构

与Kruskal算法最优子结构的证明相同。