数据结构-堆

文章中部分内容和思路来自《数据结构、算法与应用 c++语言描述》

预备知识

• 优先级队列：是0个或多个元素的集合，每个元素都有一个优先级或值，对优先级队列执行的操作有：1)查找一个元素 2)插入一个新元素 3)删除一个元素，与这些操作相对应的函数是top,push和pop。在最小优先级队列中，查找和删除的元素都是优先级最小的元素；在最大优先级队列中，查找和删除的元素都是优先级最大的元素。优先级队列中的元素可以有相同优先级，这样的元素查找与删除顺序任意。
• 大根(小根树)：一棵大根(小根)树是这样一棵树，其中每个节点的值都大于(小于)或等于其子节点(如有)的值，如图：

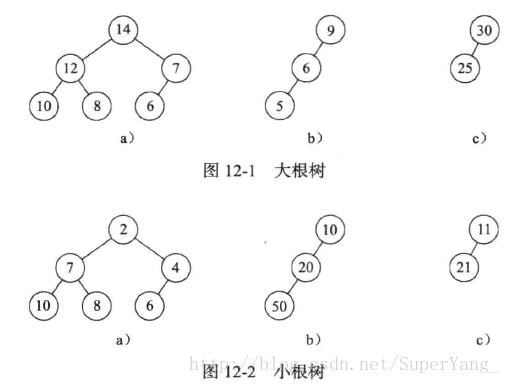
堆定义

堆主要分为大根堆和小根堆，大根(小根)堆既是大根(小根)树，也是完全二叉树。如12-1(b) 虽是大根树，但不是大根堆。[ps:后续内容皆以大根堆为例]

堆构建

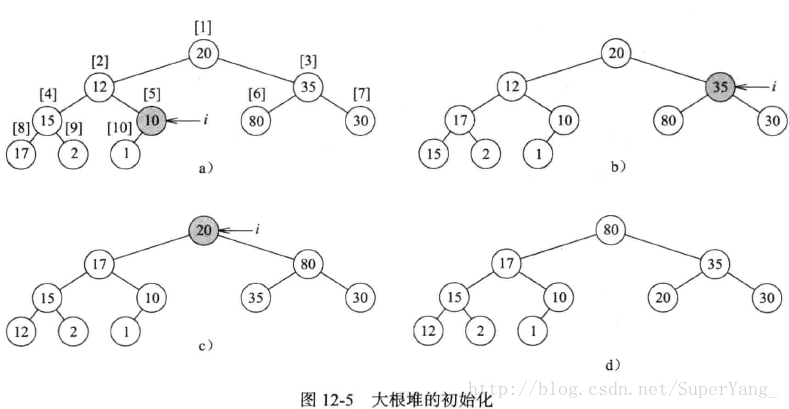
1.构建思路：将优先级数组构建成完全二叉树，再调整二叉树中各节点的位置。具体调整方法如图12-5，从最后一个有子树的节点开始将其调整成大根堆，如图12-5(a)中的[5]，已经是大根堆，则不再调整；然后调整[4]节点，15<17则调换位置，如图12-5(b)，以同样的方式调整3-2-1节点即可。

2.代码实现

template<typename T>

MaxHeap<T>::MaxHeap(T *arr, uint size)

{

    _heap = new T[size];

    memset(_heap, 0, sizeof(T) * size);

    memcpy(_heap, arr, sizeof(T) * size);

    _size = size;

    // 构建大根堆

    for (uint i = _size / 2 - 1; i >= 0; i--)

    {

        if (i == 0xffffffff)

            return;

        T rootEle = _heap[i];

        uint childIndex = 2 * i + 1;

        while(childIndex <= _size - 1)

        {

            if (childIndex < _size - 1 && _heap[childIndex] < _heap[childIndex + 1]) // 找到左右子节点中的大值

                childIndex++;

            // 已经符合大根堆

            if (rootEle >= _heap[childIndex])

                break;

            _heap[(childIndex - 1) / 2] = _heap[childIndex]; // 孩子上移

            childIndex = childIndex * 2 + 1; // 移到下一层

        }

        _heap[(childIndex - 1) / 2] = rootEle;

    }

}

堆插入

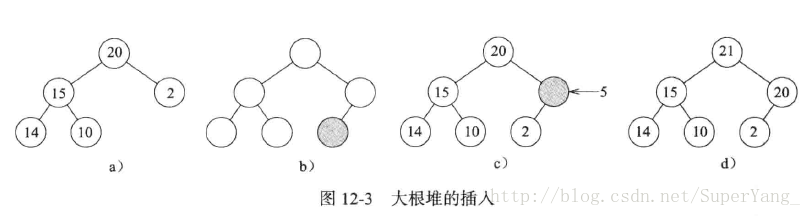
1.插入思路：把新元素插入到新节点，然后沿着从新节点到根节点的路径，执行一趟冒泡操作，将新元素与其父节点比较，直到后者大于或者等于前者为止[即先插入，再调整位置]。如插入数字1，插入后与其父节点比较大小，满足条件则不需要调整为止，如图12-3(b)所示。(c)、(d)图中分别插入5、21，图(c)执行一次调整位置，图(d)执行两次调整位置。

2.代码实现：

template<typename T>

void MaxHeap<T>::push(const T &node)

{

    T *newBlock = new T[_size + 1];

    memset(newBlock, 0, sizeof(T) * (_size + 1));

    memcpy(newBlock, _heap, sizeof(T) * _size);

    if (_heap)

    {

        delete []_heap;

        _heap = NULL;

    }

    _heap = newBlock;

    _size++;

    _heap[_size - 1] = node; // 增加新节点

    int nodeIndex = 0;

    for (nodeIndex = _size - 1; nodeIndex != 0 && _heap[(nodeIndex - 1) / 2] < node; nodeIndex /= 2)

    {

        _heap[nodeIndex] = _heap[(nodeIndex - 1) / 2];

    }

    _heap[nodeIndex] = node;

}

堆删除

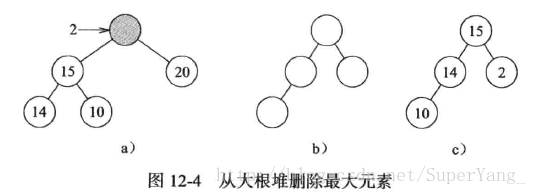
1.删除思路：首先删除根元素[只删除值保留节点]，然后删除最小叶子节点[取出值删除节点]，最后调整节点顺序。如12-3(d)中删除一个元素，则如图(a)[根节点为20,20的节点填2]

2.代码实现

template<typename T>

void MaxHeap<T>::pop()

{

    if (0 == _size)

        return;

    T rootEle = _heap[_size - 1];

    uint nodeIndex = 0;

    uint childIndex = 2 * nodeIndex + 1;

    while(childIndex <= _size - 1)

    {

        if (childIndex < _size - 1 && _heap[childIndex] < _heap[childIndex + 1]) // 找到左右子节点中的大值

            childIndex++;

        // 已经符合大根堆

        if (rootEle >= _heap[childIndex])

            break;

        _heap[(childIndex - 1) / 2] = _heap[childIndex]; // 孩子上移

        nodeIndex = childIndex;

        childIndex = childIndex * 2 + 1; // 移到下一层

    }

    _heap[nodeIndex] = rootEle;

    T *newBlock = new T[_size - 1];

    memset(newBlock, 0, sizeof(T) * (_size - 1));

    memcpy(newBlock, _heap, sizeof(T) * (_size - 1));

    if (_heap)

    {

        delete []_heap;

        _heap = NULL;

    }

    _heap = newBlock;

    _size--;

}

 ====================================================================

博主有自己的个人主页啦！请求关注，请求支持。QAQ.