python基础教学day15--数据结构与算法_数据结构 python 教学计划-优快云博客

本文链接：https://blog.youkuaiyun.com/Successful_clown/article/details/96423964

本文介绍了算法的基础概念，包括算法的定义、特性及效率衡量方式，并详细解释了时间复杂度的概念及其计算规则。同时，文章还探讨了顺序表与链表这两种基本数据结构的原理与实现方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、导论

1、算法引入

1.1 算法是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。
1.2 算法的五大特征

输入：有0个或多个输入
输出：至少有一个或者多个输出
有穷性：有限的步骤之后会自动结束
确定性：每一步都有确定的含义
可行性：每一步都是可行的
算法的时间复杂度一般都是最坏时间复杂度

2、算法效率衡量

2.1 执行时间反应算法效率内容
实现算法程序的执行时间可以反映出算法的效率，即算法的优劣。
2.2程序的运行离不开计算机环境(包括硬件和操作系统)，单纯依靠运行的时间来比较算法的优劣并不一定是客观准确的！
2.3 时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n))，则称O(g(n))为算法A的近似时间复杂度，简称时间复杂度，记为T(n)
**2.4 **“大O记法”:计量算法操作数量的规模函数中那些常量因子可以忽略不计
2.5时间复杂度计算规则

基本操作：只有常量，认为时间复杂度为ieO（1）
顺序结构：时间复杂度按加法进行计算
循环结构：时间复杂度按乘法进行计算
分支结构：时间复杂度取最大值

3、算法分析

时间复杂度计算对比

for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a**2 + b**2 == c**2 and a+b+c == 1000:
                print("a,b,c:%d,%d,%d"%(a,b,c))
                #时间复杂度为：T（n）=O(n*n*n)=O(n^3)

for a in range(0,1001):
    for b in range(0,1001):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a,b,c:%d,%d,%d" % (a, b, c))
            #时间复杂度为O(n^2)

4、时间复杂度

从上到下效率依次递减

大O表示法	术语
O(1)	常数阶
O(logn)	对数阶
O(n)	线性阶
O(n*logn)	nlogn阶
O(n²)	平方阶
O(n)³	立方阶
O(2ⁿ)	指数阶
O(n!)	阶乘阶

5、性能分析

1.1、
class timeit.Timer(stmt=‘pass’, setup=‘pass’, timer=)

Timer是测量小段代码执行速度的类
stmt参数是要测试的代码语句
setup参数是运行代码时需要的设置
timer参数是一个定时器函数，与平台无关。

timeit.Timer.timeit(number=1000000)

测试语句执行速度的对象方法
number参数测试代码时的测试次数，默认为1000000次。

def test1():
    I = []
    for i in range(1000):
        I = I + [i]
def test2():
    I = []
    for i in range(1000):
        I.append(i)
def test3():
    I = [i for i in range(1000)]
def test4():
    I = list(range(1000))

if __name__=="__main__":
    from timeit import Timer
    t1 = Timer('test1()','from __main__ import test1')
    print('concat',t1.timeit(number=1000),'seconds')
    t2 = Timer('test2()','from __main__ import test2')
    print('append',t2.timeit(number=1000),'seconds')
    t3 = Timer('test3()','from __main__ import test3')
    print('comprehension',t3.timeit(number=1000),'seconds')
    t4 = Timer('test4()','from __main__ import test4')
    print('list range',t4.timeit(number=1000),'seconds')
    x = list(range(100))
    pop_zero = Timer('x.pop(0)','from __main__ import x')
    print('pop__zero',pop_zero.timeit(number=1000),"seconds")
    x = list(range(100))
    pop_end = Timer('x.pop()','from __main__ import x')
    print('pop_end',pop_end.timeit(number=1000),"seconds")

二、顺序表

1、数据结构

**1.1、**数据的逻辑结构

线性结构：线性表、栈、队列
非线性结构：树、图

**1.2、**数据的存储结构

顺序结构
链式存储
索引存储
散列存储

**1.3、**数据的运算

检索、排序、插入、删除、修改等

python提供现成的数据结构类型叫做python的内置数据结构，比如列表、元组、集合、字典。
python系统里面没有=直接定义需要自定义的称为python的扩展数据结构，比如栈、队列等

2、顺序表的基本形式

**2.1、**顺序表，将元素顺序地存放在一块连续的存储区里，元素间顺序关系由它们的存储顺序自然表示

3、顺序表的结构与实现

**3.1、**一个完整信息包括两部分：

表中的元素集合
表的整体情况的信息：元素存储区的容量和元素个数。
**3.2、**图a为一体式结构，存储表信息的单元与元素存储区以连续的方式安排在一块存储区里。
图b为分离式结构，存储表信息的单元与元素存储区以连续的方式安排在两块存储区里。
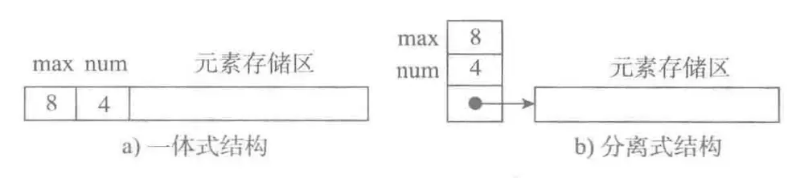
一体式结构：若想要更换数据区，则只能整个搬迁，即整个顺序表对象改变了。
分离式结构：若想更换数据区，只需将表中信息区的数据区链接地址更新即可，而该顺序表对象不变。

**3.3、**只有分离式结构的元素存储区可以扩充。
扩充的两种策略：

每次扩充增加固定数目的存储位置，如每次扩充增加10个元素位置，这种策略可称为线性增长。特点：节省空间，但是扩充操作频繁，操作次数多。
每次扩充容量加倍，如每次扩充增加一倍存储空间。**特点：**减少了扩充操作的执行次数，但可能会浪费空间资源，以空间换时间，推荐的方式。

4、顺序表的操作

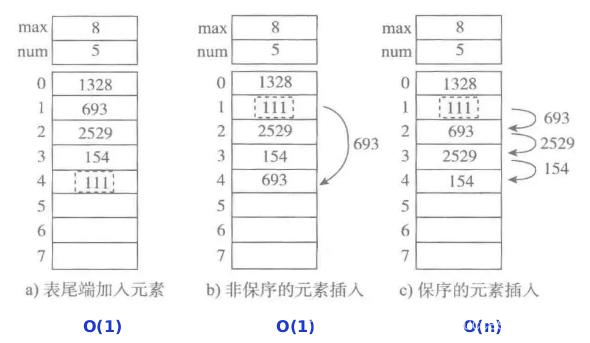
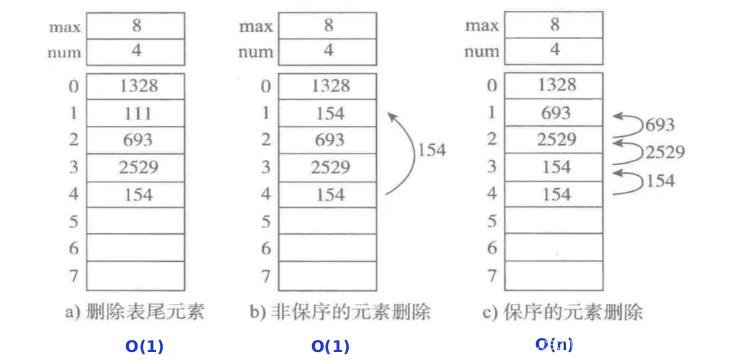
在这里插入图片描述

5、python中的顺序表

**5.1、**python中的list和tuple两种类型采用了顺序表的实现技术。

list是可变类型，即采用分离式技术实现的动态顺序表
tuple是不可变类型，即不变的顺序表；

**5.2、**python标准类型list就是一种元素个数可变的线性表，可以加入和删除元素，具有以下特征；

顺序表：基于下标的高效元素访问和更新，时间复杂度是O(1)；
分离式技术：允许任意加入元素，而且在不断加入元素的过程中，表对象的标示(id)不变

5.3、

在建立空表时，系统分配一块能容纳8个元素的存储区；
在执行插入操作时，如果元素存储区满就换一块4倍大的存储区。
如果此时的表已经很大，则改变策略，采用加一倍的方法。原因：为了避免出现过多的存储位置。

三、链表

1、链表

**1.1、**顺序表的构建需要预先知道数据大小申请连续的存储空间，而在进行空充时又需要进行数据的搬迁，所以使用起来并不是很灵活。
链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理.
1.2 链表是一种常见的基础数据结构,是一只种类线性表,但是不像顺序表一样连续存储数据,而是在每一个节点(数据存储单元)里存放下一个节点的位置信息.

2.单链表

2.1. 单向链表也叫单链表，每个节点包含两个域，一个信息域（元素域）和一个链接域。这个链接指向链表中的下一个节点，而最后一个节点的链接域则指向一个空值。
2.2.
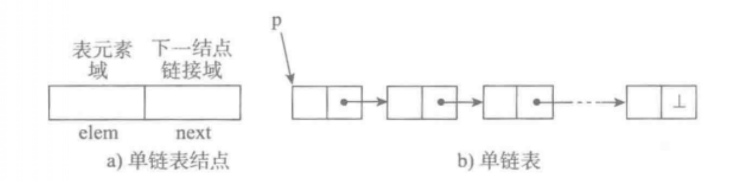
在这里插入图片描述

表元素域elem用来存放具体的数据。
链接域next用来存放下一个节点的位置（python中的标识）
变量p指向链表的头节点（首节点）的位置，从p出发能找到表中的任意节点。

代码实现

class Node(object):
    """
    单链表节点的封装

    """
    def __init__(self,element):
        self.element = element
        self.next = None


class Singlelink(object):
    def __init__(self):
        #默认情况下链表为空，没有任何元素
        self.head = None

    def is_empty(self):
        '''
        判断链表是否为空
        :return:
        '''
        return self.head == None
    def __len__(self):
        """链表长度"""
        if self.is_empty():
            return 0
        else:
            cur = self.head
            length = 0
            while cur != None:
                length += 1
                cur = cur.next
            return length

    def trvel(self):
        """遍历链表"""
        if not self.is_empty():
            cur = self.head
            while cur.next != None:
                print(cur.element,end=',')
                cur = cur.next
            print(cur.element)
        else:
            print('空链表')
    def append(self,item):
        """尾部添加元素
        1、先判断链表是否为空，若是空链表，则将head指向新的节点
        2、若不为空，则找到尾部，将尾节点的next指向新节点
        """
        node = Node(item)
        if self.is_empty():
            self.head = node
        else:
            cur = self.head
            while cur.next != None:
                cur = cur.next
            cur.next = node
    def add(self,item):
        """头部添加元素
        1、先创建一个保存item值的节点
        2、将新节点的链接域next指向头节点，即head指向的位置
        3、将链表的头head指向新节点"""
        node = Node(item)
        node.next = self.head
        self.head = node
    def insert(self,index,item):
        """
        指定位置添加元素
        1、若指定位置index为第一个元素之前，则执行头部插入
        2、若指定位置超过链表尾部，则执行尾部插入
        3、否则，找到指定位置
        :param index:
        :param item:
        :return:
        """
        if index <= 0:
            self.add(item)
        elif index >= len(self):
            self.append(item)
        else:
            node = Node(item)
            count = 0
            cur = self.head
            while count < index -1:
                count += 1
                cur = cur.next
            node.next = cur.next
            cur.next = node
    def move(self,index,item):
        """
        移动
        1、

        :param item:
        :return:
        """
        node = Node(item)
        cur = self.head
        count = 0
        while count != index:
            cur = cur.next
            count += 1
        cur.next = node
if __name__ == '__main__':
    link = Singlelink()
    #长度获取
    print(len(link))
    #链表遍历
    link.trvel()
    print('添加元素：')
    link.append(1)
    link.append(2)
    link.add(3)#在链表的头部添加
    link.insert(1,'chen')
    # 长度获取
    print(len(link))
    # 链表遍历
    link.trvel()
    link.move(2,3)
    link.trvel()