第5节机器学习--逻辑回归--评估指标

本文详细介绍了逻辑回归及其评估指标。从逻辑回归的sigmoid函数、损失函数到K折交叉验证，再到查准率、查全率、P-R曲线、F1 Score和ROC曲线，深入探讨了各种评估标准在二分类问题中的应用和意义，帮助理解模型的性能表现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、逻辑回归

1、有监督机器学习
线性回归：预测一个连续的值
逻辑回归：预测一个离散的值
例：阶跃函数：不连续的
2、
良性肿瘤 and 恶性肿瘤。
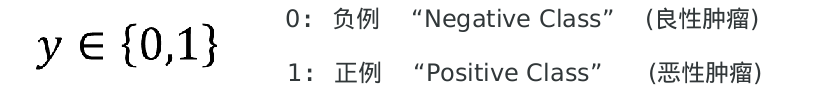
在这里插入图片描述
如果想要模型的y值坐落在[0,1]的区间上那么就需要使用sigmoid函数。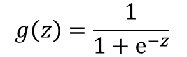

线性回归模型：
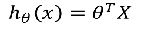
在这里插入图片描述
带入之后得：

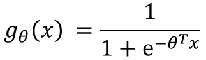
如果：

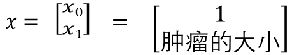
g（x） = 0.7

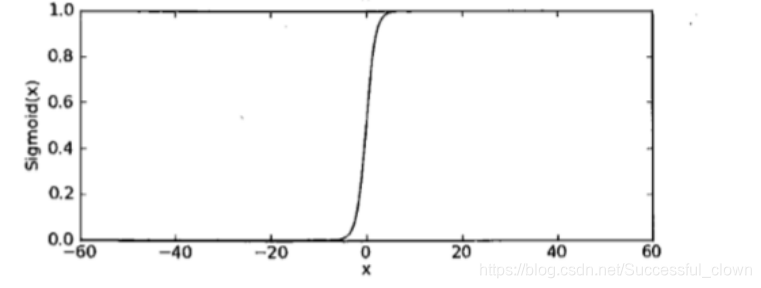
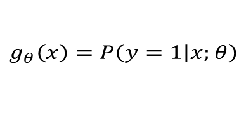
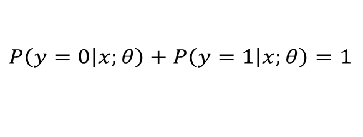
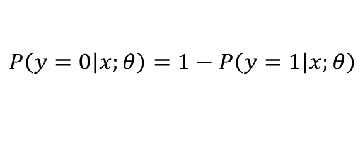
3、sigmoid函数的作用

数学上，是根据广义线性回归的模型推导所得的结果。
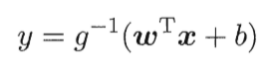
直观上，
（1）输出范围有限，数据在传递中不容易发散
（2）抑制两头，对中间细微变化敏感，对分类有利
（3）性质优秀，方便使用（Sigmoid函数是平滑的，而且任意阶可到，一阶二阶导数可以直接由函数得到，不用求导，这在做梯度下降的时候很实用。

4、怎样解决比线性和非线性的决策边界？
训练集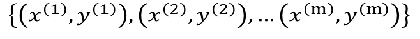：在这里插入图片描述
样本：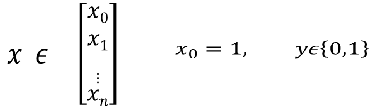

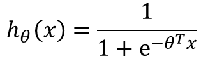
怎样选择θ?
线性回归的方法是：损失函数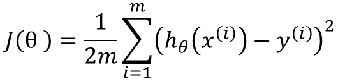
引入熵，熵的意义：热力学上：熵是一种测量分子不稳定的指标，分子运动越不稳定，熵就越大
信息论（香农）：熵是一种测量信息量的单位，信息熵，包含的信息越多，熵就越大。
机器学习:熵是一种测量不确定性的单位，不确定性越大，概率越小，熵就越大！
注：信息量：越不可能发生的事情发发生了，我们获取的信息量就越大。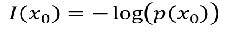在这里插入图片描述
熵：表示所有信息量的期望。

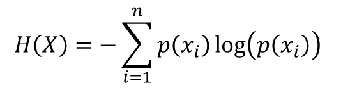
交叉熵：用来衡量两个样本分布差异的，也可以说是用来衡量两个样本的相似性
在机器学习中，P往往用来表示样本的真实分布，Q用来表示模型所预测的分布。

逻辑回归的损失函数与线性回归相似！
4、SolfMax回归
有一种逻辑回归的一般形式，叫做Softmax回归，能让你在试图识别某一分类中做出预测，或者说多分类的一种，不只是识别两个分类。
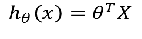
在这里插入图片描述
然后在做非线性变化的时候：不用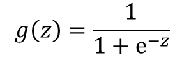
取而代之的是：

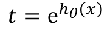
对于t求和：

然后每个特征处于总和：

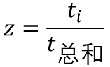
逻辑回归与SoftMax的区别
逻辑回归主要是用来做二分类的
Softmax主要是用来做多分类的；SoftMax回归将logistic激活函数推广到C类，而不仅仅是两类，如果C=2，那么softmax实际上就是逻辑回归
例1: 项目音乐分类器

#encoding:utf-8
"""
基于快速傅立叶变化的音乐分类器
"""
# 用来读取wav格式的音乐数据
import numpy as np
from scipy.io import wavfile
# 用来做快速傅立叶变化
from scipy import fft
from sklearn.linear_model import LogisticRegression
from tqdm import tqdm


# 准备音乐数据
def create_fit(g, n):
    """

    :param g: 音乐的分类
    :param n: 音乐的索引序数
    :return:
    """
    # zifll返回制定长度的字符串，原字符串右对其，前面填充0
    rad