1 间隔与支持向量机
分类学习最基本的想法就是基于训练集在样本空间找到一个划分超平面,将不同类别的样本分开。划分超平面可以通过如下的线性方程来描述:
其中 为法向量,决定了超平面的方向;
为法向量,决定了超平面的方向; 为位移项,决定了超平面和原点之间的距离。样本空间中任意点
为位移项,决定了超平面和原点之间的距离。样本空间中任意点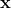 到超平面
到超平面 的距离可写为:
的距离可写为:
令
如下图使得(3)等号成立的距离超平面最近的这几个训练样本点称为“支持向量”(support vector),两个异类支持向量到超平面的距离之和为
其被称为间隔(margin)

欲找到具有最大间隔的划分超平面,也就是要找到满足(3)式的参数 和
和 ,使得
,使得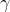 最大,即
最大,即
显然,为了最大化间隔,仅需最大化 ,这等价于最小化
,这等价于最小化 ,于是(5)可重写为:
,于是(5)可重写为:
 (6)
(6)这就是支持向量机(support vector machine, SVM)的基本型。
2 对偶问题
通过上述描述 我们想要通过(6)来得到最大间隔划分超平面所对应的模型
 (7)
(7)(6)式本身是一个凸二次规划(convex quadratic programming)问题,能直接用现成的优化计算包求解,但是可以用更高效的办法。
整个思路:为确定函数 中的参数
中的参数 和
和 ,寻找最大分类间隔,导出
,寻找最大分类间隔,导出 ,继而引入拉入拉格朗日函数,化为单一因子对偶变量
,继而引入拉入拉格朗日函数,化为单一因子对偶变量 的求解,如此,求
的求解,如此,求 与
与 等价,而求
等价,而求 即为SMO。
即为SMO。
 中的参数
中的参数对式(6)使用拉格朗日乘子法可得到其“对偶问题”(dual problem):
其中 。令
。令 对
对 和
和 的偏导为零可得:
的偏导为零可得:
 (9)
(9)将(9)带入(8)再考虑(10)的约束,就得到了(6)的对偶问题:
 (11)
(11)求解 后即可得到模型:
后即可得到模型:
 (12)
(12)上述过程需满足KKT(Karush-Kuhn-Tucker)条件,即要求:
若 ,则
,则 ,所对应的样本点位于最大间隔边界上,是一个支持向量,这显示出支持向量的一个重要性质:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
,所对应的样本点位于最大间隔边界上,是一个支持向量,这显示出支持向量的一个重要性质:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
(11)是一个二次规划问题,采用二次规划算法求解时,当训练样本较多时,开销很大。因此,采用SMO(Sequential Minimal Optimization)的高效算法。
SMO的基本思路是先固定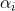 之外的所有参数,然后求
之外的所有参数,然后求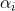 上的极值。由于存在约束
上的极值。由于存在约束 ,若固定
,若固定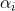 外的其他变量,则
外的其他变量,则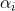 可由其他变量导出。于是SMO每次选择两个变量
可由其他变量导出。于是SMO每次选择两个变量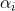 和
和 ,并固定其他参数,这样,在参数初始化时,SMO不断执行如下两个步骤直至收敛:
,并固定其他参数,这样,在参数初始化时,SMO不断执行如下两个步骤直至收敛:
1)选取一对需要更新的变量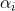 和
和 ;
;
2)固定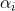 和
和 以外的参数,求解(11)获得更新后的
以外的参数,求解(11)获得更新后的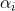 和
和
选择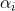 和
和 时,选取的两变量所对应的样本之间的间隔最大,直观的解释就是:这样的两个变量有很大的差别,对它们进行更新会给目标函数更大的变化。
时,选取的两变量所对应的样本之间的间隔最大,直观的解释就是:这样的两个变量有很大的差别,对它们进行更新会给目标函数更大的变化。
仅考虑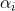 和
和 时,(11)中的约束条件可重写为:
时,(11)中的约束条件可重写为:
其中
用(14)中的等式消去(11)中的 ,则得到一个关于变量
,则得到一个关于变量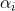 的单变量二次规划问题,仅有的约束为
的单变量二次规划问题,仅有的约束为 ,这样的二次规划问题是有闭式解的,不必调用优化算法即可高效的计算出更新后的
,这样的二次规划问题是有闭式解的,不必调用优化算法即可高效的计算出更新后的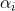 和
和 。
。
然后就是确定偏移项 ,主要到对支持向量
,主要到对支持向量 ,都有
,都有 ,即
,即
其中 为所有支持向量的下标集。理论上可选取任意支持向量机并通过求解(16)式获得b,但现实任务中常采用一种鲁棒性的做做法:使用所有支持向量求解的平均值
为所有支持向量的下标集。理论上可选取任意支持向量机并通过求解(16)式获得b,但现实任务中常采用一种鲁棒性的做做法:使用所有支持向量求解的平均值
3 核函数
前边的讨论中样本是线性可分的,即存在一个划分超平面能将训练样本正确分类,然而在现实任务中,原始样本空间内也许并不存在一个能正确划分两类样本的超平面,对这样的问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。幸运的是,若原始空间是有限维的,即属性数有限,那么一定存在一个高维的特征空间使样本可分。
令 表示
表示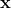 映射后的特征向量,于是在特征空间中划分超平面所对应的模型可表示为:
映射后的特征向量,于是在特征空间中划分超平面所对应的模型可表示为:
类似(6),有
其对偶问题为
求解(20)涉及到计算 ,这是样本
,这是样本 和
和 映射到高维特征空间之后的内积,通常直接计算
映射到高维特征空间之后的内积,通常直接计算 是比较困难的,为避开这样,可以设想一个函数:
是比较困难的,为避开这样,可以设想一个函数:
即 和
和 在特征空间的内积等于它们在原始样本空间中通过函数
在特征空间的内积等于它们在原始样本空间中通过函数 (核函数)计算的结果。于是(20)可重写为:
(核函数)计算的结果。于是(20)可重写为:
 (22)
(22)求解后可得到:
核函数的存在问题:
Mercer定理:
如果函数K是 上的映射(也就是从两个n维向量映射到实数域)。那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例
上的映射(也就是从两个n维向量映射到实数域)。那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例![clip_image065[7]](https://i-blog.csdnimg.cn/blog_migrate/cc32ab45551d370c8ca6c114b269caa5.png) ,其相应的核函数矩阵是对称半正定的。
,其相应的核函数矩阵是对称半正定的。
 上的映射(也就是从两个n维向量映射到实数域)。那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例
上的映射(也就是从两个n维向量映射到实数域)。那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例![clip_image065[7]](https://i-blog.csdnimg.cn/blog_migrate/cc32ab45551d370c8ca6c114b269caa5.png) ,其相应的核函数矩阵是对称半正定的。
,其相应的核函数矩阵是对称半正定的。常用核函数:
1 线性核函数
2 多项式核
3 高斯核

4 拉普拉斯核
5 Sigmoid核
此外,还可以通过组合得到:
若 和
和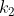 位核函数,
位核函数, 和
和 为任意正数,
为任意正数,
1)核函数的线性组合:
2)核函数的直积:
3)任意函数 :
:
4 软间隔与正则化
在现实任务中很难确定合适的核函数使得训练样例在特征空间线性可分;退一步说,即使恰好找到个某个核函数使训练样例在特征空间线性可分,也很难断定这个貌似线性可分的核函数是不是由于过拟合多造成的。
缓解该问题的一个办法是允许SVM在一些样本上出错,为此,要引入“软间隔”(soft margin )的概念。

前边所介绍的所有样本都必须划分正确,这成为“硬间隔”(hard margin),当引入软间隔时,就引入了松弛变量 ,在最大化间隔的同时,不满足约束样本应尽可能少,于是优化目标可写为:
,在最大化间隔的同时,不满足约束样本应尽可能少,于是优化目标可写为:
这就是“软间隔支持向量机”,其中C为惩罚因子。依据SVM的推到可得:

 (25)(其中的d相当于本文的y,敲公式太麻烦了,,,)
(25)(其中的d相当于本文的y,敲公式太麻烦了,,,)
























 1357
1357

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










