AcWing 860. 染色法判定二分图（染色法）

最新推荐文章于 2024-09-26 22:43:55 发布

原创最新推荐文章于 2024-09-26 22:43:55 发布 · 373 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#图论 #dfs

AcWing算法基础专栏收录该内容

78 篇文章

订阅专栏

本文介绍了一种基于深度优先搜索（DFS）的二分图判定算法。通过递归地为图中的每个节点染色，检查是否存在冲突来判断图是否可以被分为两组互不相连的节点集。适用于大规模图，数据范围可达10^5。

给定一个n个点m条边的无向图，图中可能存在重边和自环。

请你判断这个图是否是二分图。

输入格式

第一行包含两个整数n和m。

接下来m行，每行包含两个整数u和v，表示点u和点v之间存在一条边。

输出格式

如果给定图是二分图，则输出“Yes”，否则输出“No”。

数据范围

1≤n,m≤1051≤n,m≤105

输入样例：

输出样例：

Yes

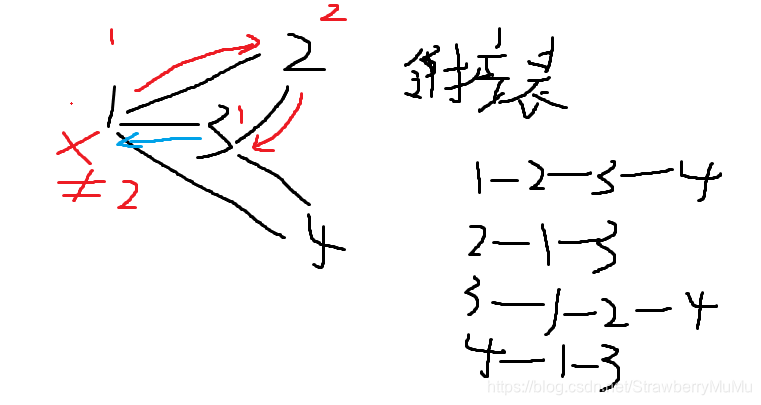
算法思想：

深搜，在搜索过程中不需要记录之前搜过的点，因为之前搜过的点可能还需要继续检查染色状态。


import java.io.*;
import java.lang.*;
import java.util.*;

class Main{
    static int n = 0, m = 0, N = 200010;
    static int[] e = new int[N], ne = new int[N], h = new int[N];
    static int idx = 1;
    static int[] color = new int[N];
    static void add(int a, int b){
        e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
    }
    
    static boolean dfs(int a, int c){
        color[a] = c;
        for(int i = h[a]; i != -1; i = ne[i]){
            int j = e[i];
            if(color[j] == 0){//未染色
                if(!dfs(j, 3 - c))return false;//深搜
            }else if(color[j] == c){//已经染色，但是染色不对
                return false;
            }
        }
        return true;
    }
    public static void main(String[] args)throws Exception{
        BufferedReader buf = new BufferedReader(new InputStreamReader(System.in));
        String[] params = buf.readLine().split(" ");
        n = Integer.valueOf(params[0]);
        m = Integer.valueOf(params[1]);
        Arrays.fill(h, -1);
        for(int i = 1; i <= m; ++i){
            String[] info = buf.readLine().split(" ");
            int a = Integer.valueOf(info[0]);
            int b = Integer.valueOf(info[1]);
            add(a, b);add(b, a);
        }
        
        for(int i = 1; i <= n; ++i){
            if(color[i] == 0)
                if(!dfs(i, 1)){
                    System.out.print("No");
                    return;
                }
            }
        System.out.print("Yes");
        
    }
}