台湾大学林轩田《机器学习基石》学习笔记第10讲—— Logistic Regression

最新推荐文章于 2020-10-10 17:42:51 发布

1021stones

最新推荐文章于 2020-10-10 17:42:51 发布

阅读量347

点赞数

CC 4.0 BY-SA版权

分类专栏：林轩田机器学习笔记文章标签： Machine Learning 机器学习基石林轩田学习笔记

本文链接：https://blog.youkuaiyun.com/Stoneeeee/article/details/82875270

林轩田机器学习笔记专栏收录该内容

16 篇文章

订阅专栏

本文详细探讨了Logistic Regression在二元分类问题中的应用，从风险分数到Sigmoid函数，解释了如何将线性模型转换为概率预测。接着，文章介绍了交叉熵误差作为Logistic Regression的错误度量，并通过梯度下降算法寻找最优解的过程。总结了基于梯度下降的Logistic Regression算法步骤，包括误差函数、梯度计算和迭代优化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、Logistic Regression Problem
在这里插入图片描述

仍然是心脏病预测的问题，可以根据病人的年龄、血压、体重等信息，来预测患者是否会有心脏病。这是一个二元分类问题，其输出y只有{-1,1}两种情况；
那么如果我们要预测的是病人患心脏病的概率是多少呢，这时候输出y就不是简单的{-1,1}了，而是区间[0,1]，我们把这个问题称为软性二分类问题（’soft’ binary classification）；

那么我们如何来找到一个hypothesis接近我们的目标函数f(x)∈[0,1]呢？
首先我们仍然对所有的feature进行加权处理，并得到s，我们称之为“risk score”；
但是特征加权和s∈(−∞,+∞)，如何将s值转化为在[0,1]之间呢？一个方法是使用Logistic Function，记为θ(s)，它的坐标图像如上；
于是我们就得到一个logistic hypothesis： $h(x)=θ(w^Tx)$ 。
θ(s)的解析式如上，它是一个平滑的、单调的“S型”函数。

二、Logistic Regression Error
首先，我们来看一下之前学过的另外两种linear model是如何来进行error measure：
在这里插入图片描述

三种model的scoring function一样都是 $s=w^Tx$ ；
不同的在于hypothesis是如何对s进行运算得到输出的，linear classification是公国sign(s)，linear regression直接输出s，而logistic regression则是通过sigmoid function θ(s);
前二者对应的error measure分别是0/1 error和squared error，那么针对logistic regression呢？
所谓的error measure就是对hypothesis h偏离target function f的衡量，换句话说就是h和f有多像，我们把这个叫做*“likelihood似然性”*，最像的那个g也叫做最大似然的likelihood；
考虑一个dataset D，他是由f产生的，那么其概率如左图，如果我们希望找到的那个最接近f的h存在，那么其也能产生同样的dataset D，其概率和f应该最接近；
因为f是我们认为实际产生D的，所以其概率是很大的，于是我们只要找到一个h使得likelihood(h)达到最大时，它就会是我们希望找到的g。
经过以上推导，我们得到likelihood(h)正比于h( $y_nx_n$ )的联乘，原因：
对于所有的h，P( $x_n$ )都是一样的，所以可以消除；
另外注意到这里的 $y_n$ 是正负类的输出，即{+1,-1}，而非区间[0,1]。

接下来我们队likelihood(h)在进行推导：

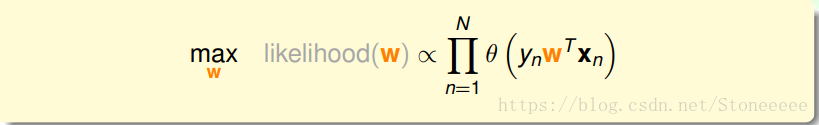
1.用w替代h()。

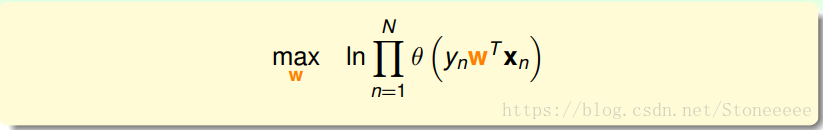
2.对联乘去log，这样可以把连乘去掉变成连加，方便计算最大值。

3.如下：
添加负号，把求最大值转化为求最小值，并引入平均数操作1/N；
带入θ(s)求得error function，我们把它称之为cross-entropy error交叉熵误差。

三、Gradient of Logistic Regression Error
上一小节中我们推到出了Ein,那么接下来就是找到一个w使得这个Ein越小越好。
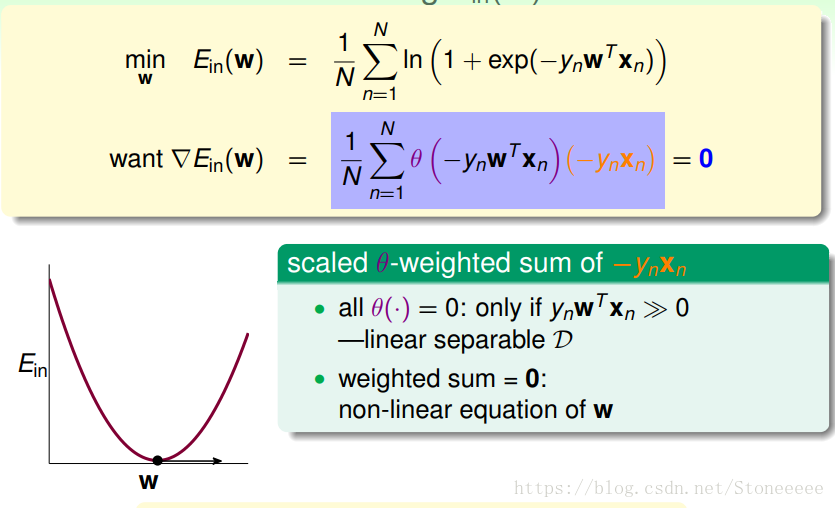
在这里插入图片描述

Logistic Regression的Ein是连续、可微、二次可微的凸曲线（开口向上），根据之前Linear Regression的思路，我们只要计算Ein的梯度为零时的w，即为最优解。
经过简单的微分计算，得到上图的Ein的偏微分梯度，注意到这里的 $x_n$ 是向量；
接下来就是计算这个梯度=0.
上式可以看成是θ和 $y_nx_n$ 的线性加权，θ是权重，那么我们就需要求得这个加权值等于0；
一种情况是当权重θ(·)全部都为0，即当 $y_nw^Tx_n≫0$ ，这样加权值就等于0，这种情况其实就是线性可分的，原因在于所有的 $y_n$ 要与 $w^Tx_n$ 同号；
但是大多数情况下，θ(·)全等于0并不现实，即非线性可分，只能通过求解整个加权值=0来求解w，但这通常没有closed-form解，但可以通过迭代的方式进行逼近求解。
以上前两步是我们之前学习过的PLA的修正过程；
我们对其进行整合得到下面的一个步骤；
w每次更新包含两个内容：一个是每次更新的方向ynxn，用v表示，另一个是每次更新的步长η；
参数(v,η)和终止条件决定了我们的迭代优化算法。

四、Gradient Descent
在这里插入图片描述

把上一小节中的Ein(w)想象成一个山谷，那么我们的目标就是尽快地到达谷底；
这里有两个参数：①v代表我们前进的方向；②μ则代表我们一步要走多远。
由于Ein(w)并不是线性的，但微积分告诉我们如果只考虑很小的一个单元，我们可以将其看成是线性的；
假设我们的μ取很小，经过Taylor一阶展开得到如上的式子。
因为式子中的 $E_{in}(w_t)$ 和μ都是常数，那么我们要求式子的最小值就需要想办法让第三项最小；
两个向量的内积要达到最小，那么就需要使他们方向相反，即v向量总是沿着 $E_{in}(w_t)$ 的反方向，因此推导得到以上的结果；
我们把这种算法叫做梯度下降（gradient descent）算法，理论上只要能求得梯度，那么这个算法就可以有效的执行。

接下来我们来考虑一下怎么来选择μ：
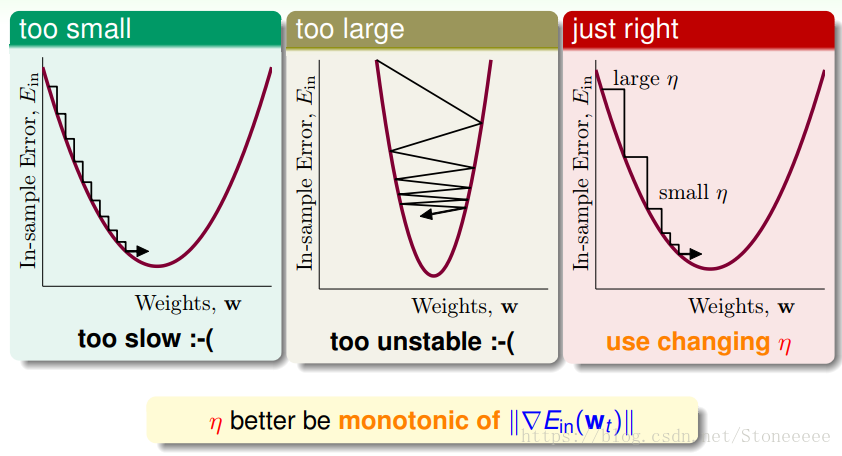
在这里插入图片描述

η如果太小的话，那么下降的速度就会很慢；
η如果太大的话，那么之前利用Taylor展开的方法就不准了，造成下降很不稳定，甚至会上升。
因此，η应该选择合适的值，一种方法是在梯度较小的时候，选择小的η，梯度较大的时候，选择大的η，即η正比于|| $E_{in}(w_t)$ ||。这样保证了能够快速、稳定地得到最小值Ein(w)。
这里注意到紫色μ其实是红色μ与|| $E_{in}(w_t)$ ||的比值，我们统一使用这个新的μ来表征式子中的两个项的比值，对其进行化简；
我们把这个紫色的μ称作为fixed learning rate 学习速度。

总结一下基于梯度下降的Logistic Regression算法步骤如下：
初始化 $w_0$
计算梯度 $E_{in}(w_t)$
迭代更新 $w_{t+1}←w_t−η▽E_{in}(w_t)$
迭代直至满足 $E_{in}(w_{t+1})≈0$

五、Summary
这节课主要介绍了Logistic Regression。首先从问题出发，将P(+1|x)作为目标函数，将θ(w)作为hypothesis。我们定义了logistic regression的err function，称之为cross-entropy error交叉熵误差。然后我们计算logistic regression error的梯度，最后通过梯度下降算法，经过数次迭代找到Ein最小时对应的 $w_t$ 。