仓颉编程语言-并发编程

一、并发编程概述

        并发是只多个任务在重叠的时间段内执行，可能通过时间片轮转、多核并行或异步调度实现。仓颉编程语言提供抢占式的线程模型作为并发编程机制，仓颉线程本质上是用户态的轻量级线程，每个仓颉线程都受到底层 native 线程的调度执行，并且多个仓颉线程可以由一个 native 线程执行。

二、创建线程

1.仓颉创建线程的关键字为spawn,语法为：spawn{主体}。

main(): Int64 {
    spawn {
        println("子线程")
        var a = 1
        var b = 2
        println(a+b)
    }
    sleep(Duration.second)
    println("主线程")
    return 0
}

结果为：

        上述代码中，用spawn表达式创建了一个线程，在该线程中执行一个加法运算，并在主线程内用sleep()方法进行睡眠，等待子线程运行完毕后再运行主线程。

2.spawn表达式返回值

        spawn表达式的返回值是Future<T>，当调用Future<T>的get()成员函数时，将等待线程执行完成。

main(): Int64 {
    let fu : Future<Unit> = spawn {
        println("子线程")
        var a = 1
        var b = 2
        println(a+b)
    }
    fu.get()
    println("主线程")
    return 0
}

结果为：

        用Future<T>的成员函数get()后会等待线程执行完成，在结果中体现为先出现的子线程和3，再出现的时主线程。

        当把fu.get()放在主线程后：

main(): Int64 {
    let fu : Future<Unit> = spawn {
        println("子线程")
        var a = 1
        var b = 2
        println(a+b)
    }
    println("主线程")
    fu.get()
    return 0
}

结果为：

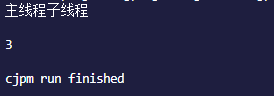
根据结果，打印的顺序则会变得不不固定。

三、同步机制

        在并发编程中，如果缺少同步机制来保护多个线程共享的变量，很容易出现数据竞争问题。因此可以用原子操作、互斥锁来解决。创建2000个线程，并用一个计数变量count来举例。

import std.collection.*
var count = 0
main(): Int64 {
    var lists : ArrayList<Future<Unit>> = ArrayList<Future<Unit>>()
    for(i in 0..2000)
    {
        let fu = spawn {
            count++
        }
        lists.append(fu)
    }
    for(item in lists)
    {
        item.get()
    }
    println("2000个线程count次数为:${count}")
    return 0
}

结果为：

        有结果可见，2000个线程理论上count的次数应该为2000，但是结果却显示为1992，出现了多个线程之间相互竞争从而出现了数据错误。以下方法可以解决：

1.原子操作

        使用原子操作需要导入包：import std.sync.AtomicInt64

import std.sync.AtomicInt64
import std.collection.*
var count = AtomicInt64(0)
main(): Int64 {
    var lists : ArrayList<Future<Int64>> = ArrayList<Future<Int64>>()
    for(i in 0..2000)
    {
        let fu = spawn {
            count.fetchAdd(1)
        }
        lists.append(fu)
    }
    for(item in lists)
    {
        item.get()
    }
    println("2000个线程count次数为:${count.load()}")
    return 0
}

结果为：

由结果可见，通过原子操作，便不会出现线程之间相互竞争而造成数据不安全的情况。

2.可重入锁（明锁）

        使用可重入锁需要导入包：import std.sync.ReentrantMutex

import std.sync.ReentrantMutex
import std.collection.*
var count = 0
let lock = ReentrantMutex()
main(): Int64 {
    var lists : ArrayList<Future<Unit>> = ArrayList<Future<Unit>>()
    for(i in 0..2000)
    {
        let fu = spawn {
            lock.lock()
            count++
            lock.unlock()
        }
        lists.append(fu)
    }
    for(item in lists)
    {
        item.get()
    }
    println("2000个线程count次数为:${count}")
    return 0
}

结果为：

由结果得，也得出了正确的结果。

注：明锁需要手动上锁并且手动解锁，分别用到lock()方法，和unlock()方法。

3.可重入锁（暗锁）

        使用暗锁同样需要导入包：import std.sync.ReentrantMutex，同时需要用到关键字synchronized。

import std.sync.ReentrantMutex
import std.collection.*
var count = 0
let lock = ReentrantMutex()
main(): Int64 {
    var lists : ArrayList<Future<Unit>> = ArrayList<Future<Unit>>()
    for(i in 0..2000)
    {
        let fu = spawn {
            synchronized(lock)
            {
                count++
            }
        }
        lists.append(fu)
    }
    for(item in lists)
    {
        item.get()
    }
    println("2000个线程count次数为:${count}")
    return 0
}

结果为：

综上：原子操作，可重入锁的明锁和暗锁机制都可以保证数据不会被线程竞争导致不安全。