人工智能概念之十：人工神经网络（ANN）

---

一、什么是人工神经网络？

人工神经网络（Artificial Neural Network，ANN）是一种模仿生物神经系统结构的计算模型，通过多层神经元的协同计算实现对复杂模式的学习。其核心是非线性变换与参数优化，使网络能拟合任意复杂函数。

生物神经元通过树突接收信号，在细胞体（soma）进行电化学整合，通过轴突传递至突触末梢；人工神经元则通过加权求和与激活函数处理输入，输出结果传递给下一层。这种结构使ANN在图像识别、自然语言处理等领域表现卓越。

---

二、神经元与神经网络的结构详解

2.1 人工神经元的结构

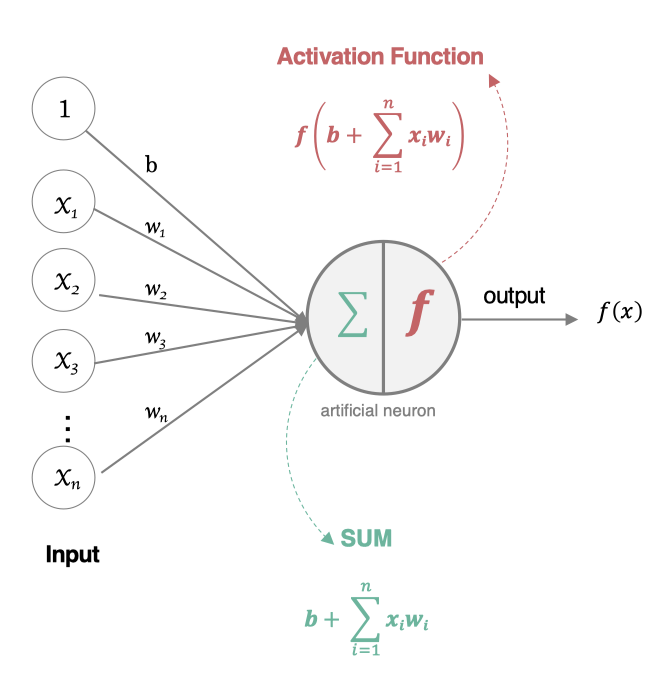
人工神经元是神经网络的基本单元，其结构模拟生物神经元的工作机制：

• 输入端：接收多个输入信号（$x_1,x_2,...,x_n$），对应生物神经元的树突。
• 权重与偏置：每个输入信号被赋予权重（$w_1,w_2,...,w_n$），表示该信号的重要性；偏置（$b$）用于调整神经元的激活阈值，类似生物神经元的静息电位。
• 整合单元：对输入信号进行加权求和，得到内部状态值（$z$）。
• 激活函数：对内部状态值进行非线性变换，输出激活值（$a$），模拟生物神经元的“激活-放电”过程。

结构示意图：

2.2 神经网络的层级结构

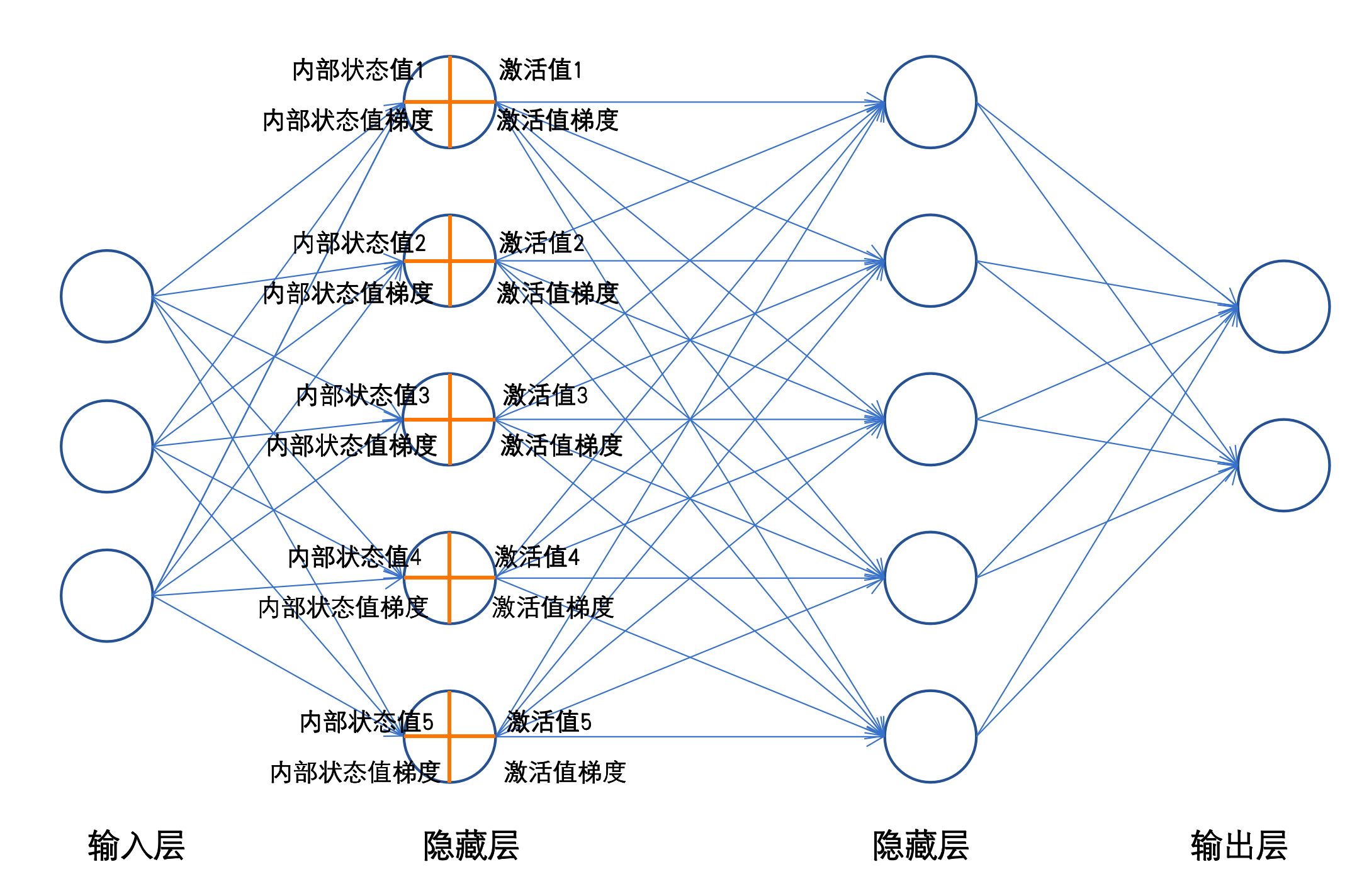
神经网络由多层神经元连接而成，典型结构包括：

1. 输入层：接收原始数据（如图像的像素值、文本的特征向量），神经元数量等于输入特征维度。
2. 隐藏层：位于输入层与输出层之间，负责特征提取与转换。隐藏层数量决定网络的“深度”，每层神经元数量可根据任务调整。
3. 输出层：输出预测结果，神经元数量由任务类型决定（如二分类问题用1个神经元，10分类问题用10个神经元）。

全连接神经网络（FCNN）的特点：

• 层内神经元无连接，层间神经元全连接（第$N$层每个神经元与第$N-1$层所有神经元相连）。
• 信息单向流动，属于前馈神经网络。

结构示意图：

---

三、单个神经元的计算过程

3.1 数学原理

单个神经元的计算分为两步：

1. 加权求和（内部状态值）
   对输入特征与权重的线性组合：
   $$z=\sum _{i=1}^n(w_i\cdot x_i)+b$$

2. 非线性变换（激活值）
   通过激活函数$f$处理内部状态值：
   $$a=f(z)$$

3.2 数值示例：单个神经元计算

假设神经元接收3个输入信号，具体参数如下：

• 输入特征：$x_1=1.2,x_2=3.4,x_3=2.6$
• 权重：$w_1=0.8,w_2=0.5,w_3=0.3$
• 偏置：$b=0.2$
• 激活函数：ReLU（$f(z)=\max (0,z)$）

步骤1：计算加权求和（$z$）
逐个计算每个输入与权重的乘积，再累加并加偏置：

• $w_1\cdot x_1=0.8\times 1.2=0.96$
• $w_2\cdot x_2=0.5\times 3.4=1.7$
• $w_3\cdot x_3=0.3\times 2.6=0.78$
• 求和：$0.96+1.7+0.78=3.44$
• 加偏置：$z=3.44+0.2=3.64$

步骤2：应用激活函数（$a$）
ReLU函数对$z=3.64$的处理：
$$a=\max (0,3.64)=3.64$$

输出结果：该神经元的激活值为$3.64$。

---

四、神经网络前向传播的计算过程

4.1 网络结构与参数

以一个含1个隐藏层的神经网络为例：

• 输入层：2个神经元（$x_1,x_2$）
• 隐藏层：2个神经元（$h_1,h_2$，激活函数为sigmoid）
• 输出层：1个神经元（$\hat{y}$，激活函数为sigmoid）

参数设置：

• 隐藏层权重矩阵：$W^{(1)}=\left[\begin{array}{cc}{w}_{11}^{(1)}& w_{12}^{(1)}\\ w_{21}^{(1)}& w_{22}^{(1)}\end{array}\right]=\left[\begin{array}{cc}0.3& 0.5\\ 0.2& 0.4\end{array}\right]$
• 隐藏层偏置：$b^{(1)}=\left[\begin{array}{c}{b}_1^{(1)}\\ b_2^{(1)}\end{array}\right]=\left[\begin{array}{c}0.1\\ 0.2\end{array}\right]$
• 输出层权重：$W^{(2)}=\left[\begin{array}{c}{w}_1^{(2)}\\ w_2^{(2)}\end{array}\right]=\left[\begin{array}{c}0.6\\ 0.7\end{array}\right]$
• 输出层偏置：$b^{(2)}=0.3$
• 输入：$x=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}1.0\\ 2.0\end{array}\right]$

4.2 隐藏层计算（$h_1,h_2$）

神经元$h_1$的计算：

1. 加权求和（$z_1^{(1)}$）：
   $$z_1^{(1)}=w_{11}^{(1)}{x}_1+w_{12}^{(1)}{x}_2+b_1^{(1)}$$
   代入数值：
   $$z_1^{(1)}=0.3\times 1.0+0.5\times 2.0+0.1=0.3+1.0+0.1=1.4$$

2. sigmoid激活（$a_1^{(1)}$）：
   $$a_1^{(1)}=\frac{1}{1+e^{-z_1^{(1)}}}=\frac{1}{1+e^{-1.4}}\approx \frac{1}{1+0.2466}\approx 0.8025$$

神经元$h_2$的计算：

1. 加权求和（$z_2^{(1)}$）：
   $$z_2^{(1)}=w_{21}^{(1)}{x}_1+w_{22}^{(1)}{x}_2+b_2^{(1)}$$
   代入数值：
   $$z_2^{(1)}=0.2\times 1.0+0.4\times 2.0+0.2=0.2+0.8+0.2=1.2$$

2. sigmoid激活（$a_2^{(1)}$）：
   $$a_2^{(1)}=\frac{1}{1+e^{-1.2}}\approx \frac{1}{1+0.3012}\approx 0.7685$$

4.3 输出层计算（$\hat{y}$）

1. 加权求和（$z^{(2)}$）：
   $$z^{(2)}=w_1^{(2)}{a}_1^{(1)}+w_2^{(2)}{a}_2^{(1)}+b^{(2)}$$
   代入数值：
   $$z^{(2)}=0.6\times 0.8025+0.7\times 0.7685+0.3\approx 0.4815+0.5380+0.3=1.3195$$

2. sigmoid激活（$\hat{y}$）：
   $$\hat{y}=\frac{1}{1+e^{-1.3195}}\approx \frac{1}{1+0.2665}\approx 0.7896$$

网络输出结果：$\hat{y}\approx 0.7896$

---

五、反向传播的详细计算过程

5.1 损失函数与梯度公式

设真实标签$y=1.0$，损失函数为均方误差（MSE）：
$$L=\frac{1}{2}(\hat{y}-y{)}^2$$

参数更新公式：
$$w=w-\eta \cdot \frac{\partial L}{\partial w}(\eta =0.1为学习率)$$

5.2 输出层梯度计算

1. 损失对输出层内部状态的梯度：
   $$\frac{\partial L}{\partial z^{(2)}}=(\hat{y}-y)\cdot \hat{y}\cdot (1-\hat{y})$$
   代入数值：
   $$\begin{array}{rl}\frac{\partial L}{\partial z^{(2)}}& =(0.7896-1.0)\times 0.7896\times (1-0.7896)\\ & =(-0.2104)\times 0.7896\times 0.2104\\ & \approx -0.0344\end{array}$$

2. 损失对输出层权重的梯度：

   • 对$w_1^{(2)}$：
     $$\frac{\partial L}{\partial w_1^{(2)}}=\frac{\partial L}{\partial z^{(2)}}\cdot a_1^{(1)}\approx -0.0344\times 0.8025\approx -0.0276$$
   • 对$w_2^{(2)}$：
     $$\frac{\partial L}{\partial w_2^{(2)}}=\frac{\partial L}{\partial z^{(2)}}\cdot a_2^{(1)}\approx -0.0344\times 0.7685\approx -0.0264$$

5.3 隐藏层梯度计算

1. 损失对隐藏层内部状态的梯度：

   • 对$z_1^{(1)}$：
     $$\begin{array}{rl}\frac{\partial L}{\partial z_1^{(1)}}& =\frac{\partial L}{\partial z^{(2)}}\cdot w_1^{(2)}\cdot {\sigma }^{\prime }(z_1^{(1)})\\ & \approx -0.0344\times 0.6\times 0.8025\times 0.1975\\ & \approx -0.0344\times 0.6\times 0.1585\\ & \approx -0.00325\end{array}$$
   • 对$z_2^{(1)}$：
     $$\begin{array}{rl}\frac{\partial L}{\partial z_2^{(1)}}& =\frac{\partial L}{\partial z^{(2)}}\cdot w_2^{(2)}\cdot {\sigma }^{\prime }(z_2^{(1)})\\ & \approx -0.0344\times 0.7\times 0.7685\times 0.2315\\ & \approx -0.0344\times 0.7\times 0.1779\\ & \approx -0.00430\end{array}$$

2. 损失对隐藏层权重的梯度：

   • 对$w_{11}^{(1)}$：
     $$\frac{\partial L}{\partial w_{11}^{(1)}}=\frac{\partial L}{\partial z_1^{(1)}}\cdot x_1\approx -0.00325\times 1.0=-0.00325$$
   • 对$w_{12}^{(1)}$：
     $$\frac{\partial L}{\partial w_{12}^{(1)}}=\frac{\partial L}{\partial z_1^{(1)}}\cdot x_2\approx -0.00325\times 2.0=-0.00650$$

5.4 参数更新

• $w_1^{(2)}$：
  $$w_1^{(2)}=0.6-0.1\times (-0.0276)\approx 0.6+0.00276\approx 0.6028$$
• $w_{11}^{(1)}$：
  $$w_{11}^{(1)}=0.3-0.1\times (-0.00325)\approx 0.3+0.000325\approx 0.3003$$

---

六、关键组件的数学解析

6.1 激活函数的导数特性

激活函数	公式	导数	特点
Sigmoid	$\sigma (x)=\frac{1}{1+e^{-x}}$	${\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))$	梯度范围(0,0.25)，易消失
Tanh	$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$	${\tanh }^{\prime }(x)=1-{\tanh }^2(x)$	梯度范围(0,1)，零中心化
ReLU	$\max =(0,x)$	$1$ if $x>0$ else $0$	缓解梯度消失，可能神经元死亡

6.2 参数初始化的数学依据

• Xavier初始化（适用于Sigmoid/Tanh）：
  确保输入输出方差一致：
  $$w\sim \mathcal{U}\left(-\sqrt{\frac{6}{fa{n}_{in}+fa{n}_{out}}},\sqrt{\frac{6}{fa{n}_{in}+fa{n}_{out}}}\right)$$

• Kaiming初始化（适用于ReLU）：
  考虑ReLU对梯度的影响：
  $$w\sim \mathcal{N}\left(0,\sqrt{\frac{2}{fa{n}_{in}}}\right)$$

6.3链式法则

链式法则的核心作用
神经网络的参数更新依赖反向传播算法，而反向传播的数学基础正是链式法则。其核心作用是：将复杂复合函数的求导分解为多个简单函数的导数乘积，从而高效计算损失函数对深层网络中每个参数的梯度。

具体来说，神经网络的前向传播是“输入→隐藏层→输出”的多层复合函数计算（例如 $y_{\text{pred}}=f_3(f_2(f_1(x)))$），损失函数 $L$ 是预测值 $y_{\text{pred}}$ 与真实值 $y_{\text{true}}$ 的函数（例如 $L=\text{Loss}(y_{\text{pred}},y_{\text{true}})$）。要计算损失对底层参数（如第一层权重 $w_1$）的梯度，需要通过链式法则逐层传递导数：
$$\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial y_{\text{pred}}}\cdot \frac{\partial y_{\text{pred}}}{\partial f_2}\cdot \frac{\partial f_2}{\partial f_1}\cdot \frac{\partial f_1}{\partial w_1}$$

没有链式法则，深层网络的参数梯度计算将变得极其复杂（需要直接对嵌套多层的函数求导），而链式法则通过“分步骤、传梯度”的方式，让反向传播高效可行。

形象例子：用“工厂流水线”理解链式法则
假设一个工厂的产品质量（类比损失 $L$）由三个环节的操作共同决定：

1. 原料处理（类比输入层 $x$）：工人A（类比权重 $w_1$）处理原料，产出半成品1；
2. 加工组装（类比隐藏层）：工人B（类比权重 $w_2$）用半成品1生产半成品2；
3. 质检包装（类比输出层）：工人C（类比权重 $w_3$）用半成品2生产最终产品。

如果最终产品质量不达标（损失 $L$ 大），管理者需要追溯每个工人的责任（计算 $\frac{\partial L}{\partial w_1},\frac{\partial L}{\partial w_2},\frac{\partial L}{\partial w_3}$）：

• 首先判断“质检包装”对质量的影响：产品质量差有多少比例是工人C的操作导致的（$\frac{\partial L}{\partial \text{半成品2}}$）；
• 再追溯“加工组装”：半成品2的缺陷有多少是工人B导致的（$\frac{\partial \text{半成品2}}{\partial \text{半成品1}}$）；
• 最后追溯“原料处理”：半成品1的缺陷有多少是工人A导致的（$\frac{\partial \text{半成品1}}{\partial w_1}$）。

链式法则的作用：将“总质量问题”分解为每个环节的责任比例，相乘后得到每个工人对最终质量的影响（例如 $\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial \text{半成品2}}\cdot \frac{\partial \text{半成品2}}{\partial \text{半成品1}}\cdot \frac{\partial \text{半成品1}}{\partial w_1}$）。

---

七、总结

单个神经元通过“加权求和+激活函数”实现非线性变换，是神经网络的基本计算单元；神经网络则通过多层神经元的嵌套计算，实现从输入到输出的特征转换（前向传播），并通过反向传播的梯度计算优化参数。

详细的数值计算过程展示了从输入信号到输出预测的完整逻辑，其中每一步加权求和、激活函数应用、梯度推导都严格遵循数学公式，是理解神经网络工作机制的核心。掌握这些细节，能帮助更深入地调试模型、优化网络结构，为复杂任务（如深度学习）奠定基础。