Bellman-Ford算法和Dijkstra算法都是求解图的最短路径的算法。Bellman是求单源点到各个顶点的最短路径，适用条件为有向或无向图，权重可为负值。当存在负权环路时，算法返回一个false值。该算法效率比较低，需要对边进行 |V|- 1 次松弛操作
Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E)。（V为给定图的顶点集合，E为给定图的边集合）
两者区别在于：Dijkstra要求图中不存在边权值之和为负数的环路，否则算法无法收敛；Bellman-Ford算法可以检测出图中是否存在权值之和为负数的环路。
Bellman-Ford算法功能：
给定一个加权连通图，选取一个顶点，称为起点，求取起点到其它所有顶点之间的最短距离，其显著特点是可以求取含负权边 图的单源最短路径。
Bellman-Ford算法思想：
- 1. 初始化所有点：每个点保存一个dist值，表示从源点到达这个点的最短距离，将原点的值设为0，其它的点的值设为无穷大 +∞（表示不可达），即： dist[v] ← +∞， dist[s] ←0 。
- 2. 迭代求解：进行循环，循环下标为从1到 n－1（n为图中节点的个数）。在循环内部，遍历所有的边，对边集E中的每条边进行松弛操作。使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离；（运行 |v|-1 次） 。
（松弛操作只需要进行 n-1 次。因为在一个含有n个顶点的图中，任意两点之间的最短路径最多包含n-1条边。
其实，n-1 次 只是一个上界（最大值），很多时候我们会在n-1轮之前就求出了最短路径。）
- 3. 检验负权回路：遍历途中所有的边（edge（u，v）），判断边集E中的每一条边的两个端点是否收敛。因为第2步中已经完成了 |v|-1 次 松弛操作，在第3步中，如果存在d（v）> d (u) + w(u,v)，则返回false，说明存在未收敛的顶点，也就是存在从源点可达的负权回路，这种情况下算法无解。否则返回true，算法可以运行处结果，并且从源点可达的顶点 v 的最短距离保存在 dist[v] 中。
（如果经过n-1次松弛操作后，仍然可以继续成功松弛，那么，此图必定存在负权回路。）
来看一个例子理解一下：
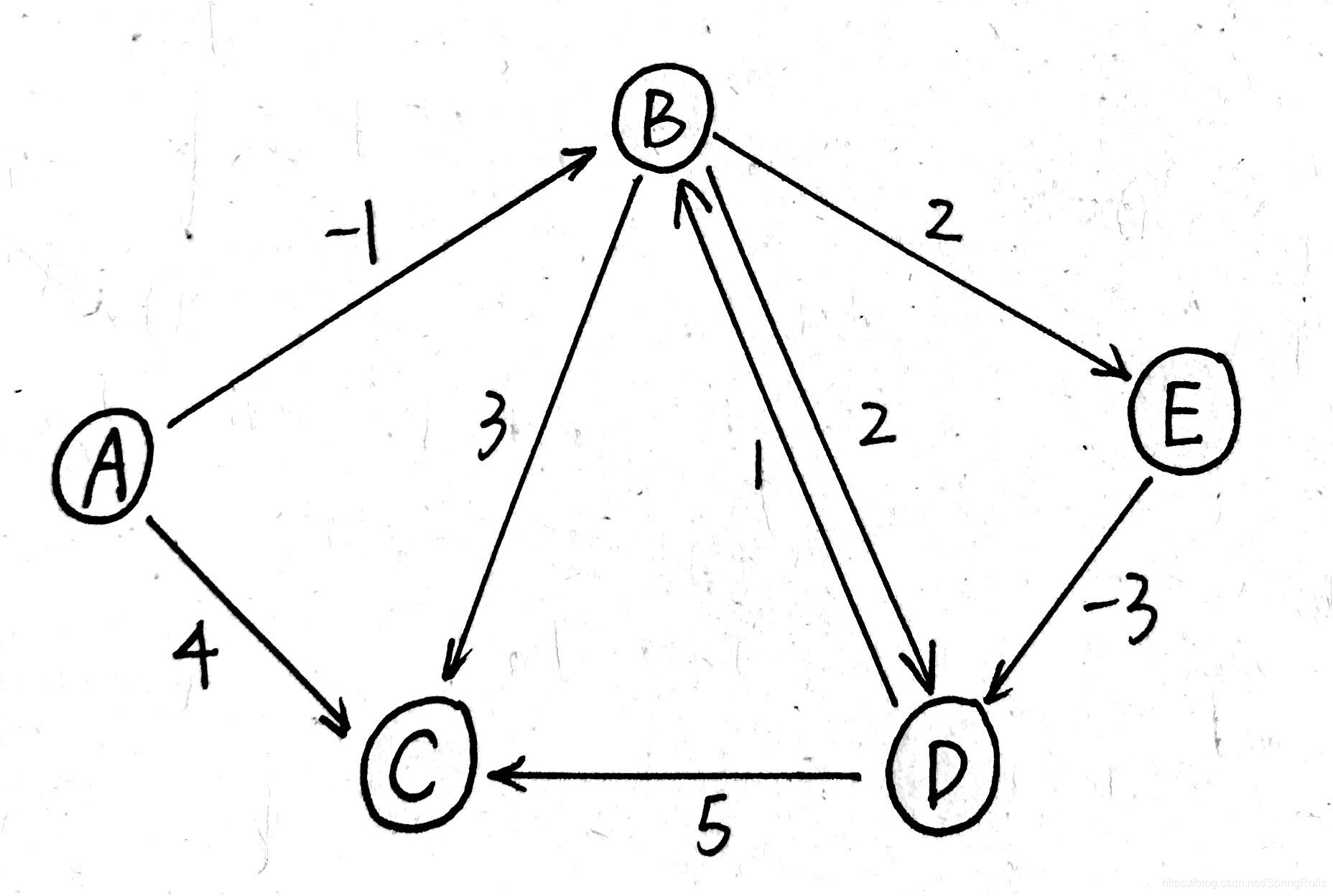
如下图所示，按 Bellman–Ford 算法思路 获取 起点A 到各节点的最短路径。由于该图顶点总数 n=5 个顶点，所以需要进行 5-1 = 4 次的遍历更新操作（即松弛操作），在每次松弛操作过程中，若能发现更短的路径则更新对应节点的 dist值。
1.首先初始化各节点，列出起点A到各个节点耗费的时间：
父节点 节点 初始化dist 执行线路 A A 0 - - B ∞ - - C ∞
- - D ∞ - - E ∞ -
2.进行第一次对所有边的松弛操作：
2.1 统计经过1条边所能到达的节点的值AB，AC：
AB:-1 AC:4
父节点 节点 dist
执行线路 A A 0 - A B -1 A->B A C 4
A->C - D ∞ - E ∞
2.2 统计经过2条边所能到达的节点的值BC,BD,BE：
BC:3 BE:2 BD:2
其中：以节点C为例，因为满足: dist(C) > dist(B) + weight(BC) ，即 4 > -1 + 3 ，所以C的dist更新为2
父节点 节点 dist 执行线路 A A 0 - A B -1 A->B B C 2
A->B->C B D 1 A->B->D B E 1 A->B->E
2.3 统计经过3条边所能到达的节点的值ED,DC：
ED:-3 DC:5 DB:1
父节点 节点 dist 执行线路 A A 0 - A B -1 A->B B C 2
A->B->C E D -2 A->B->E->D B E 1 A->B->E
3. 尝试再进行第2次遍历，对所有边进行松弛操作，发现没有节点需要进行更新，此时便可以提前结束遍历，优化效率
即：2.3中的表格就是最终结果，求出了源点A 到各个节点的最短路径与线路。
算法伪代码：
算法的核心代码：
//【核心代码】
for(int k=1; k<=n-1; k++)
{
for(int i=1; i<=m; i++)
{
// 松弛操作
// 这里也可以写为 dist[v[i]]=min(dist[v[i]],dist[u[i]]+w[i])
if(dist[v[i]] > dist[u[i]] + w[i])
{
dist[v[i]] = dist[u[i]] + w[i];
}
}
}
那么算法步骤第三步为何要判断是否存在负环路呢？存在负环路的情况为何无解呢？
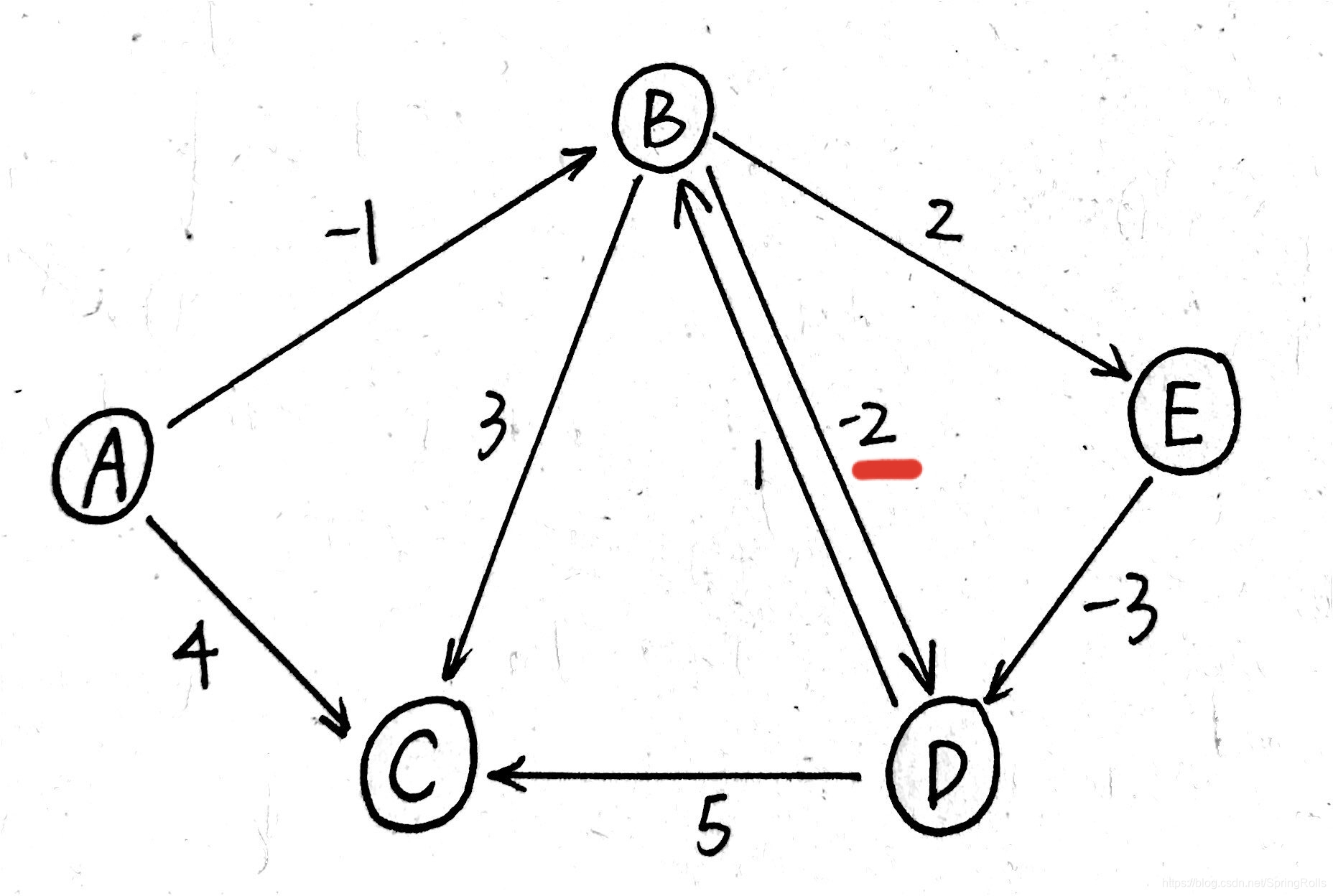
对刚刚例子中的图进行修改 将B->D 的2 改为 -2，这就使得B<->D这形成了负环路，所谓的负环路指的是环路权重之和为负数，比如下图中 1 + (-2) = -1 < 0即为负环路。
因为负环路可以无限执行循环步骤，试想，可以在 B->D->B->D...这边无限循环，所以B、D的取值可以无限小， 然后当B、D取值无限小后再从B、D节点出发到达其他各个节点，都会导致其它节点的取值同样接近无限小。所以，对于负环路的情况，Bellman–Ford 只能判断出图存在负环路，返回False，无法求出各个节点最短路径的意义。
以上的例子部分来自作者：CodeInfo 链接：https://juejin.im/post/5b77fec1e51d4538cf53be68
Java代码：
import java.util.Scanner;
public class BellmanFord {
public long[] dist; //dist数组 用于存放第0个顶点到其它顶点之间的最短距离
//-------内部类，表示图的一条加权边
class edge {
public int begin; //边的起点
public int end; //边的终点
public int weight; //边的权值
edge(int begin, int b, int value) { //带参构造
this.begin = begin;
this.end = end;
this.weight = weight;
}
}
//-------内部类结束
//返回第0个顶点到其它所有顶点之间的最短距离
public boolean getShortestPaths(int n, edge[] A) { //n是顶点总数, A是边集
dist = new long[n];
//第一步
for(int i = 1; i < n; i++) //i从1开始而不是从0开始，是因为源点不用初始化为无穷大
//初始化第0个顶点到其它顶点之间的距离为无穷大,即dist[i],此处用Integer型最大值表示
dist[i] = Integer.MAX_VALUE;
//第二步
for(int i = 1; i < n; i++) {
for(int j = 0; j < A.length; j++) {
//松弛操作
//意味着最短路径是先从s到a，再由a->b, 所以更新dist[b]的数据
if(dist[A[j].end] > dist[A[j].begin] + A[j].weight)
dist[A[j].end] = dist[A[j].begin] + A[j].weight;
}
}
//第三步
boolean judge = true; //judge为判断是否有负权环路的标志，默认不含有
for(int i = 1; i < n; i++) { //判断给定图中是否存在负环
if(dist[A[i].end] > dist[A[i].begin] + A[i].weight) { //如果仍然可以继续成功松弛
judge = false; //则存在负权环路，算法无法进行下去
break;
}
}
return judge;
}
public static void main(String[] args) {
BellmanFord test = new BellmanFord();
Scanner in = new Scanner(System.in);
System.out.println("请输入一个图的顶点总数n和边总数p：");
int n = in.nextInt();
int p = in.nextInt();
edge[] A = new edge[p];
System.out.println("请输入具体边的数据：");
for(int i = 0; i < p; i++) {
int a = in.nextInt();
int b = in.nextInt();
int w = in.nextInt();
A[i] = test.new edge(a, b, w);
}
if(test.getShortestPaths(n, A)) {
for(int i = 0; i < test.dist.length; i++)
System.out.print(test.dist[i]+" ");
} else
System.out.println("给定图中存在负环，没有最短距离");
}
}
结果：
另一种图解：（摘自啊哈算法）
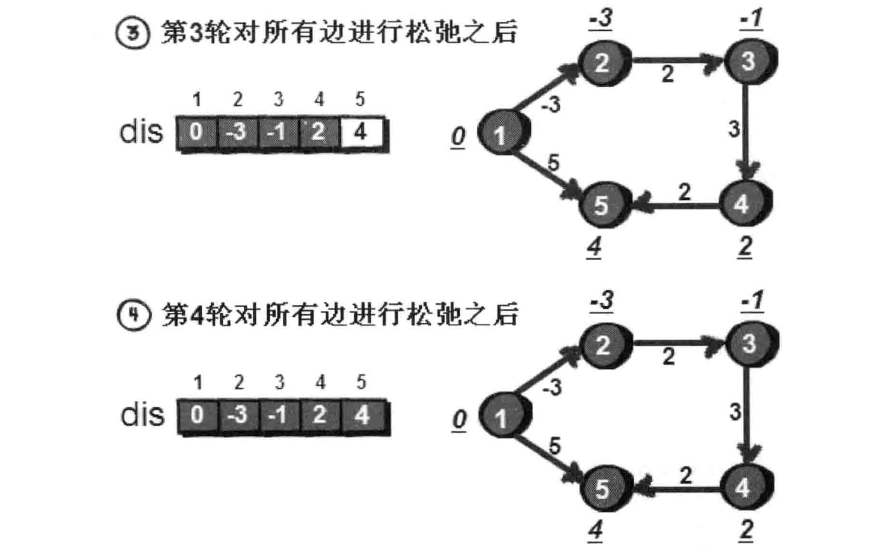
到达第4轮时，我们发现，其实第4轮的操作是多余的，因为dis数组的值没有发生任何变化。
扫一扫
404
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
