问题 H: Hunter’s Apprentice（由顶点判断多边形曲线边界的顺逆时针的情况）

题目描述

When you were five years old, you watched in horror as a spiked devil murdered your parents. You would have died too, except you were saved by Rose, a passing demon hunter. She ended up adopting you and training you as her apprentice.
Rose’s current quarry is a clock devil which has been wreaking havoc on the otherwise quiet and unassuming town of Innsmouth. It comes out each night to damage goods, deface signs, and kill anyone foolish enough to wander around too late. The clock devil has offed the last demon hunter after it; due to its time-warping powers, it is incredibly agile and fares well in straight-up fights.
The two of you have spent weeks searching through dusty tomes for a way to defeat this evil. Eventually, you stumbled upon a relevant passage. It detailed how a priest managed to ensnare a clock devil by constructing a trap from silver, lavender, pewter, and clockwork. The finished trap contained several pieces, which must be placed one-by-one in the shape of a particular polygon, in counter-clockwise order. The book stated that the counter-clockwise order was important to counter the clock devil’s ability to speed its own time up, and that a clockwise order would only serve to enhance its speed.
It was your responsibility to build and deploy the trap, while Rose prepared for the ensuing fight. You carefully reconstruct each piece as well as you can from the book. Unfortunately, things did not go as planned that night. Before you can finish preparing the trap, the clock devil finds the two of you. Rose tries to fight the devil, but is losing quickly. However, she is buying you the time to finish the trap. You quickly walk around them in the shape of the polygon, placing each piece in the correct position. You hurriedly activate the trap as Rose is knocked out. Just then, you remember the book’s warning. What should you do next?

输入

The first line of input contains a single integer T (1 ≤ T ≤ 100), the number of test cases. The first line of each test case contains a single integer n (3 ≤ n ≤ 20), the number of pieces in the trap. Each of the next n lines contains two integers xi and yi (|xi |, |yi | ≤ 100), denoting the x and y coordinates of where the ith piece was placed. It is guaranteed that the polygon is simple; edges only intersect at vertices, exactly two edges meet at each vertex, and all vertices are distinct.

输出

For each test case, output a single line containing either fight if the trap was made correctly or run if the trap was made incorrectly.

样例输入
复制样例数据 2
3
0 0
1 0
0 1
3
0 0
0 1
1 0

样例输出
fight
run

思路（ 转载）

1.遍历所有点，找到x最大的点Pm（该点一定在最右端曲线的“凸起”部分上），然后取该点前后各一个点Pm-1、Pm+1，组成向

量(Pm-1,Pm)、(Pm,Pm+1)。然后进行向量叉乘即可判断出顺时针或逆时针。

如图，规定向量叉乘使用“右手定则”

＋表示该点Pm和前后两个点组成的两个向量(Pm-1,Pm)、(Pm,Pm+1),叉乘得到的向量指向z轴负方向；

－表示(Pm-1,Pm)x(Pm,Pm+1)得到的向量指向z轴方向。

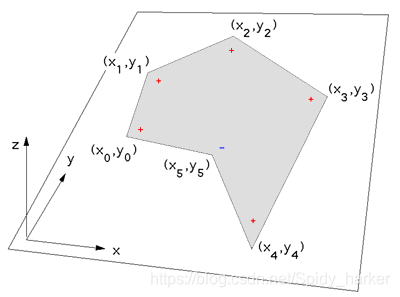
NOTE：这里必须进行遍历寻找凸点，否则若多边形含有凹的部分，并且选取的点于凹部分中，会得到相反的结果。

#include <iostream>

using namespace std;

int main()
{
    int T;cin>>T;
    while(T--)
    {
        int n;cin>>n;
        int sign;
        int maxn=-101;
        int x[n+5],y[n+5];
        for(int i=0;i<n;i++)
        {
            cin>>x[i]>>y[i];
            if(maxn<x[i])
            {
                sign=i;
                maxn=x[i];
            }
        }
        if(sign!=n-1)
        {
        	int x1=x[sign]-x[sign-1],y1=y[sign]-y[sign-1];
        	int x2=x[sign+1]-x[sign],y2=y[sign+1]-y[sign];
        	if(x1*y2>y1*x2) cout<<"fight"<<endl;
        	else cout<<"run"<<endl;
        }
        else///要特判最大的x为最后一个点的情况，那么他的下一个点就是（x0，y0）
        {
        	int x1=x[sign]-x[sign-1],y1=y[sign]-y[sign-1];
        	int x2=x[0]-x[sign],y2=y[0]-y[sign];
        	if(x1*y2>y1*x2) cout<<"fight"<<endl;
        	else cout<<"run"<<endl;
        }
    }
}

2.Green公式

double d = 0;
for (int i = 0; i < n - 1; i++) {
    d += -0.5 * ( y[i + 1] + y[i]) * (x[i + 1] - x[i]);
}
if ( d > 0)
    cout << "fight" << endl;
else
    cout << "run" << endl;