HDU 5017 Ellipsoid（模拟退火）_ellipsoid correct-优快云博客

本文介绍了一种计算椭球面上任一点到原点最短距离的方法，并提供了一个使用C++实现的具体算法示例。该算法通过迭代逼近的方式找到满足精度要求的最短距离。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Ellipsoid

Problem Description

Given a 3-dimension ellipsoid(椭球面)

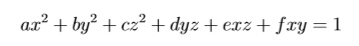
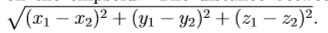
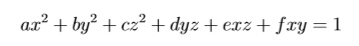
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x₁,y₁,z₁) and (x₂,y₂,z₂) is defined as

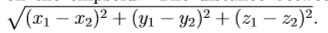
Input

There are multiple test cases. Please process till EOF.

For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f(0 ≤ d,e,f < 1), as described above. It is guaranteed that the input data forms a ellipsoid. All numbers are fit in double.

Output

For each test contains one line. Describes the minimal distance. Answer will be considered as correct if their absolute error is less than 10^-5.

Sample Input

1 0.04 0.01 0 0 0

Sample Output

1.0000000

【思路分析】
求椭球面上的点到原点的最短距离。网上很多说是模拟退火，个人感觉此题局部最优解就是全局最优解，即结果是一个单峰函数，顶多算个爬山算法。

代码如下：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
#define r 0.99
#define inf 1e8
#define eps 1e-8
double a,b,c,d,e,f;
int direction[10][2];

void init()
{
    int x = 0;
    for(int i = -1;i <= 1;i++)
    {
        for(int j = -1;j <= 1;j++)
        {
            direction[x][0] = i;
            direction[x][1] = j;
            x++;
        }
    }
}
double distances(double x,double y,double z)
{
    return sqrt(x * x + y * y + z * z);
}
double caculateZ(double x,double y)//根据求二次方程原理求z
{
    double A = c;
    double B = d * y + e * x;
    double C = a * x * x + b * y * y + f * x * y - 1.0;
    double delta = B * B - 4.0 * A * C;

    if(delta < 0.0)
        return inf;
    else
    {
        double z1 = (-B + sqrt(delta)) / (2.0 * A);
        double z2 = (-B - sqrt(delta)) / (2.0 * A);
        if(distances(x,y,z1) < distances(x,y,z2))
            return z1;
        else
            return z2;

    }
}

int main()
{
    init();
    while(scanf("%lf %lf %lf %lf %lf %lf",&a,&b,&c,&d,&e,&f) != EOF)
    {
        double x = 0,y = 0,z = sqrt(1.0 / c);
        double step = 1.0;
        while(step > eps)
        {
            for(int i = 0;i < 9;i++)
            {
                double x1 = x + step * direction[i][0];
                double y1 = y + step * direction[i][1];
                double z1 = caculateZ(x1,y1);
                if(z1 >= inf)
                    continue;
                if(distances(x1,y1,z1) < distances(x,y,z))
                {
                    x = x1;
                    y = y1;
                    z = z1;
                }
            }
            step *= r;
        }
        printf("%.7lf\n",distances(x,y,z));
    }
    return 0;
}