LeetCode 221. Maximal Square

Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.

For example, given the following matrix:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 4.

题意：给出一个由0、1填充的二维矩阵，找出只包含1的最大的正方形，并返回它的面积。

举一个栗子，现在我们要找下面这个矩阵在matrix[2][3]和matrix[2][4]的面积：
1 0 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
我们发现：划线的点处的最大面积为红、黄、绿三个正方形最小边+1的平方

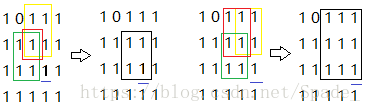
下面我们看代码如何实现，代码中我会说明思路并举一个样例栗子：

class Solution {
public:
    /*
    假设dp[i][j]代表i行j列square的最大边长，我们发现：
    (1) dp[0][i] = matrix[0][i] (0 <= i < matrix[0].size)
        dp[j][0] = matrix[j][0] (0 <= j < matrix.size)
    (2) if matrix[i][j] != 0 :
       dp[i][j] = minNum(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1;

    比如：

    1) matrix:          2) matrix:          3) matrix:          5) matrix:          
    1 0 1 0 0           [1 0] 1 0 0         1 [0 1] 0 0         1 0 1 [0 0]
    1 0 1 1 1           [1 0] 1 1 1         1 [0 1] 1 1         1 0 1 [1 1]
    1 1 1 1 1           1 1 1 1 1           1 1 1 1 1           1 1 1 1 1
    1 0 0 1 0           1 0 0 1 0           1 0 0 1 0     ...   1 0 0 1 0     ...

    1) dp[][]           2) dp[1][1]         3) dp[1][2]         5) dp[1][4]
    1 0 1 0 1           1 0 1 0 1           1 0 1 0 1           1 0 1 0 1
    1 * * * *           1 0 * * *           1 0 1 * *           1 0 1 1 1    
    1 * * * *           1 * * * *           1 * * * *           1 * * * * 
    1 * * * *           1 * * * *           1 * * * *     ...   1 * * * *     ...

    7) dp[2][1]         8) dp[2][2]         9) dp[2][3]         10) dp[2][4]
    1 0 1 0 1           1 0 1 0 1           1 0 1 0 1           1 0 1 0 1
    1 0 1 1 1           1 0 1 1 1           1 0 1 * *           1 0 1 1 1    
    1 1 * * *           1 1 1 2 2           1 1 1 2 2           1 1 1 2 2 
    1 * * * *           1 * * * *           1 * * * *     ...   1 * * * *     ...    

    */
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty()) return 0;

        int rows = matrix.size(), cols = matrix[0].size();
        int res = matrix[0][0] - '0';
        vector<vector<int> > dp(rows, vector<int>(cols, 0)); // 每个点的最大边长

        for(int i = 0; i < cols; ++i){  // 初始化第一行
            dp[0][i] = matrix[0][i] - '0';
            res = max(dp[0][i], res);   // 记录最大的边长
        }

        for(int i = 0; i < rows; ++i){  // 初始化第一列
            dp[i][0] = matrix[i][0] - '0';
            res = max(dp[i][0], res);   // 记录最大的边长
        }

        for(int i = 1; i < rows; ++i)
            for(int j = 1; j < cols; ++j)
                if(matrix[i][j] != '0'){
                    // 取决于三个正方形中最小正方形的边长 + 1
                    dp[i][j] = minNum(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1;
                    res = max(dp[i][j] , res);  // 记录最大的边长
                }

        return res * res;   // 返回边长的平方
    }

private:
    // 返回三个数中最小的数
    int minNum(const int &a, const int &b, const int& c){
        return a < b? (a < c ? a : c) : (b < c ? b : c);
    }
};

分析时间复杂度和空间复杂度：
Time Complexity：O(n*m) (m、n 分別代表行列数)
Space Complexity：O(n*m)

优化 Space Complexity：
我们发现，其实每次我们计算dp[i][j]都只依赖于dp[i - 1][j]、dp[i][j - 1]、dp[i - 1][j - 1]，所以对于dp[][]，我们实际上只需要维持一行就可以了。不清楚的可以看上面代码举的栗子，计算第2行的dp[2][]时，我们只用到了第一行的dp[1][]。（当然也可以维持一列，其实还有一种方法不需要额外空间，但是需要修改matrix的值）

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty()) return 0;

        int rows = matrix.size(), cols = matrix[0].size();
        int res = 0; // 最大边长
        vector<int> dp(cols, 0);

        for(int i = 0; i < cols; ++i){
            dp[i] = matrix[0][i] - '0';
            res = max(dp[i], res);  // 第0行是否存在最大边长
        }

        for(int i = 1; i < rows; ++i){
            int leftUp = dp[0];
            dp[0] = matrix[i][0] - '0';
            res = max(dp[0], res);    // 第0列是否存在最大边长
            for(int j = 1; j < cols; ++j){
                int temp = dp[j];   // 相当于记录dp[i - 1][j - 1]
                if(matrix[i][j] != '0'){
                    dp[j] = minNum(dp[j - 1]/*dp[i][j - 1]*/, dp[j] /*d[i - 1][j]*/, leftUp/*dp[i - 1][j - 1]*/) + 1;
                    res = max(dp[j], res);
                }
                else
                    dp[j] = 0; // 因为漏了matrix[i][j] == 0的时候，dp[j] = 0， 调了好久
                leftUp = temp;   // dp[i - 1][j - 1]
            }
        }
        return res * res;// 返回边长的平方
    }
private:
    // 返回三个数中最小的数
    int minNum(const int &a, const int &b, const int& c){
        return a < b? (a < c ? a : c) : (b < c ? b : c);
    }
};

到这里已经把Space Complexity控制在了O(n)或者O(m)