逻辑回归（Logistic Regression）

基础不牢，地动山摇。

文中加粗的字母（如，等）默认为列向量。

用机器学习算法做分类任务的小伙伴一定使用过“逻辑回归分类器”这个东西，顾名思义，既然是个分类器，那逻辑回归肯定是用在分类任务中的。我在上一篇博客中介绍过回归任务与分类任务的区别：回归任务用来预测一个数值，分类任务用来预测一个标签。逻辑回归既然是用在分类任务中的，那它的名字里为什么要有“回归”两个字呢？

我们可以来大胆地假设一下，逻辑回归是不是在用回归的思想做分类。

1. 如何用回归的思想做分类

让我们以最简单的二分类任务为例，假设样本的真实分类标签只能是或者。而线性回归模型产生的预测值是实值，它的取值范围可以是一切实数。于是，我们想办法将回归模型产生的实值转换为分类任务所需的或者，这样也就实现了回归任务和分类任务的相互转化。

最简单的方法是将实值输入单位阶跃函数：

若预测值大于零就判标签为，小于零就判标签为，预测值为临界值可以任意判别，示意图如下：

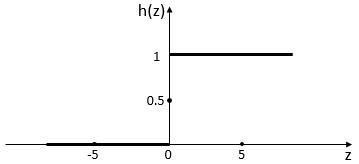
2. Logistic函数

自此，我们已经用一个单位阶跃函数将回归模型的思想与分类任务结合起来了。但是，单位阶跃函数并不连续，这会给我们带来一些不便，于是我们希望找到能在一定程度上近似单位阶跃函数的“替代函数”，Logistic函数正是这样一个常用的替代函数：

它的函数图像如下：

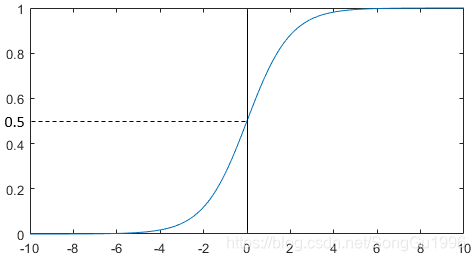
从图中可以看出，Logistic函数是一种“Sigmoid函数”。它能将回归模型输出的值转化成一个到之间的值，与单位阶跃函数不同，这个值不再是最终的预测结果，而是可以理解为：样本标签为的概率。得到所有样本的值之后，我们可以使用一个阈值将其分成两部分，小于阈值的判断为标签，大于阈值的判断为标签，这样就达到了分类的效果。

李航《统计学习方法》上的描述为：表示样本标签为的概率，则表示样本标签为的概率，将与比大小，将样本分到概率值较大的那一类，这种思想其实就类似于将阈值设为0.5。

使用Logistic函数来代替单位阶跃函数有以下几个好处：

① Logistic函数连续、充分光滑、单调递增，能最大程度地保留自身的特点；
② Logistic函数不是直接预测出类别，而是可以得到近似的概率预测，这对许多需要利用概率辅助决策的任务很有用；
③ Logistic函数是任意阶可导的凸函数，有很好的数学性质。

3. 二分类的逻辑回归

经过上面的描述，大家应该已经清楚了如何用回归的思想来做分类任务。下面我们来定义一下逻辑回归的目标：

为线性模型找到一组最合适的和，使得在全部样本上预测正确的概率最大。

如何才能找到这样的参数呢，请接着往下看。

将线性模型产生的预测值：，代入到Logistic函数：

可以得到：

把这个式子稍微转化一下，可以得到：

上面说过，我们可以把,也就是看成样本标签为的概率，则可以看成样本标签为的概率，则我们可以把上式用概率的形式改写一下：

其中，读作：在给定输入下，样本标签为的概率；读作：在给定输入下，样本标签为的概率。

将上式拆开写，可以得到二分类逻辑回归的模型：

从上面的描述可以看出，服从伯努利分布，伯努利分布的一些介绍如下图：

为了便于表达，记，，则单个样本的概率质量函数可以记为：

假设现在给定训练集，则全部样本上预测正确的概率，即似然函数为：

我们用极大似然估计法来估计和，根据上式写出对数似然函数：

为了便于讨论，令：

，

则可以简写为：，

上面的对数似然函数可以简写为：

所以二分类的逻辑回归的目标就是：找出能使这个对数似然函数取最大值的参数。

由于我们习惯于让一个函数越小越好，所以我们把最大化转化为最小化。此外，使用一个正的常数系数来缩放对数似然函数，并不会改变参数估计的结果，所以我们把最大化转化为最小化，式子如下：

其中，是样本数，在吴恩达的机器学习视频课程中，使用上式作为逻辑回归的损失函数，我们可以用梯度下降法对进行参数估计，用梯度更新参数的步骤如下：

其中，为学习率。更新参数是一个耗时耗力的过程，我们可以交给计算机去完成。

假设我们使用极大似然估计得到的参数为：，那么最终学到的二分类的逻辑回归模型为：

4. 多分类的逻辑回归

假设样本的真实标签值的取值集合为：，那么多分类的逻辑回归模型可以表达为：

二分类逻辑回归的参数估计方法也可以推广到多分类的情况，这里不再单独说明。 

参考：

李航《统计学习方法》
周志华《机器学习》
逻辑回归(logistics regression)-优快云博客
【机器学习】【逻辑回归】最大似然估计的推导和求解步骤和梯度上升算法求解_推导最大似然损失函数的梯度-优快云博客