机器学习算法系列（九）-多分类对数几率回归算法（Multinomial Logistic Regression）

阅读本文需要的背景知识点：对数几率回归算法、一丢丢编程知识

一、引言

  前面介绍了对数几率回归算法，该算法叫做回归算法，但其实是用来处理分类问题，将数据集分为了两类，用 0、1 或者是 -1、1 来表示。现实中不仅仅有二分类问题，同时也有很多是例如识别手写数字 0～9 等这种多分类的问题，下面我们就来介绍下多分类的对数几率回归算法¹（Multinomial Logistic Regression Algorithm）

二、模型介绍

  多分类可以通过对二分类进行推广来得到，通过一些策略，可以用二分类器来解决多分类的问题。常用的策略有：一对一（One vs. One / OvO）、一对其他（One vs. Rest / OvR）、多对多（Many vs. Many / MvM）
  例如有如下数据集分类：

一对一（One vs. One/OvO）
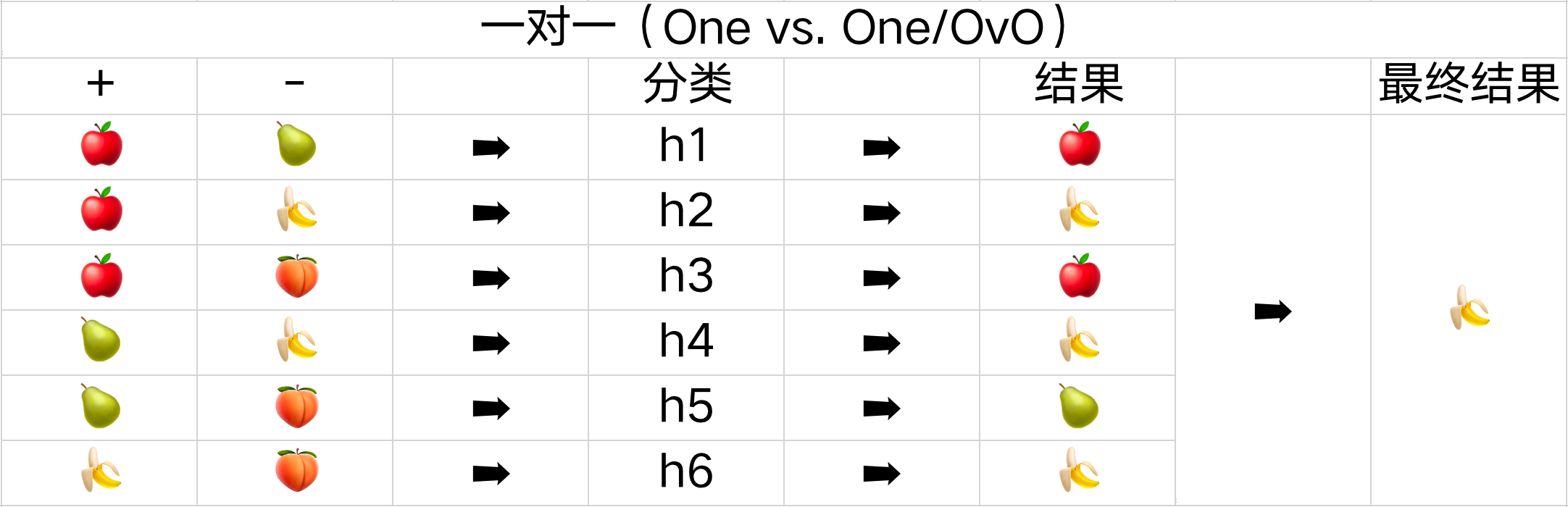
  一对一的策略是每次只处理两个类别，将全部 N 个类别两两配对，会产生 $\frac{N(N-1)}{2}$ 个二分类的任务。
  如下面的表格所示，一共有苹果、梨子、香蕉、桃子这四种分类，会产生六种不同的结果，所以需要六个不同的分类器。需要预测新的是哪一类时，只需通过这些分类器的结果，其中预测最多的分类就是最终的分类结果。

一对其他（One vs. Rest/OvR）
  一对其他的策略是将一个类别作为正例，其余所有的类别当成反例，全部 N 个类别会产生 N 个二分类的任务。
  如下面的表格所示，一共有苹果、梨子、香蕉、桃子这四种分类，会产生四种不同的结果，所以需要四个不同的分类器。需要预测新的是哪一类时，只需选择分类器预测结果为正的结果作为最终分类结果，若有多个分类器都预测为正，则选择权重最大的分类器的分类结果。

多对多（Many vs. Many/MvM）
  多对多的策略是将若干类别作为正例、若干类别作为反例，通过一定的编码，实现多分类的问题。常见的主要有二元码与三元码。二元码将每种类型看成正例或者反例，三元码除了正反例以外有一个停用类，即分类时不使用。
  二元码：如下面的表格所示，一共有苹果、梨子、香蕉、桃子这四种分类，这里用了五个分类器来编码结果，如 h1 将苹果、香蕉、桃子作为反例，将梨子作为正例。需要预测新的是哪一类时，通过五个分类器的结果与原始结果比较，这里使用海明距离，即结果有多少不一致的数量，距离最小的分类就是最终分类结果。

  三元码：如下面的表格所示，一共有苹果、梨子、香蕉、桃子这四种分类，这里用了七个分类器来编码结果，如 h2 将苹果作为反例，将香蕉、桃子作为正例，不使用梨子的分类。需要预测新的是哪一类时，通过这七个分类器的结果与原始结果比较，一样使用海明距离，距离最小的分类就是最终分类结果。

  可以看到 OvO、OvR 是 MvM 的特殊情况。OvO 相对 OvR 来说，需要更多的分类器模型，所以其存储与预测阶段的开销会更大，但在训练阶段使用的数据量更小，相对来说这部分开销会小一些。MvM 这种编码的方式具备一定的纠错能力，某个分类器的结果错误，可能对最后的分类结果不会有影响，所以这种方式叫做纠错输出码（Error Correcting Output Codes / ECOC）

多分类对数几率回归
  多分类对数几率回归与二分类的对数几率回归不同的是，不再使用逻辑函数（Logistic Function），而是使用Softmax函数²（Softmax Function），该函数可以看作是对逻辑函数的一种推广。
  Softmax 函数能将一个含任意实数的 K 维向量 z “压缩”到另一个 K 维实向量 σ(z) 中，使得每一个元素的范围都在(0,1)之间，并且所有元素的和为1。
$$\sigma (z{)}_j=\frac{e^{z_j}}{{\sum }_{i=1}^K{e}^{z_i}}(j=1,\cdots ,K)$$

  假设有 K 种分类，可以将每种分类的条件概率写成 Softmax 函数的形式，即将每个分类的线性组合结果带入到 Softmax 函数中：
$$P(y=j\mid x,W)=\frac{e^{W_j^{T}x}}{{\sum }_{i=1}^K{e}^{W_i^{T}x}}(j=1,\cdots ,K)$$

  其假设函数为：
$$h(x)=\left[\begin{array}{c}P(y=1\mid x,W)\\ P(y=2\mid x,W)\\ \cdots \\ P(y=K\mid x,W)\end{array}\right]=\frac{1}{{\sum }_{i=1}^K{e}^{W_i^{T}x}}\left[\begin{array}{c}{e}^{W_1^{T}x}\\ e^{W_2^{T}x}\\ \cdots \\ e^{W_K^{T}x}\end{array}\right]$$

  由于多分类对数几率回归使用了 Softmax 函数，所以该回归算法有时也被称为 Softmax 回归（Softmax Regression）

多分类对数几率回归的代价函数
  与二分类对数几率回归的代价函数一样，也是使用最大似然函数的对数形式，首先写出其似然函数：
$$L(W)=\prod _{i=1}^N\prod _{j=1}^K{\left(\frac{e^{W{j}^T{X}_i}}{{\sum }_{k=1}^K{e}^{W_k^T{X}_i}}\right)}^{1_j\left(y_i\right)}$$

  其中指数部分为指示函数（indicator function），代表当第 i 个 y 的值等于分类j时函数返回 1，不等于时返回 0，如下所示：
$$1_A(x)=\{\begin{array}{cc}1& x\in A\\ 0& x\notin A\end{array}$$

  然后对似然函数取对数后加个负号，就是多分类对数几率回归的代价函数了，我们的目标依然是最小化该代价函数：
$$\mathrm{Cost}(W)=-\sum _{i=1}^N\sum _{j=1}^K{1}_j\left(y_i\right)\ln ({\sum }_{k=1}^{}$$