高数Umaru系列（9）——哈士奇

高数Umaru系列（9）——哈士奇

SDUT OJ 高数Umaru系列（9）——哈士奇

Problem Description
由于高数巨养的喵星人太傲娇了，要天天吃新鲜猫粮而且还经常欺负高数巨，所以高数巨决定买几条哈士奇尝尝鲜。这天高数巨来到了二手狗市场买哈士奇，高数巨看完了所有的哈士奇，记下了每条哈士奇的价格，并根据对它们的好感程度给它们每只都赋予了一个萌值。高数现在手里有X元，她想通过购买若干条哈士奇来获得尽可能多的萌值。现在给定高数巨手里的钱X以及N条哈士奇的价格和萌值，求高数巨最多可获得多少萌值

Input
多组输入。

对于每组输入，第一行有两个整数N，X（1 < = N < = 100，1 < = X < = 1000），分别表示哈士奇的数量和高数巨的钱数

接下来的N行每行有两个整数Pi，Mi（1 < = Pi,Mi < = 100），分别表示第i条哈士奇的价格和萌值

Output
对于每组数据，输出一个整数，表示高数巨最多可以获得的萌值，每组输出占一行

Sample Input
2 100
50 20
60 40
3 100
20 55
20 35
90 95
1 10
20 50
Sample Output
40
95
0
Hint

Source
Shannon

该问题是典型的01背包问题；
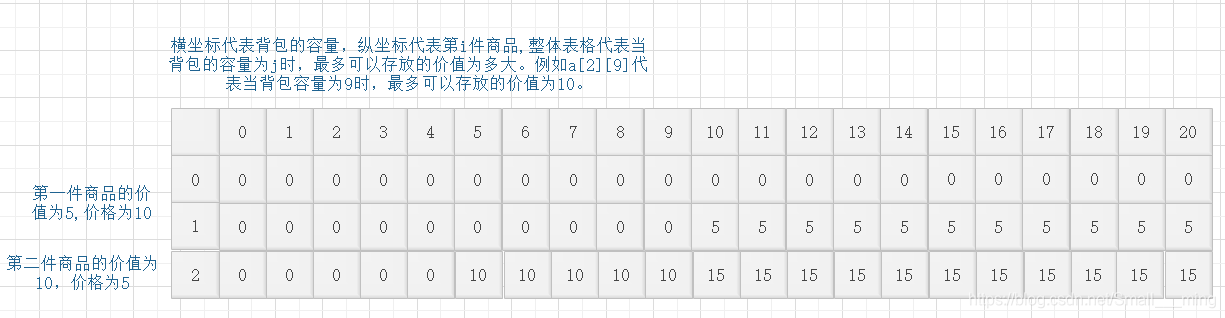
对于01背包问题的理解，可以这么理解，一个小偷去商店里偷东西，他的背包容量是一定的，但是他想偷在他的背包容量下所能偷的最大价值！所以对于第i件商品，小偷要选择偷还是不偷，如果偷的话当前背包的容量就要减掉相应的空间，同时加上相应的价值。如果不偷，那么空间不减，价值也不变。所以可以得出状态转换方程：
背包容量够偷第i件商品 f(i,j) = max{f(i-1,j-p[i])+m[i],f(i-1，j)}
背包容量不够偷第i件商品 f(i,j) = f(i-1,j)
其中 f(i,j)代表此时背包的价值。i代表已经偷了i-1件商品，现在要做决定偷不偷第i件，j代表当前的空间。如果背包容量够的话就要看偷了第i件商品与不偷第i件商品的区别，偷的话，背包的空间减小p[i]大小，变为j-p[i]，背包的价值变为
f(i-1,j-p[i])+m[i]。不偷的话背包的空间不变，还是为j，价值也不便还是为当前背包的价值f(i-1,j)。看哪一个价值更好一些，如果。如果背包容量不够只能选择不偷，则背包的价值也就跟偷了i-1件商品的价值一致，背包的空间即为方程中的j也不会变化。如果这段文字理解了，那么问题也就解决了，就是求f(i,j)对应的二维数组。具体代码如下。

#include<bits/stdc++.h>
using namespace std;
#define N 110
#define M 1110
#define inf 0x3f3f3f3f
int main()
{
    int n, x;
    while(cin >> n >> x)
    {
        //注意！
        //本题是多组输入，所以一定要在这里初始化
        int p[N] = {0}, m[N] = {0};
        //v[N][M]代表所求的数组
        int v[N][M] = {0};
        for(int i = 1; i <= n; i++)
            cin >> p[i] >> m[i];
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= x; j++)
            {
                if(j >= p[i])//能装下的情况
                {
                    //在这里一定是v[i-1][***]
                    //i代表前面i件的最大性价比
                    //这里要求前i件
                    //只知道前i-1件商品的最大性价比，所以只可以用v[i-1][***]
                    int t1 = v[i-1][j-p[i]] + m[i];
                    int t2 = v[i-1][j];
                    v[i][j] = max(t1,t2);
                }
                else//装不下的情况
                    v[i][j] = v[i-1][j];
            }
        }
        cout << v[n][x] << endl;
    }
    return 0;
}