二分查找算法详细汇总

二分查找算法详细汇总

二分查找算法介绍模板

二分查找算法也称折半查找算法，是在有序数组中用到的较为频繁的一种查找算法。在未接触二分查找算法时，最通用的一种做法是，对数组进行遍历，跟每个元素进行比较，即顺序查找。二分查找较顺序查找更优，因为这种算法每一次比较都使查找范围缩小一半。

算法思想

二分查找算法是建立在有序数组基础上的。算法思想为：

1. 查找过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则查找过程结束；
2. 如果某一待查找元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟第1点一样从中间元素开始继续进行查找。
3. 如果在某一步骤数组为空，则代表找不到。

举例说明

模板实现

（1）递归方式实现

主函数：
public static void main(String[] args) {
    int[] nums = {1,2,7,9,14,25,95,100};//定义需要查找的数组
    int left = 0;
    int right = arr.length - 1;
    int index = binarySearchByRecurion(nums, left,right,9);
    if (index != -1) {
        System.out.println("在数组中找到该值,index= " + index);
    }else {
        System.out.println("在数组中未找到该值...");
    }
}
二分查找【递归方式实现】
private static int binarySeach(int[] nums, int left, int right, int target) {
    if (left <= right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            return mid;
        }else if(nums[mid] > target) {
            return binarySeach(nums,left,mid - 1,target);
        }else {
            return binarySeach(nums,mid + 1,right,target);
        }
    }
    //如果未找到，返回-1
    return -1;
}

（2）非递归方式实现

主函数
public static void main(String[] args) {
    int[] nums = {1,2,7,9,14,25,9,100};//定义需要查找的数组
    int index = binarySearchByNoRecurion(nums, 9);
    if (index != -1) {
        System.out.println("在数组中找到该值,index= " + index);
    }else {
        System.out.println("在数组中未找到该值...");
    }
}
二分查找函数【非递归方式实现】
private static int binarySeach(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            return mid;
        }else if (nums[mid] > target) {
            right = mid - 1;
        }else {
            left = mid + 1;
        }
    }
    return -1;
}

二分查找问题相关难点问题1[前缀和 + 二分查找 + 带你飞跃这三题]

LeetCode1011. 在 D 天内送达包裹的能力[中等题]

问题描述:

传送带上的包裹必须在 D 天内从一个港口运送到另一个港口。

传送带上的第 i 个包裹的重量为 weights[i]。每一天，我们都会按给出重量的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。

返回能在 D 天内将传送带上的所有包裹送达的船的最低运载能力。

示例 1：

输入：weights = [1,2,3,4,5,6,7,8,9,10], D = 5
输出：15
解释：
船舶最低载重 15 就能够在 5 天内送达所有包裹，如下所示：
第 1 天：1, 2, 3, 4, 5
第 2 天：6, 7
第 3 天：8
第 4 天：9
第 5 天：10

请注意，货物必须按照给定的顺序装运，因此使用载重能力为 14 的船舶并将包装分成 (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) 是不允许的。 

示例 2：

输入：weights = [3,2,2,4,1,4], D = 3
输出：6
解释：
船舶最低载重 6 就能够在 3 天内送达所有包裹，如下所示：
第 1 天：3, 2
第 2 天：2, 4
第 3 天：1, 4

示例 3：

输入：weights = [1,2,3,1,1], D = 4
输出：3
解释：
第 1 天：1
第 2 天：2
第 3 天：3
第 4 天：1, 1

提示：

1. 1 <= D <= weights.length <= 50000
2. 1 <= weights[i] <= 500

题解1:

第一种方法 : 使用暴力法进行求解,即能够满足最小运载能力的重量必须大于等于所有物品重量的最大值才可以,故我们选择先锁定weights数组的最大值,以该值作为基准的起始值,进行判断,如果其能够保证在D天完成运载,则输出该值,否则,我们将其增大,直到找到满足的第一个值即可…

代码:

class Solution {
    public int shipWithinDays(int[] weights, int D) {
        //记录当前weights最高的重量
        int maxWeight = 0;
        int n = weights.length;
        for (int i = 0; i < n; i++) {
            if (weights[i] > maxWeight) {
                maxWeight = weights[i];
            }
        }
        while (true) {
            int target = maxWeight;
            int days = 0;
            int weight = 0;
            int p = 0;
            while (p < n) {
                //增加当天的载重
                weight += weights[p];
                //如果总的重量小于当前最低运载能力
                if (weight < target) {
                    p++;
                }else {
                    //此时存在总的重量 = 当前最低运载能力 或者 > 当前最低运载能力
                    //如果刚好等于当前运载能力,我们需要将p指针右移一位
                    if (weight == target) {
                        p++;
                    }
                    //无论等于还是大于,所需天数加1,总的重量归零
                    days++;
                    weight = 0;
                }
            }
            //如果退出while循环,weight不为0,表示最后还没有比较完,我们继续将days加1
            if (weight != 0) days++;
            //此时如果花费的天数小于所需的天数,则我们可以在当前最低运载能力为target的情况下,完成D天内的运载
            if (days <= D) return target;
            //否则我们将minWeight继续加1,进行下一轮的比较
            maxWeight++;
        }
    }
}

但是上面的方法时间复杂度为O(n^2),我们下面选择时间复杂度为O(nlogn)的二分查找算法

题解2:

首先此题我们先来得到以下定论:

我们如果在运载能力为x的情况下,可以在D天内运送完所有的包裹,则我们的运载能力凡是大于x,则也一定能够在D天内运送完所有的包裹

故:

肯定存在一个运载能力的下限值target,使得当运载能力x >= target时,我们可以在D天内运送完所有的包裹;当x < target时,我们无法在D天内运送完所有的包裹,这里的target即为我们需要查找的目标值

我们使用二分查找的方法寻找target的值,那么如何判断给定运载能力x,就可以在D天内运送玩所有的包裹??

使用贪心算法进行求解:

由于我们的weights数组的包裹按照顺序进行运送,因此我们从数组的weights的首元素开始进行遍历,将连续的包裹都安排在同一天进行运送.则当这批包裹的重量大于运载能力x时,我们就需要将最后一个包裹取出来,安排到新的一天,然后继续向下遍历,这里的思路和上面我们的思路是一致的.当我们遍历完整个数组的时候,就得到了最少需要运送的天数了.

最后我们将最少运送的天数和需要的天数D进行比较:

当其小于等于D,说明我们当前的运载能力能够满足D天运送结束,我们就选择忽略二分的右半部分区间,再左半区间继续寻找更小的值

当其大于D,说明我们当前的运载能力不能满足D天运送结束,我们就选择忽略二分的左半部分区间(都不满足情况…)

二分查找的左右边界: 即为运载能力的左右边界

左边界 : 我们不能拆分一个包裹,因此运载能力不能小于所有包裹中最重的那一个,故左边边界为weights中元素的最大值

右边界: 运载能力也不会大于所有的包裹的重量之和,即右边界为weights中元素之和

代码:

public int shipWithinDays03(int[] weights, int D) {
    //左边界初始值为最大值
    int left = Arrays.stream(weights).max().getAsInt();
    //右边界初始值为weights数组元素之和
    int right = Arrays.stream(weights).sum();
    while (left < right) {
        //获取中间值
        int mid = (left + right) / 2;
        //定义运送的天数
        int days = 1;
        //记录当前天的运送包裹重量之和
        int sum = 0;
        for (int weight : weights) {
            if (weight + sum > mid) {
                //说明加上当天的重量超过了运载能力
                ++days;
                sum = 0;
            }
            sum += weight;
        }
        //最后判断天数
        if (days <= D) {
            //说明当前运载能力 >= 最佳的运载能力,我们的target值可以在[left,mid]中继续优化
            //[这里注意: 因为mid同样满足我们的条件，故我们将right = mid，而不是mid + 1]
            right = mid;
        }else {
            //说明当前运载能力小了
            left = mid + 1;
        }
    }

    //最后的left值即为所需的最小运载能力
    return left;
}

LeetCode875. 爱吃香蕉的珂珂[中等]

问题描述:

珂珂喜欢吃香蕉。这里有 N 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。

珂珂可以决定她吃香蕉的速度 K （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 K 根。如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）。

示例 1：

输入: piles = [3,6,7,11], H = 8
输出: 4

示例 2：

输入: piles = [30,11,23,4,20], H = 5
输出: 30

示例 3：

输入: piles = [30,11,23,4,20], H = 6
输出: 23

提示：

• 1 <= piles.length <= 10^4
• piles.length <= H <= 10^9
• 1 <= piles[i] <= 10^9

题解:

可以看出这题的类型和上面的思路很相似…

public int minEatingSpeed(int[] piles, int h) {
    //首先定义珂珂吃香蕉的速度: 由于 1 <= piles[i] <= 10^9
    int left = 1;
    int right = 1000000000;
    while (left < right) {
        int mid = (left + right) / 2;
        //当前吃的速度为mid的条件下,所需要的小时(time),初始化为0
        int times = 0;
        for (int pile : piles) {
            int time = (int) Math.ceil((double) pile / (double) mid);
            times += time;
        }
        if (times <= h) {
            right = mid;
        }else {
            left = mid + 1;
        }
    }
    return left;
}

LeetCode410. 分割数组的最大值[困难]

问题描述:

给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。

设计一个算法使得这 m 个子数组各自和的最大值最小。

示例 1：

输入：nums = [7,2,5,10,8], m = 2
输出：18
解释：
一共有四种方法将 nums 分割为 2 个子数组。 其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

示例 2：

输入：nums = [1,2,3,4,5], m = 2
输出：9

示例 3：

输入：nums = [1,4,4], m = 3
输出：4

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 106
• 1 <= m <= min(50, nums.length)

题解:

public int splitArray(int[] nums, int m) {
    //首先获各自和的最大值的左右边界
    int left = Arrays.stream(nums).max().getAsInt();
    int right = Arrays.stream(nums).sum();

    while(left < right) {
        int mid = (left + right) / 2;
        int cnt = 1;
        int sum = 0;
        for (int num : nums) {
            if (sum + num > mid) {
                ++cnt;
                sum = 0;
            }
            sum += num;
        }
        //比较此时mid作为各自和的最大值，所分割的数组的个数
        if (cnt <= m) {
            //此时还可以在[left,mid]中继续寻找更小的最大值
            right = mid;
        }else {
            //此时数组的个数超过了m，需要在[mid + 1,right]中继续寻找
            left = mid + 1;
        }
    }
    return left;
}

新式二分查找问题

我们从剑指的第11题入手: 剑指 Offer 11. 旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。

示例 1：

输入：[3,4,5,1,2]
输出：1

示例 2：

输入：[2,2,2,0,1]
输出：0

新式二分法介绍 ;

我们说二分法求解问题,首先必须保证数组是排序的,即有序的,但是有的时候以及排好序的数组发生了旋转,此时我们仍然可以使用二分法来求解问题,只是此时二分法的代码需要发生一些变化,即我们所说的新式二分法,即通过旋转数组以及题目的要求寻找二分的规律.

我们来看这一题: 说一个递增的排序数组中输出其最小元素,此时我们通过画图(如下所示),来寻找其中的规律:

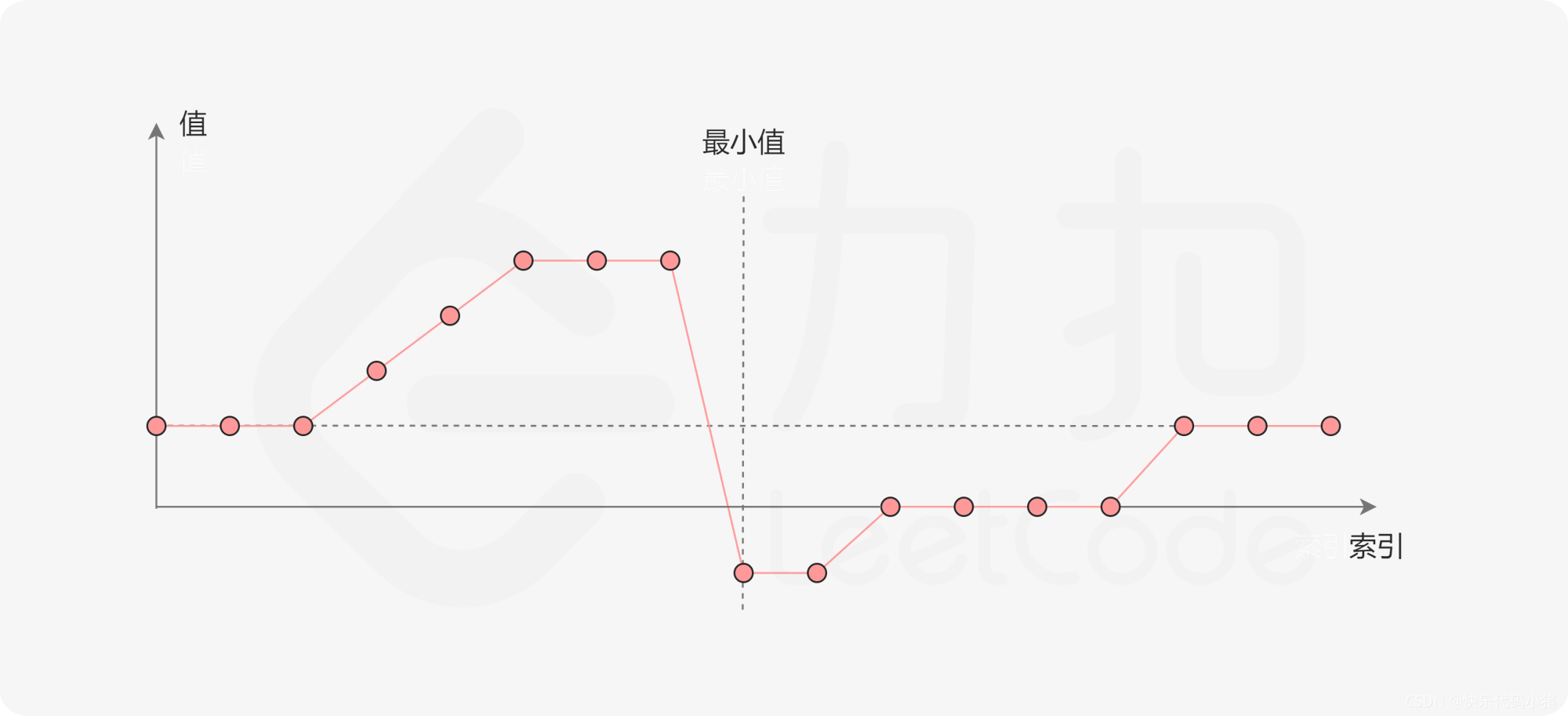
☆☆☆☆☆可以看出对于数组的最后一个元素(我们设其为x) :

在最小值右侧的元素,他们的值一定小于等于x

在最小值左侧的元素,他们的值一定大于等于x

通过上述规律,新式二分法的思路如下所示:

在二分查找的每一步中,左边界为left,右边界为right,区间的中点pivot = (left + right) / 2,向下取整

此时我们将nums[pivot] 与右边界 nums[right]进行比较,可能会出现以下三种情况:

第一种情况 : nums[pivot] < nums[right],说明nums[pivot]是最小值右侧的元素(也有可能就是nums[pivot]),即我们的最小值位于pivot 的左侧

第二种情况 : nums[pivot] > nums[right],说明nums[pivot]是最小值左侧的元素,即我们的最小值位于pivot的右侧

第三种情况 : nums[pivot] == nums[right],这是由于存在重复元素导致的,我们并不能确定nums[pivot]究竟是在最小值的左侧还是右侧,此时我们选择使用O(n)的缩进法,将right索引左移一位

当二分查找结束,此时nums[left],即left索引对应的值即为该旋转数组的最小元素的值

class Solution {
    public int minArray(int[] nums) {
        //使用新式二分法进行计算
        int left = 0;
        int right = nums.length - 1;
        while(left < right) {
            int pivot = (left + right) / 2;
            if(nums[pivot] < nums[right]) {
                //说明最小值位于pivot的左侧
                right = pivot;
            }else if(nums[pivot] > nums[right]) {
                //说明最小值位于pivot的右侧
                left = pivot + 1;
            }else {
                //此时无法确定最小值的位置,我们选择right指针左移一位
                right--;
            }
        }
        //while循环结束,我们返回left索引的值
        return nums[left];
    }
}

此时我们可以根据这种新式二分法的方法,解决LeetCode的第33题,第88题,第153题,以及第154题,其中第154题和上面的剑指的第11题相同,下面就不再列出了…

LeetCode 153. 寻找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

提示：

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• nums 中的所有整数 互不相同
• nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

题解:

此题和上面的例题唯一的区别,就在于此时num的元素互不相同,也就不存在我们所说的第三种情况

class Solution {
    public int findMin(int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        while(left < right) {
            int pivot = (left + right) >> 1;
            if(nums[pivot] < nums[right]) {
                //说明最小值在pivot的左侧
                right = pivot;
            }else {
               //说明最小值在pivot的右侧
                left = pivot + 1;
            }
        }
        return nums[left];
    }
}

新式二分法变形问题

LeetCode33. 搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

• 1 <= nums.length <= 5000
• -10^4 <= nums[i] <= 10^4
• nums 中的每个值都 独一无二
• 题目数据保证 nums 在预先未知的某个下标上进行了旋转
• -10^4 <= target <= 10^4

**进阶：**你可以设计一个时间复杂度为 O(log n) 的解决方案吗？

题解:

这道题和上面不同的地方在于不是寻找最小值,而是寻找目标数,故我们此时我们使用新式二分法,需要比较的不是中间索引和right索引的值的大小关系,而是比较中间索引的值和寻找目标数的大小关系:

数组进行旋转以后:

我们按照二分法的算法思路:首先定义左指针left和右指针right,分别指向数组的索引为0的位置和数组末尾(n - 1)的位置;

此时我们获取中间索引 mid = (left + right) >> 1;

我们首先判断当前nums[mid] 是否等于 target的值 ? 如果相等,直接返回mid

否则我们进行二分法搜索,这里由于数组不是单调递增的,故我们二分法需要进行调整

此时如下图所示 , 我们此时获取的中间索引将旋转数组切分为[left , mid - 1]以及[mid + 1 , right]两部分:

存在的情况分为以下三种情况:

(1)第一种情况 : mid索引刚好将数组分成两个有序的数组

(2)第二种情况 : mid索引将数组分为[left,mid - 1]为两个有序的,[mid + 1,right]为一个有序的

(3)第三种情况 : mid索引将数组分为[left,mid - 1]为一个有序的,[mid + 1,right]为两个有序的

如下图所示:

故我们首先需要判断nums[left] 和nums[mid]的值的大小关系 :

(1)如果nums[left] <= nums[mid] : 说明此时[left,mid]是单调递增的!

我们则选择进一步判断:

​ (1)如果nums[left] <= target < nums[mid] : 则表示target在[left,mid - 1]之间,将right = mid – 1

​ (2)否则表示target > nums[mid] : 则将left = mid + 1

(1)如果nums[left] > nums[mid] : 说明此时[mid + 1,right]是单调递增的!

我们也需要进一步判断:

(1)如果此时nums[mid] < target <= nums[right] : 则表示target在[mid + 1,right]之间,将left = mid + 1

​ (2)否则表示target < nums[mid] : 则将right = mid – 1

最后如果仍未找到,则返回-1

注意 : 这道题的nums数组的所有元素都是独一无二,不重复的!!!

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;  //获取数组的长度
        if(n == 0) return -1;
        int left = 0;
        int right = n - 1;
        while(left <= right) {
            //获取中间索引
            int mid = (left + right) >> 1;
            if(nums[mid] == target) return mid;
            //比较left索引位置的值和mid索引位置的值
            if(nums[left] <= nums[mid]) {//说明[left,mid]是递增的,这里等号需要,例如[3,1],获取left和mid索引相同
                if(nums[left] <= target && target < nums[mid]) {
                    right = mid - 1;
                }else {
                    //说明target > nums[mid]
                    left = mid + 1;
                }
            }else { //说明[mid + 1,right]是递增的
                if(nums[mid] < target && target <= nums[right]) {
                    left = mid + 1;
                }else {
                    //说明target < nums[mid]
                    right = mid - 1;
                }
            }
        }
        //如果仍未找到target的值
        return -1;
    }
}

LeetCode81. 搜索旋转排序数组 II

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true

示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

提示：

• 1 <= nums.length <= 5000
• -104 <= nums[i] <= 104
• 题目数据保证 nums 在预先未知的某个下标上进行了旋转
• -104 <= target <= 104

进阶：

• 这是 搜索旋转排序数组 的延伸题目，本题中的 nums 可能包含重复元素。
• 这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

题解:

这道题和上面的那道题唯一的区别就在于,元素的值可能是重复的,那么我们对于出现重复的值的时候,就无法使用二分判断,mid的左侧还是右侧是有序的了,比如:nums = [1,0,1,1,1],我们查找target = 0

第一次mid = 2,此时你会发现,nums[left] == nums[mid],而此时我们无法知晓[left,mid],[mid + 1,right]哪个是只有一个递增序列的,故我们需要剔除掉这种重复元素的情况

其实处理也很简单:

我们在每一次获取到mid的索引值以后,如果当前nums[mid] != target时,我们在进行上述判断之前,加一层筛选:

如果 nums[left] == nums[mid] left++

如果nums[right] == nums[mid] right—

这样使得最后进行上述判断时避免例子中的情况发生!

class Solution {
    public boolean search(int[] nums, int target) {
        int n = nums.length;  //获取数组的长度
        if(n == 0) return false;
        int left = 0;
        int right = n - 1;
        while(left <= right) {
        	int mid = (left + right) >> 1;
            if(nums[mid] == target) return true;
            if(nums[left] == nums[mid]) {
                ++left;
            }else if(nums[mid] == nums[right]) {
                --right;
            }else if(nums[left] < nums[mid]) {//说明[left,mid]是递增的,这里无需等号,因为等号的情况上面已经单独讨论了
                if(nums[left] <= target && target < nums[mid]) {
                    right = mid - 1;
                }else {
                    left = mid + 1;
                }
            }else { //说明[mid + 1,right]是递增的
                if(nums[mid] < target && target <= nums[right]) {
                    left = mid + 1;
                }else {
                    right = mid - 1;
                }
            }
        }
        return false;
    }
}

注意 : 上面的第153题使用这种新式二分法变形(比较nums[left] 和 nums[mid]的值也可以求的最小值)

class Solution {
   public int findMin(int[] nums) {
        int min = 5000;
        int left = 0;
        int right = nums.length - 1;
        while(left <= right) {
            int mid = (left + right) >> 1;
            if(nums[left] <= nums[mid]) { //[left,mid]是单调递增的
                if(nums[left] < min) {
                    min = nums[left];
                }
                left = mid + 1;
            }else {//[mid + 1,right]是单调递增的
                if(nums[mid] < min) {
                    min = nums[mid];
                }
                right = mid - 1;
            }
        }
        return min;
    }
}