聚类 之 DBSCAN

前面介绍的 KMeans 和 MeanShift 算法对于球状类的数据，聚类效果较好。对于非球状数据，如环状，就无能为力了。这次，给大家介绍一个同KMeans一样十分简单的基于密度的聚类方法：DBSCAN 聚类

DBSCAN 聚类基本原理

DBSCAN 聚类的核心思想是：从某个核心点出发，不断向密度可达的区域扩张，从而得到一个包含核心点和边界点的最大化区域，区域中任意两点密度相连。

DBSCAN 聚类流程简述

相比 K-Means 聚类，DBSCAN 原理同样简单，但不需要人为指定分成几类。

DBSCAN 聚类算法的大致思想就是 “能者居之，和气生财” ：

1. 首先，对每个点，以半径为 $R$（超参1） 圈定其势力范围。

2. 这一届的大佬们很霸气哈，不依靠小弟们的投票产生了。本着能者居之的原则，势力范围内有足够的点就可以毛遂自荐当大佬了。

   统计每个点势力范围内包含数据的个数。如果个数大于等于 $ϵ$（超参1），则该点为大佬，即核心点；若个数数量小于 $ϵ$，则

3. 对于能力不够的点，就要选择投靠大佬了。

   查看该点是否在某个大佬的势力范围内。若在，则为该大佬的小弟，即边界点；否则为孤魂野鬼，即噪声点（连投靠山头的机会都没有，太惨了o(╥﹏╥)o）。

4. 能者居之的制度导致部分大佬的势力范围重叠了。一山容不下二虎，势力范围重叠的大佬们产生了冲突。本着和气生财的原则，相互之间距离小于 $R$ 的大佬们自发合并山头，相互抱团。

• 注意：上面涉及的两个超参是需要用户人为指定的哈。
  
  

实例演示

还是老套路哈，举一个非常形象简单的例子。

如下图所示，有6个点，从图上看应该可以分成两堆，前三个点一堆，后三个点另一堆。现在我手工地把MeanShift 算法的计算过程演示一下，同时检验是不是和预期一致：

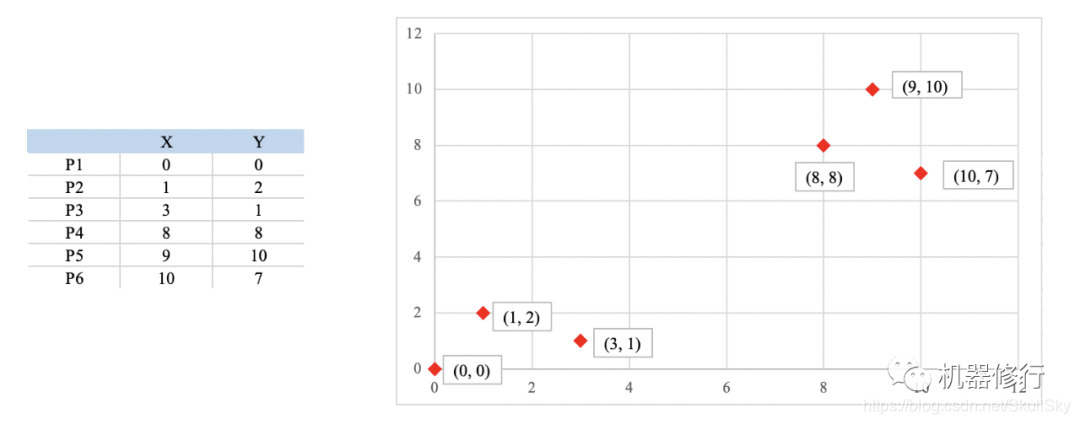
1. 以 $R=3$ 为半径，圈定每个点的势力范围。
2. 开始毛遂自荐当大佬：
   令 ϵ = 2 \epsilon=2 ϵ=<