力扣54、螺旋矩阵的一点想法(Python)

最新推荐文章于 2025-07-29 19:45:28 发布

原创最新推荐文章于 2025-07-29 19:45:28 发布 · 863 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #矩阵 #算法

由于从刷题开始到现在一共没有一年多，差不多从50题往后才开始能独立完成一部分代码，本次开始将分享一些做题的idea，不需要多少高深的知识，从零开始，共同努力！

54.螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

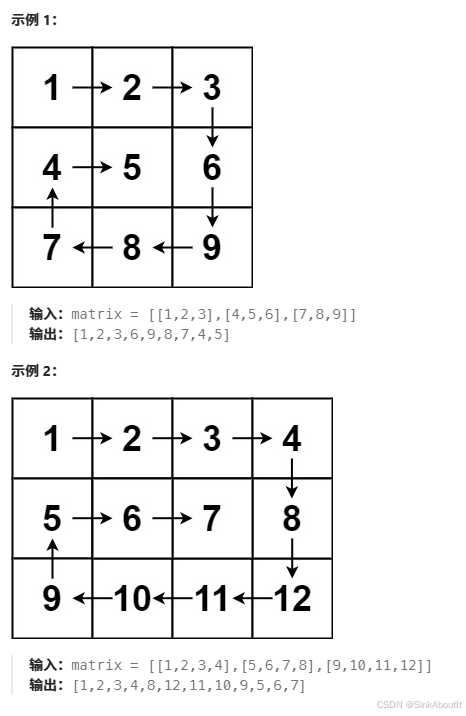（图片来源于leetcode）

可以观察到，本身按序排列的二维矩阵，根据顺时针的方式螺旋至矩阵的中心，难点一在于我们进行遍历矩阵时，应该用什么逻辑进行遍历，难点二在于如果我们想更改这个矩阵，应该如何转换矩阵的形式。

由于本题没有硬性要求我们在原矩阵进行操作，因此我们可以引申出两种思路，一种为在原矩阵基础上进行遍历，另一个是改变矩阵的形式进行输出。

一、遍历矩阵

首先，我们可以观察到，在给出的示例，遍历的顺序时是从第一行第一个元素开始从左向右，然后到达列的最大值时，向下进行遍历，可知这时的遍历顺序从行不动，列向右运动到列不动，行向下运动。直至行向下运动到达底部后，转而回归到行不动列动，只不过遍历是顺序改为反向，我们可以用range(r,l-1,-1)的方式实现反向操作，其中r为右边界，l为左边界。到达左边界后再向上运动，后向右运动，但这里注意，再一次向右运动相当于进入了下一个循环，也就是说我们从开始的向右运动到下一次向右运动，要经过4次转向周期。

由于我们每次到达边界后，下一次将不会到达当前边界，而是类似向内收缩一格，由此我们可以进行定义边界变量，为l (left) ,r (right) ,t (top) ,b (botton) ，分别对应着左边界，有边界，上边界，下边界。

当我们向右运动时，到达右边界后，说明第一行已遍历完毕，我们可以将上边界下移一格，同理，当我们向下运动，到达下边界后，说明右侧的一列已遍历完毕，我们可以将右边界左移一格。我们停止所有操作的条件为l>r或者t>b。由此可得以下代码

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix: return []
        l,r,t,b,res = 0, len(matrix[0]) - 1,0,len(matrix) - 1,[]
        while True:
            for i in range(l, r + 1):res.append(matrix[t][i])
            t +=1
            if t>b : break
            for i in range(t,b + 1): res.append(matrix[i][r])
            r -= 1
            if l > r: break
            for i in range(r,l-1,-1):res.append(matrix[b][i])
            b -= 1
            if t>b :break
            for i in range(b,t-1,-1):res.append(matrix[i][l])
            l += 1
            if l > r:break
        return res

为了防止矩阵为空，我们设置限制条件为如果矩阵为空，则返回空列表。我们将左边界，上边界赋值为0，将右边界和下边界分别赋值为列的长度-1与行的长度-1。最终结果保存至res。

二、旋转矩阵后输出

我们可以注意到，每次进行遍历的元素都集中在外侧，而遍历完一次后当前行或列将不再被使用，因此我们可以想到，如果每次遍历完当前行或列，我们可以把当前行或列把其从原矩阵中剔除掉，为了方便起见，我们都是直接剔除掉第一行，由此我们需要进行90°旋转的操作。

这里我们引用第48题、旋转图像作为前置知识。

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

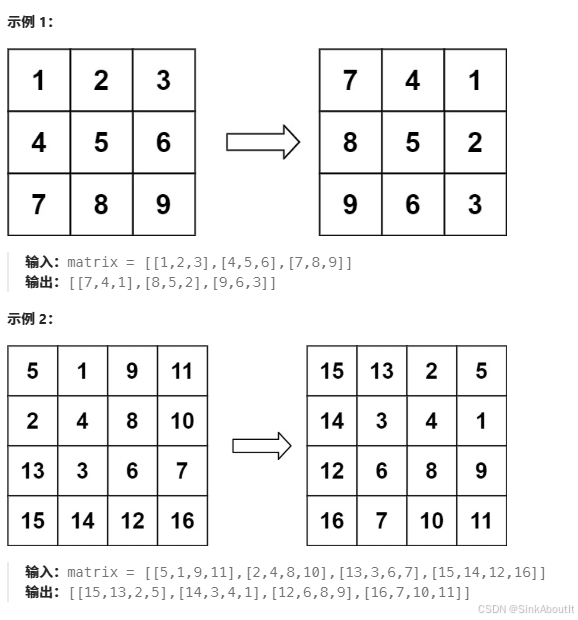（图片来源于leetcode）

在我们进行90°旋转时，我们可以有两种思路，

一、找规律

我们可以直接观察数字而不是图像，我们直接看输入 [[ 1, 2, 3],[ 4, 5, 6],[ 7, 8, 9]]

而输出变为了 [[ 7, 4, 1],[ 8, 5, 2],[ 9, 6, 3]]， 我们可以由此总结规律：从后往前，二维列表中，其中的每一个子列表，如果序数为0，将被放置进序数为0的矩阵，而且是从后往前遍历的顺序，例如[ 1, 2, 3],1的序数为0，因此放在序数为零的列表中，即[7,4,1]中，由此我们可以进行代码实现：

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        new_matrix = []
        n = len(matrix)
        for i in range(n):
            row = []
            for j in range(n):
                row.append(matrix[n-j-1][i])
            new_matrix.append(row)
        for i in range(n):
            matrix[i] = new_matrix[i]

这里的 i 为行， j 为列，n 为子列表的个数，在每一行中，我们每次初始化row，然后进入第二层for-loop循环，row.append(matrix[n - j - 1][i]) 这里将i 相放置列的位置，相当于我们将i固定住，也就是我们需要抽取的每一个子列表的序数号，而[n - j - 1]则是为了方便我们从后向前进行抽取列表，把得到的数据保存在row中并放置在新创建的new_matrix当中。

二、转置＋翻转

在我们进行对矩阵的转置后，再进行左右翻转，将得到90°旋转后的图像

1	2	3
4	5	6
7	8	9

1	4	7
2	5	8
3	6	9

7	4	1
8	5	2
9	6	3

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        matrix = list(map(list,zip(*matrix)))
        res = [row[::-1] for row in matrix]
        return res

转置矩阵我们将使用 matrix = list(map(list,zip(*matrix)))

假设matrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]

首先 *matrix 是一个解包操作，将矩阵的每一行作为独立的参数传递给 zip 函数。
zip 函数会将这些行重新组合，使得每一列变成一个新的元组，解包后传递给 zip 的参数是 (1, 2, 3), (4, 5, 6), (7, 8, 9)。zip 会将它们组合为：[(1, 4, 7), (2, 5, 8), (3, 6, 9)]，map(list, ...) 将每个元组转换为列表，最终结果为：[[1, 4, 7], [2, 5, 8], [3, 6, 9]]

因此我们的matrix = list(map(list,zip(*matrix)))能够直接将将矩阵进行转置，

res = [row[::-1] for row in matrix] 使用列表推导式，进行左右翻转。最终得到结果

总结一下，由于找规律的方式时间复杂度较高，防止我们螺旋矩阵操作期间超时，我们使用转置＋翻转的方式。

三、翻转矩阵进行输出

回到我们的题目中，我们需要将剔除的第一行进行输出，然后进行对整体顺时针翻转，然后重复这样的操作即可。

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        res = []
        while matrix:
            res += matrix.pop(0)
            matrix = list(map(list,zip(*matrix)))[::-1]
        return res

第一次写这种文章。请多见谅。