目录
1.我们以一个 4×4 像素 的 8-bit 灰度图为例,展示像素值及其直方图均衡化的计算过程。
1、灰度变换(点运算)
1.线性点运算
像素点运算的灰度值的变换过程是线性变换,通常使用线性公式来表示:
其中,s为输出灰度值,r为输入灰度值,a与b为变换系数。呈线性变换关系
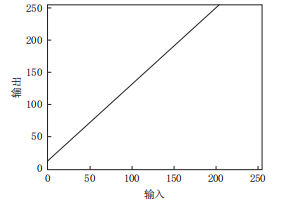
根据线性函数中,a为斜率,b为偏置,我们可以作类比讨论。我们这里稍后讨论b对整个图像的影响,这里首先着重注意a对图像的影响。当a > 1时,斜率增大,输入对应的输出将会以a倍增大,因此图像的对比度将增大(我们可以理解定下某两个点之后,经过线性变换后灰度值的差距增大)同理,当0< a <1时,图像的对比度降低。那么a = 1时,原输入对应原输出。这两种情况均是仍成正相关问题。
接下来我们将引入b进行讨论。当b = 0时,图像不会整体的发生改变,当b > 0,图像整体灰度值增大,呈现亮的效果;当b < 0 时,呈现整体变暗的效果。
我们在这里就应该注意到,我们这样的进行计算,难免会造成原输入的位置经过变换后超过最大值255或小于最小值0,这里我们将对超过与小于的部分进行截断操作。(这里先不考虑失真问题)
有了这个知识,我们可以讨论当a < 0 的情况了,我们设置b为正值,那么整个图像灰度值将从b开始权重为a进行下降,对应位置具有翻转亮度的效果。
总结一下,
(1)当a=1,b=0时,输入和输出相等,即输出原图像。
(2)当a=1,b>0时,输出灰度值变大,图像整体变亮。
(3)当a=1,b<0时,输出灰度值变小,图像整体变暗。
(4)当a>1时,输出图像对比度增大。
(5)当0<a<1时,输出图像对比度减小。
(6)当a<0时,图像暗区变亮,亮区变暗,完成图像求补。
因此我们可以进行代码撰写:
import matplotlib.pyplot as plt
import cv2
import numpy as np
# 读取图像
img = cv2.imread('001.bmp', 0) # 读取灰度图像
# 将图像转换为浮点型,以便进行乘法操作
img = img.astype(np.float32)
# 定义参数和子图
params = [
(1, 0, 'a=1,b=0'),
(1, 50, 'a=1,b=50'),
(1, -50, 'a=1,b=-50'),
(1.5, 0, 'a=1.5,b=0'),
(0.3, 0, 'a=0.3,b=0'),
(-1, 0, 'a=-1,b=0')
]
# 显示图像
for i, (a, b, title) in enumerate(params):
img1 = a * img + b # 直接使用 NumPy 的广播机制
plt.subplot(2, 3, i + 1)
plt.imshow(img1, cmap='gray', vmin=0, vmax=255)
plt.title(title)
plt.axis() # 关闭坐标轴
# 显示所有图像
plt.show()我们在这里为方便起见,使用列表存储每一个元组,元组中存储的分别是a、b的数值以及将要画图使用的title。

2.非线性运算
非线性运算分为对数运算与幂次运算,对数运算公式如下:
其中,s为灰度值,c为常数,默认先灰度值都大于或等于0,对数变换可以将灰度值低的区域进行拉伸,使图像暗区的灰度值增大,提高图像的亮度。
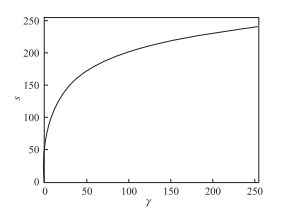
幂次运算的公式如下:
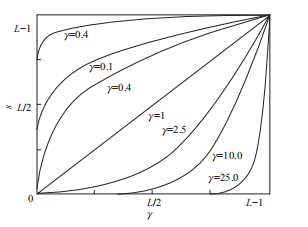
其中,s为输出灰度值,r为输入灰度值,c和γ为正常数。幂次变换比对数变换更为复杂,根
据γ值的不同,幂次变换会得到不同的结果。γ值以1为分界线,当值大于1时可以产生和对数运
算相同的结果,即将灰度值低的区域进行扩展,灰度值高的区域进行压缩,提高图像亮度。当γ值
小于1时,将得到相反的结果,即灰度值高的区域进行扩展,将灰度值低的区域进行压缩,减小图
像亮度。当c=γ=1是,将是简单的线性变换,输入与输出相等。图中给出了c=1时,γ取不
同值时的幂次变换曲线。从中可以看出,随着γ 不断增大,变换结果逐渐由加亮减暗变成加暗
减亮。
代码实现如下:
import cv2
import matplotlib.pyplot as plt
import numpy as np
# 读取图像并归一化到 [0, 1]
img = cv2.imread('001.bmp', 0) # 读取灰度图像
if img is None:
print("Error: Image not loaded. Check the file path.")
exit()
img = img / 255.0 # 归一化到 [0, 1]
# 显示原始图像
plt.subplot(231)
plt.imshow(img, 'gray')
plt.title('Original')
# 设置参数
param = [0.1, 0.4, 1, 2.5, 1]
c = 1
# 遍历参数并绘制子图
for i, r in enumerate(param):
plt.subplot(2, 3, i + 2) # 子图位置
temp = cv2.pow(img, r) # 计算幂运算
temp = np.clip(temp, 0, 1) # 确保输出值在 [0, 1] 范围内
plt.imshow(temp, 'gray')
plt.title(f'c={c}, r={r}') # 格式化标题
# 显示所有图像
plt.show()-
图像数据通常是
uint8类型(0~255),但cv2.pow()等运算可能会导致数值爆炸(如255^2.5非常大)。 -
归一化到 [0, 1] 后,幂运算
img^r的结果仍然保持在合理范围内(如1^2.5 = 1),避免数值溢出或计算不稳定。
2.图像代数运算
首先我们如果想实现对图像代数运算,为了使效果明显,我们首先需要对图片进行加噪,代码如下
# 定义高斯噪声函数
def GaussianNoise(image, mean, stddev):
"""
给图像加高斯噪声
:param image: 输入图像
:param mean: 噪声均值
:param stddev: 噪声标准差
:return: 加噪声后的图像
"""
row, col = image.shape
gauss = np.random.normal(mean, stddev, (row, col))
noisy = image + gauss
noisy = np.clip(noisy, 0, 1) # 保证像素值在[0, 1]之间
return noisy
1.加法运算
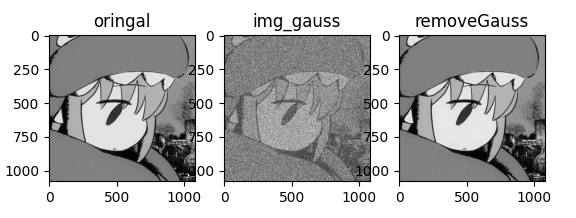
加法运算通常用来去除加性噪声,因为当噪声可以用一个独立分布的随机模型表示和描述时,就可以利用平均值方法减低信号的噪声。假设当前存在某个静止场景或物体的多幅图片集合,如果这些图片都被随机噪声干扰,那就可使用加法进行一定程度的去噪。 公式如下:

这三张图片分别是,叠加高斯噪声的灰度图像 、4幅图像叠加平均的结果、8幅图像叠加平均的结果
代码实现:(假设已经经过高斯噪声函数)
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 加载图像并转换为灰度图
img = cv2.imread('001.bmp', 0) # 读取图像,0表示灰度图
# 将图像转换为NumPy数组并使其可修改
img = np.array(img)
img.flags.writeable = True
# 将像素值归一化到[0, 1]之间
img = img / 255.0
# 给图像添加高斯噪声
img_n = GaussianNoise(img, 0, 1)
# 绘制原图、带噪声图和去噪后的图像
plt.subplot(131)
plt.imshow(img, cmap='gray')
plt.title('oringal')
plt.subplot(132)
plt.imshow(img_n, cmap='gray')
plt.title("img_gauss")
# 多次加噪声并平均化以去噪
k = np.zeros([img.shape[0], img.shape[1]])
for i in range(100):
j = GaussianNoise(img, 0, 0.05)
k = k + j
k = k / 100 # 计算平均值以去除噪声
plt.subplot(133)
plt.imshow(k, cmap='gray')
plt.title('removeGauss')
# 显示图像
plt.show()
2.减法运算
加法与减法相反,减法表达式如下所示:
常用来检测变化和运动的物体,又称差分运算。将同一景物不同时间拍摄的图像进行减法运算,可以实现对该区域的动态监测、运动目标检测和跟踪等操作。
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('001.bmp',0)
img = img/255
img_n = GaussianNoise(img,0.1,0.05)
K = img_n - img
plt.subplot(131)
plt.imshow(img_n,'gray')
plt.title('equipGauss')
plt.subplot(132)
plt.imshow(img,'gray')
plt.title('oringal')
plt.subplot(133)
plt.imshow(K,'gray')
plt.title('Gauss')
plt.show()
3.乘法运算
乘法运算能够实现灰度值的改变,达到修改图像亮度的目的。乘法也可以用来获得掩模图 像,将所需要留下的区域设置为1,将不需要保留的区域设置为0,这样就能够通过乘法运算获取 图像的目标区域。同时,乘法运算也经常用来实现卷积或相关处理。以下为代码实现:
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('001.bmp', 0) # 读取灰度图 (0~255, uint8)
img_float = img.astype(np.float32) # 转为 float 避免溢出
img1 = np.clip(1.2 * img_float, 0, 255).astype(np.uint8) # 限制在 [0, 255]
img2 = np.clip(2 * img_float, 0, 255).astype(np.uint8)
plt.subplot(131)
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.title('Original')
plt.subplot(132)
plt.imshow(img1, cmap='gray', vmin=0, vmax=255)
plt.title('Multiply 1.2')
plt.subplot(133)
plt.imshow(img2, cmap='gray', vmin=0, vmax=255)
plt.title('Multiply 2')
plt.show()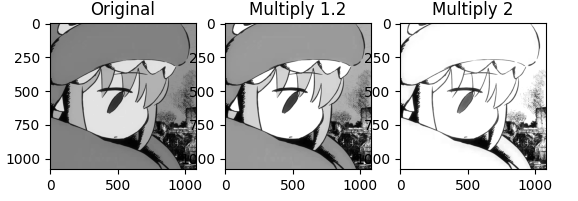
4.除法运算
除法运算也可以改变像素的灰度值,调整图像亮度。也能够用来校正成像设备的非线性影响,常在CT等医学图像中用到。以下是代码实现:
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('001.bmp', 0) # 读取灰度图 (0~255, uint8)
img_float = img.astype(np.float32) # 转为 float 避免精度丢失
img1 = (img_float / 2).astype(np.uint8) # 除以 2
img2 = (img_float / 4).astype(np.uint8) # 除以 4
img3 = (img_float / 8).astype(np.uint8) # 除以 8
plt.subplot(141)
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.title('Original')
plt.subplot(142)
plt.imshow(img1, cmap='gray', vmin=0, vmax=255)
plt.title('Divide 2')
plt.subplot(143)
plt.imshow(img2, cmap='gray', vmin=0, vmax=255)
plt.title('Divide 4')
plt.subplot(144)
plt.imshow(img3, cmap='gray', vmin=0, vmax=255)
plt.title('Divide 8')
plt.show()
3.灰度直方图
灰度直方图是图像灰度级分布的函数,是对灰度分布的统计。灰度直方图将图像中所有像素点按照其灰度级的大小,统计每个值出现的频率,可以用公式表示为
其中,n是像素点的个数,nk 是k级像素点的个数,且满足:
灰度直方图反映图像灰度出现频率的分布,并不是具体位置的分布,一共图像只能存在一共灰度直方图。其中,n是像素点的个数,nk 是k级像素点的个数,且满足
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('./image/football.jpg',0)
plt.subplot(131)
plt.imshow(img,'gray')
plt.title('oringal')
plt.subplot(132)
hist = cv2.calcHist([img],[0],None,[256],[0,255])
plt.plot(hist)
plt.title('hist1')
plt.subplot(133)
plt.hist(img.ravel(),256,[0,256])
plt.title('hist2')
plt.show()
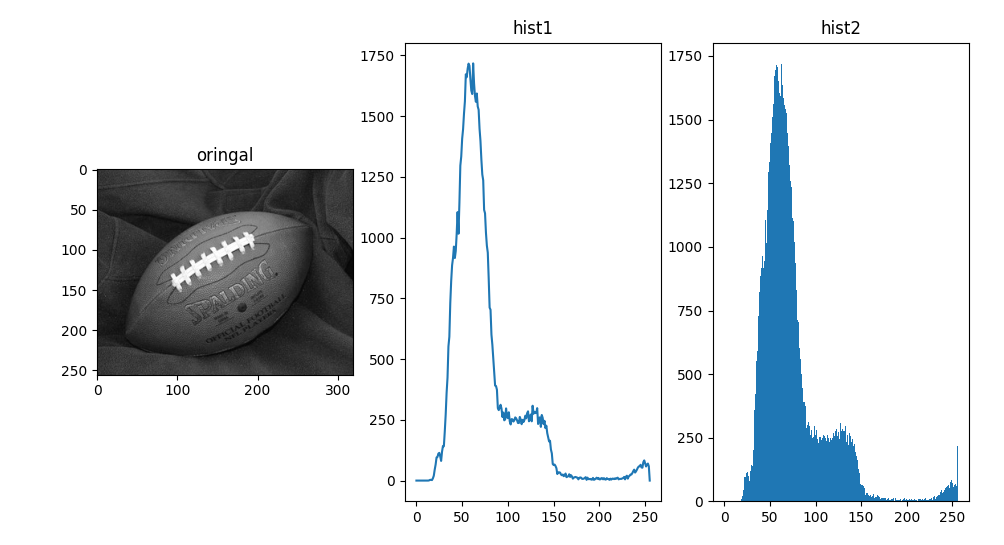
4.直方图均衡化
直方图均衡化:主要用于增强动态范围偏小的图像的反差(对比度),使图像更加清晰。
基本思想是把原始图的直方图变换为在整个灰度范围内均匀分布的形式,增加像素灰度值的动态范围,从而达到增强图像整体对比度的效果。

直方图窄 --> 直方图宽
要把很窄的直方图变成很宽的直方图,需要一个拉伸函数。显而易见,这个函数必须保证图像中原有像素的灰度值顺序不能变,否则会改变原图像表达的内容。这时候我们想到了累积分布函数。
均衡化的数学原理
均衡化的本质是 像素值的非线性映射,使得输出图像的直方图近似 均匀分布。
(1) 计算原始直方图
统计每个灰度级 如0,1,2,…,255)的像素数量
,并计算概率:
,N=图像总像素数
(2) 计算累积分布函数(CDF)
CDF 表示灰度级 ≤ 的像素占比:
CDF 是一个单调递增函数,范围在 [0, 1]。
(3) 映射到新的灰度级
将 CDF 线性映射到 0~255 范围,得到新的灰度级:
示例:
1.我们以一个 4×4 像素 的 8-bit 灰度图为例,展示像素值及其直方图均衡化的计算过程。
50 70 90 110 70 100 120 130 90 120 140 150 110 130 150 100
假设图像较暗,像素集中在低灰度区(50~150)
2.计算直方图
| 灰度值 | 像素数量 | 概率 |
| 50 | 1 | 1/16 ≈ 0.0625 |
| 70 | 2 | 2/16 = 0.125 |
| 90 | 2 | 2/16 = 0.125 |
| 100 | 2 | 2/16 = 0.125 |
| 110 | 2 | 2/16 = 0.125 |
| 120 | 2 | 2/16 = 0.125 |
| 130 | 2 | 2/16 = 0.125 |
| 140 | 1 | 1/16 ≈ 0.0625 |
| 150 | 2 | 2/16 = 0.125 |
3. 计算累积分布函数(CDF)
| 灰度级 | ||
|---|---|---|
| 50 | 0.0625 | 0.0625 |
| 70 | 0.125 | 0.0625 + 0.125 = 0.1875 |
| 90 | 0.125 | 0.1875 + 0.125 = 0.3125 |
| 100 | 0.125 | 0.3125 + 0.125 = 0.4375 |
| 110 | 0.125 | 0.4375 + 0.125 = 0.5625 |
| 120 | 0.125 | 0.5625 + 0.125 = 0.6875 |
| 130 | 0.125 | 0.6875 + 0.125 = 0.8125 |
| 140 | 0.0625 | 0.8125 + 0.0625 = 0.8750 |
| 150 | 0.125 | 0.8750 + 0.125 = 1.0000 |
4. 将CDF映射到新灰度级(0~255)
| 灰度级 | 新灰度值 | |
|---|---|---|
| 50 | 0.0625 | round(0.0625×255) = 16 |
| 70 | 0.1875 | round(0.1875×255) = 48 |
| 90 | 0.3125 | round(0.3125×255) = 80 |
| 100 | 0.4375 | round(0.4375×255) = 112 |
| 110 | 0.5625 | round(0.5625×255) = 143 |
| 120 | 0.6875 | round(0.6875×255) = 175 |
| 130 | 0.8125 | round(0.8125×255) = 207 |
| 140 | 0.8750 | round(0.8750×255) = 223 |
| 150 | 1.0000 | round(1.0000×255) = 255 |
5. 均衡化后的图像
将原始像素替换为映射后的值:
16 48 80 112 48 112 143 175 80 175 223 255 112 207 255 112
代码实现
import cv2
import matplotlib.pyplot as plt
# 读取灰度图像
img = cv2.imread('001.bmp', 0)
# 图像变亮(增加像素值)
img_h = cv2.add(img, 150)
# 图像变暗(降低像素值)
img_l = cv2.multiply(img, 0.2)
# 计算变亮/变暗后的直方图
img_h_t = cv2.calcHist([img_h], [0], None, [256], [0, 256])
img_l_t = cv2.calcHist([img_l], [0], None, [256], [0, 256])
# 对变亮/变暗图像进行直方图均衡化
img_h_h = cv2.equalizeHist(img_h)
img_l_h = cv2.equalizeHist(img_l)
# 计算均衡化后的直方图
img_h_l = cv2.calcHist([img_h_h], [0], None, [256], [0, 256])
img_l_l = cv2.calcHist([img_l_h], [0], None, [256], [0, 256])
# 显示图像和直方图(2行4列布局)
plt.subplot(241)
plt.imshow(img_h, 'gray')
plt.title('lighter')
plt.subplot(242)
plt.imshow(img_h_h, 'gray')
plt.title('after_equal')
plt.subplot(245)
plt.plot(img_h_t, 'gray')
plt.title('lighterHist')
plt.subplot(246)
plt.plot(img_h_l, 'gray')
plt.title('afterEqualHist')
plt.subplot(243)
plt.imshow(img_l, 'gray')
plt.title('darker')
plt.subplot(244)
plt.imshow(img_l_h, 'gray')
plt.title('afterEqualHist')
plt.subplot(247)
plt.plot(img_l_t, 'gray')
plt.title('darkerHist')
plt.subplot(248)
plt.plot(img_l_l, 'gray')
plt.title('AfterEqual')
plt.show()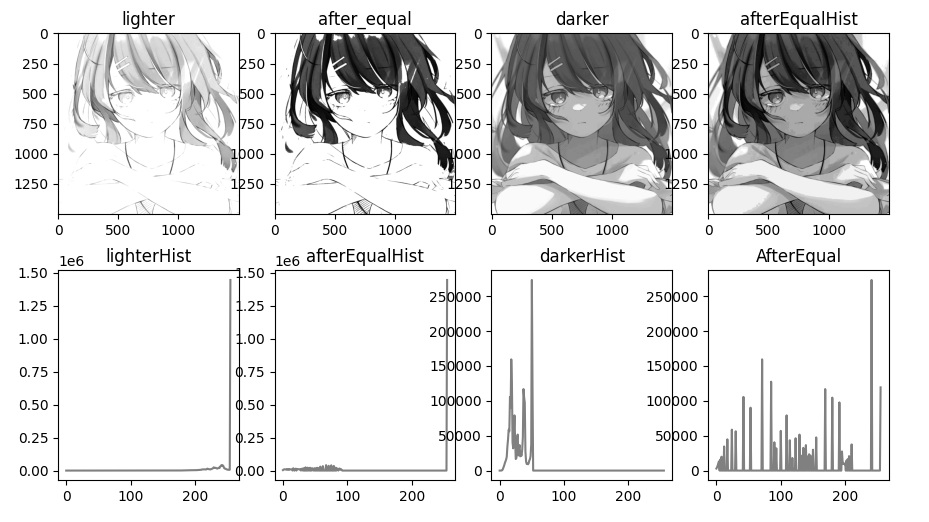
最后我们可以看出:部分区域过亮或过暗。噪声被放大(如原本较暗区域的噪声变得明显)




















 388
388

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








