python 函数

循环结构

for-in循环

• range(101)可以产生一个0到100的整数序列。
• range(1, 100)可以产生一个1到99的整数序列。
• range(1, 100, 2)可以产生一个1到99的奇数序列，其中的2是步长，即数值序列的增量。

知道了这一点，我们可以用下面的代码来实现1~100之间的偶数求和。

#用for循环实现1~100之间的偶数求和
sum = 0
for x in range(2, 101, 2):
    sum += x
print(sum)

也可以通过在循环中使用分支结构的方式来实现相同的功能

#用for循环实现1~100之间的偶数求和

sum = 0
for x in range(1, 101):
    if x % 2 == 0:
        sum += x
print(sum)

如果要构造不知道具体循环次数的循环结构，我们推荐使用while循环，while循环通过一个能够产生或转换出bool值的表达式来控制循环，表达式的值为True循环继续，表达式的值为False循环结束。

while循环

#while结构
while condition:
    ........
 
i = 0
while i < 10:
    print(i)
    i += 1

#猜数字游戏
#计算机出一个1~100之间的随机数由人来猜
#计算机根据人猜的数字分别给出提示大一点/小一点/猜对了
import random

answer = random.randint(1, 100)
counter = 0
while True:
    counter += 1
    number = int(input('请输入: '))
    if number < answer:
        print('大一点')
    elif number > answer:
        print('小一点')
    else:
        print('恭喜你猜对了!')
        break
print('你总共猜了%d次' % counter)
if counter > 7:
    print('你的智商余额明显不足')

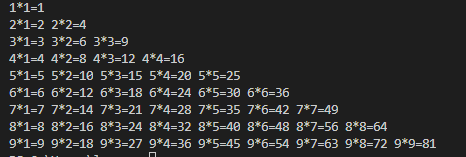
#输出乘法口诀表(九九表)
number=1
for i in range(1,10):
    for j in range(1,i+1):
        print('%d*%d=%d'%(i,j,i*j),end=' ')   #end = “ ”的意思就是在每个计算的结尾处加个空格
    print(' ')

函数

在Python中可以使用def关键字来定义函数，和变量一样每个函数也有一个响亮的名字，而且命名规则跟变量的命名规则是一致的。在函数名后面的圆括号中可以放置传递给函数的参数

def defineName([params]):
    ...........
    ...........
    return .....
 调用:
 	defineName([params])
 """

函数的参数

在Python中，函数的参数可以有默认值，也支持使用可变参数，所以Python并不需要像其他语言一样支持函数的重载

from random import randint


def roll_dice(n=2):
    """
    摇色子
    :param n: 色子的个数
    :return: n颗色子点数之和
    """
    total = 0
    for _ in range(n):
        total += randint(1, 6)
    return total

带默认值的参数一定要统一放在最后!

def add(a=0, b=0, c=0):
    return a + b + c
# 如果没有指定参数那么使用默认值摇两颗色子
print(roll_dice())
# 摇三颗色子
print(roll_dice(3))
print(add())
print(add(1))
print(add(1, 2))
print(add(1, 2, 3))
# 传递参数时可以不按照设定的顺序进行传递
print(add(c=50, a=100, b=200))

我们给上面两个函数的参数都设定了默认值，这也就意味着如果在调用函数的时候如果没有传入对应参数的值时将使用该参数的默认值
我们可以用各种不同的方式去调用add函数

# 在参数名前面的*表示args是一个可变参数(不定长参数)
# 即在调用add函数时可以传入0个或多个参数
def add(*args):
    total = 0
    for val in args:
        total += val
    return total


print(add())
print(add(1))
print(add(1, 2))
print(add(1, 2, 3))
print(add(1, 3, 5, 7, 9))

练习

``实现计算求最大公约数和最小公倍数的函数。

def gcd(x, y):
    (x, y) = (y, x) if x > y else (x, y)
    for factor in range(x, 0, -1):
        if x % factor == 0 and y % factor == 0:
            return factor
def lcm(x, y):
    return x * y // gcd(x, y)