FDTD中的复杂材料

前言

自然界中很多材料由于自身的物理性质导致它们与电磁波相互作用时会产生一些复杂的光学效应。当光在材料中的速度随频率变化较大时，该材料就被称为色散材料。

在前面的文章中，我们介绍了时域有限差分（FDTD）算法求解的是麦克斯韦方程组的时域解，通过傅里叶变换在一次仿真中就可以得到器件在宽频中的响应特性。因此，在FDTD仿真中，无法将不同频率的材料散点数据直接应用在宽频求解中，必须对散点的测试数据进行准确建模，然后通过线性循环卷积算法，或者色散材料Z变换，或者色散辅助方程等方法处理色散材料。本文将介绍几种FDTD算法中常用的复杂材料模型。

本构关系和色散材料

电通量密度和电场，磁场和磁通量，有如下关系：
$$D={ϵ}_{0}E+P\text{\hspace{1em}(1)}$$
$$H=\frac{B}{{\mu }_0}-M\text{\hspace{1em}(2)}$$
在一个给定频率上，对于一个线性各向同性介质，极化矢量可以表示为：
$$\hat{P}(\omega )={ϵ}_0{\hat{\chi }}_e(\omega )\hat{E}(\omega )\text{\hspace{1em}(3)}$$
$$\hat{M}(\omega )={\hat{\chi }}_m(\omega )\hat{H}(\omega )\text{\hspace{1em}(4)}$$
其中${\hat{\chi }}_e(\omega )$和${\hat{\chi }}_m(\omega )$分别是电极化率和磁极化率。因此，可以得到
$$\hat{D}(\omega )={ϵ}_0\hat{E}(\omega )+{ϵ}_0{\hat{\chi }}_e(\omega )\hat{E}(\omega )\text{\hspace{1em}(5)}$$
$$\hat{B}(\omega )={\mu }_0\hat{H}(\omega )+{\mu }_0{\hat{\chi }}_m(\omega )\hat{H}(\omega )\text{\hspace{1em}(6)}$$
这里我们只讨论非磁性材料，其中介电常数$\widehat{ϵ}(\omega )$定义为
$$\widehat{ϵ}(\omega )={ϵ}_0{\widehat{ϵ}}_r(\omega )={ϵ}_0({ϵ}_{\infty }+{\hat{\chi }}_e(\omega ))\text{\hspace{1em}(7)}$$
其中${\widehat{ϵ}}_r$是相对介电常数，常数${ϵ}_{\infty }$说明了在极高频率时带电材料趋于的相对介电常数。

在FDTD中运用辅助差分方程方法（Auxiliary Differential equation, ADE），将极化和电场联系起来的微分方程进行有限差分近似，可以根据过去的极化值和电场计算得到未来时刻的极化值。所以只要有了材料的极化率表达式，我们就可以将其加入到FDTD的迭代过程中。

Drude材料模型

Drude材料模型通常适用于金属。在该模型中，假定电荷在电场的影响下运动，但它们也会受到阻尼力的作用。可以通过下面的简单力学模型来描述：
$$M\frac{d^{2}x}{d{t}^2}=QE(t)-M{\gamma }_p\frac{dx}{dt}\text{\hspace{1em}(8)}$$
其中，$M$是电荷的质量、${\gamma }_p$是阻尼系数、$Q$是带电量、$x$是电荷的位移（位移被假设为在任意方向上，不限于x轴）。等式的左边是质量乘以加速度，右边是作用在电荷上的合力，即驱动力和阻尼力。重新整理并转化到频域得到：
$$M(j\omega {)}^2\hat{x}(\omega )+M{\gamma }_p(j\omega )\hat{x}(\omega )=Q\hat{E}(\omega )\text{\hspace{1em}(9)}$$
因此，位移可以表示成
$$\hat{x}(\omega )=-\frac{Q}{M({\omega }^2-j{\gamma }_p\omega )}\hat{E}(\omega )\text{\hspace{1em}(10)}$$
极化矢量$P$与单个电荷的偶极矩有关。如果$N$是单位体积内的偶极子数目，极化矢量为
$$\hat{P}=NQ\hat{x}\text{\hspace{1em}(11)}$$
注意，$P$的单位是库伦每平方米$(C/m^2)$，与电通量单位相同。对比式（10）和式（11），可以得到
$$\hat{P}(\omega )=-{ϵ}_0\frac{\frac{N{Q}^2}{M{ϵ}_0}}{{\omega }^2-j{\gamma }_p\omega }\hat{E}(\omega )\text{\hspace{1em}(12)}$$
因此，Drude材料的电极化率为
$$\widehat{{\chi }_e}(\omega )=-\frac{{\omega }_p^2}{{\omega }^2-j{\gamma }_p\omega }\text{\hspace{1em}(13)}$$
其中${\omega }_p^2=N{Q}^2/(M{ϵ}_0)$。然而，我们并不关心一个常量背后的细节，因此Drude材料的相对介电常数通常可以写为
$$\widehat{{ϵ}_r}(\omega )={ϵ}_{\infty }-\frac{{\omega }_p^2}{{\omega }^2-j{\gamma }_p\omega }\text{\hspace{1em}(14)}$$
注意到，随着$\omega$趋近于无穷，相对介电常数会趋近于${ϵ}_{\infty }$。对式（13）做逆傅里叶变换可以得到Drude模型材料的脉冲响应：
$${\chi }_e(t)=\frac{{\omega }_p^2}{{\gamma }_p}(1-e^{-{\gamma }_{p}t})u(t)\text{\hspace{1em}(15)}$$
其中$u(t)$是单位阶跃函数。因子${\gamma }_p$是弛豫时间的倒数。

下图展示了一个使用Drude模型构建的银材料，它的材料参数设置为${ϵ}_{\infty }=1$、${\omega }_p=1.37e+16$、${\gamma }_p=8.5e+13$。

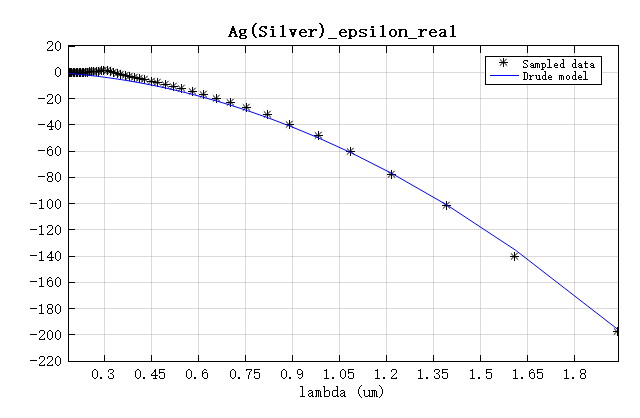
从图中可以看出使用Drude模型构建的银材料与其实验测得的散点数据非常接近。具体请参考SimWorks的案例
等离子超材料红外吸收器

Lorenz材料模型

Lorenz材料是基于电荷运动的二阶力学模型。在这种情况下，除了一个阻尼力，还有一个回复力（使电荷回到初始位置的弹力）。合力的表达式为
$$M\frac{d^{2}x}{d{t}^2}=QE(t)-M{\gamma }_p\frac{dx}{dt}-MKx\text{\hspace{1em}(16)}$$
前三项与式（8）中具有相同的含义。其他项代表回复力（与位移成正比）且与弹性系数$K$成正比。转换到频域并重新整理得到
$$-M{\omega }^2\hat{x}(\omega )+jM{\gamma }_p\omega \hat{x}(\omega )+MK\hat{x}(\omega )=Q\hat{E}(\omega )\text{\hspace{1em}(17)}$$
因此，位移表达式为
$$\hat{x}(\omega )=\frac{Q}{M(K+j{\gamma }_p\omega -{\omega }^2)}\hat{E}(\omega )\text{\hspace{1em}(18)}$$
与Drude模型类似，可以推出Lorentz材料的电极化率为
$${\hat{\chi }}_e(\omega )=\frac{{ϵ}_p{\omega }_p^2}{{\omega }_p^2+2j{\gamma }_p\omega -{\omega }^2}\text{\hspace{1em}(19)}$$
其中${\omega }_p$是无阻尼共振频率，${\gamma }_{p}R$是阻尼系数，${ϵ}_p$代表由于洛伦兹振子引入的介电常数的变化（频率接近无穷的介电常数 减 零频介电常数）。相对应的相对介电常数由下式给出
$${\widehat{ϵ}}_r(\omega )={ϵ}_{\infty }+\frac{{ϵ}_p{\omega }_p^2}{{\omega }_p^2+2j{\gamma }_p\omega -{\omega }^2}\text{\hspace{1em}(20)}$$
下图展示了一个使用Lorentz模型构建的硅材料，它的参数设置为${ϵ}_{\infty }=7.98737492$、${ϵ}_p=3.68799143$、${\omega }_p=3.93282466e+15$、${\gamma }_p=1e+8$，以匹配1.15至1.8$\mu m$范围内的硅材料数据（来自Palik手册）。

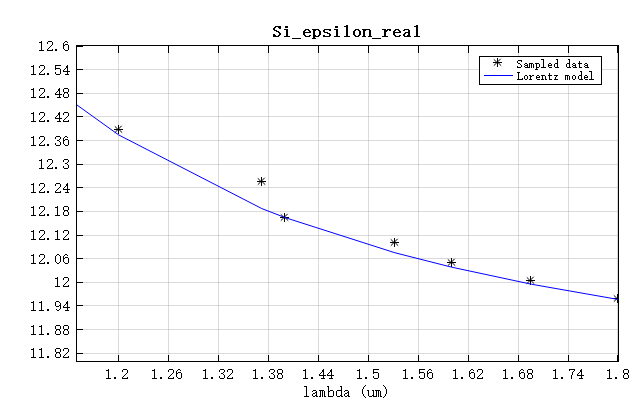
从图中可以看到使用Lorentz模型构建的硅材料与实验数据非常接近。请参考SimWorks的案例：基于FDTD的布拉格光栅

Debye材料模型

Debye材料可以被看作是一个简单的RC电路，其中极化量与电容两端的电压有关。驱动电路的源是电场。对于在该源中的一个步骤，有可能存在固定极化。当频率趋近无穷大时，极化量趋近于零（只剩下常数留数的高频分量）。因此电极化矢量为
$${\hat{\chi }}_e(\omega )=\frac{\Delta {ϵ}_p}{1+j\omega {\gamma }_p}\text{\hspace{1em}(21)}$$
其中${\gamma }_p$是弛豫时间系数，$\Delta {ϵ}_p$是由于德拜振子引入的介电常数的变化（频率接近无穷的介电常数减零频介电常数）。相对介电常数的表达式为
$${\widehat{ϵ}}_r(\omega )={ϵ}_{\infty }+\frac{\Delta {ϵ}_p}{1+j\omega {\gamma }_p}\text{\hspace{1em}(22)}$$

RDFM材料模型

RDFM材料模型全称为有理分数色散材料模型(Rational-Fraction Dispersive Model)。采用RFDM来描述色散材料的相对介电常数，用有理分数形式表示为
$${ϵ}_r(\omega )=\frac{\sum _{k=1}^N{a}_k(j\omega {)}^k}{\sum _{k=1}^N{b}_k(j\omega {)}^k}\text{\hspace{1em}(23)}$$
其中$a_k$和$b_k$是一系列的实数。有理分数形式是两个多项式和的比，其中分母的最高阶与分子的最高阶相同。这两个多项式的参数和可以通过有理近似法准确快速地估算出来。为了便于FDTD算法使用，RFDM模型采用部分分数展开表示为：
$${ϵ}_r(\omega )={ϵ}_{\infty }+\sum _{k=1}^L{\chi }_k(\omega )\text{\hspace{1em}(24)}$$
其中
$${\chi }_k(\omega )=\{\begin{array}{l}\frac{r_k}{j\omega -p_k}\\ \sum _k\frac{r_k}{j_{\omega }-p_k}+\frac{r_k^{\ast }}{j\omega -p_k^{\ast }}\end{array}\text{\hspace{1em}(25)}$$
对比式（24）与式（15）、式（20）和式（22），可以发现Drude、Lorentz和Debye模型都是RDFM在特定参数下的特例。RFDM模型可以描述任意材料在指定的频率范围内的特性。

SimWorks软件使用RDFM模型来对实验测量得到的材料散点数据进行拟合，通过RDFM模型，将材料的实验数据拟合为稳定的材料模型，如下图。

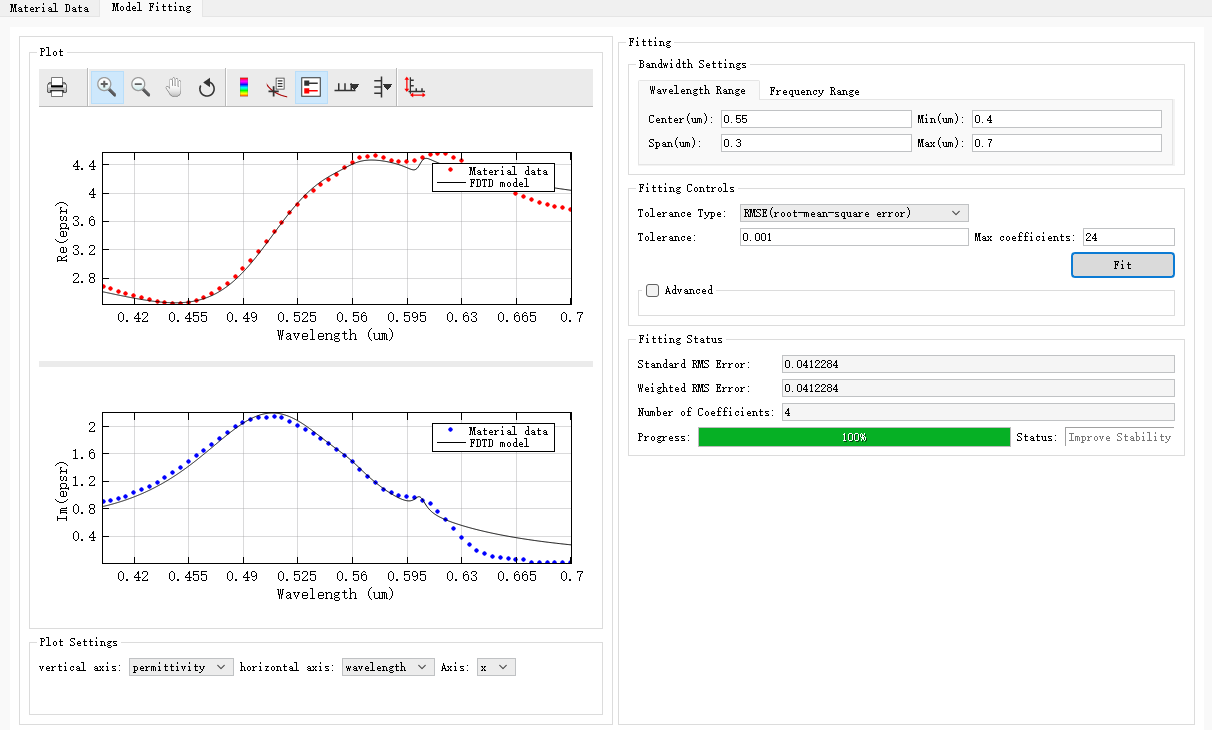
您只需要设置好拟合的频率范围以及以及需要的均方值误差即可。如果拟合模型不满足仿真需求，可以调整多项式最大系数重新拟合。了解更多请见如下链接：具有光子晶体结构的有机太阳能电池

非线性材料

所有材料都具备产生非线性现象的可能，非线性是材料本身的一种属性。一般来说，材料的极化是电场的非线性函数，可表示为
$$P(\omega )={ϵ}_o{\chi }_e^{(1)}(\omega )E(\omega )+{ϵ}_o{\chi }_e^{(2)}(\omega )E^{(2)}(\omega )+{ϵ}_o{\chi }_e^{(2)}(\omega )E^{(2)}(\omega )+...\text{\hspace{1em}(28)}$$
其中，第一项表示材料极化强度的线性响应；后面的项为非线性响应项。

在FDTD中，辅助方程法也可以应用于非线性材料，从而实现对非线性材料的仿真。

二阶非线性材料

二阶非线性材料的极化强度可以写成：
$$P(\omega )={ϵ}_o{\chi }^{(1)}(\omega )E(\omega )+{ϵ}_o{\chi }^{(2)}(\omega )E^{(2)}(\omega )\text{\hspace{1em}(29)}$$
其中${\chi }^{(1)}$为一阶线性极化系数，${\chi }^{(2)}$代为二阶非线性极化系数。了解更多请见如下链接：使用非线性材料产生谐波

三阶非线性材料

在 Kerr 效应或 Raman 散射中，三阶非线性材料的极化强度在时域的定义为：
$$P(t)={ϵ}_0{\chi }^{(1)}E(t)+{ϵ}_0{\chi }^{(2)}{E}^2(t)+{ϵ}_0\alpha {\chi }^{(3)}{E}^3(t)+{ϵ}_0(1-\alpha ){\chi }^{(3)}E(t)\frac{{\omega }_R^2}{{\omega }_R^2-{\omega }^2+2j\omega {\delta }_R}\ast E^2(t)$$
其中，${\omega }_R=\sqrt{\frac{{\tau }_1^2+{\tau }_2^2}{{\tau }_1^2{\tau }_2^2}}$，${\delta }_R=\frac{1}{{\tau }_2}$

三阶非线性材料的参数有6个，分别是：${\chi }_1$一阶线性极化系数、${\chi }_2$二阶非线性计划系数、${\chi }_3$三阶非线性计划系数、$\alpha$ Kerr强度与总的Kerr效应和Raman散射强度的比值、${\tau }_1$特征频率、${\tau }_2$阻尼时间系数。

参考

[1] John B. Schneider, “Understanding the Finite-Difference Time-Domain Method”, www.eecs.wsu.edu/~schneidj/ufdtd, (2010).


[2] Lukas Chrostowsk, Michael Hochberg. Silicon Photonics Design[M], Cambridge University Press, 2015.

[3] Han L. A Rational-Fraction Dispersion Model for Efficient Simulation of Dispersive Material in FDTD Method[J]. Journal of Lightwave Technology: A Joint IEEE/OSA Publication, 2012, 30(13):2216-2225.