HDU 3723 Delta Wave

最新推荐文章于 2019-01-08 08:34:03 发布

原创最新推荐文章于 2019-01-08 08:34:03 发布 · 820 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#hdu #组合数学 #卡特兰数 #排列组合

组合数学专栏收录该内容

5 篇文章

订阅专栏

本文深入探讨了在人类大脑中记录到的高振幅Delta波形，特别是与动漫迷（otaku）群体相关的特殊脑波模式。通过解析从点(0,0)到(N,0)的路径，该文详细解释了如何使用卡特兰数来计算在二维坐标系内形成不同Delta波形的数量。提供了具体示例和算法实现，帮助理解计算过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3723

Delta Wave

Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 1069 Accepted Submission(s): 341

Problem Description

A delta wave is a high amplitude brain wave in humans with a frequency of 1 – 4 hertz which can be recorded with an electroencephalogram (EEG) and is usually associated with slow-wave sleep (SWS).
-- from Wikipedia

The researchers have discovered a new kind of species called "otaku", whose brain waves are rather strange. The delta wave of an otaku's brain can be approximated by a polygonal line in the 2D coordinate system. The line is a route from point (0, 0) to (N, 0), and it is allowed to move only to the right (up, down or straight) at every step. And during the whole moving, it is not allowed to dip below the y = 0 axis.

For example, there are the 9 kinds of delta waves for N = 4:

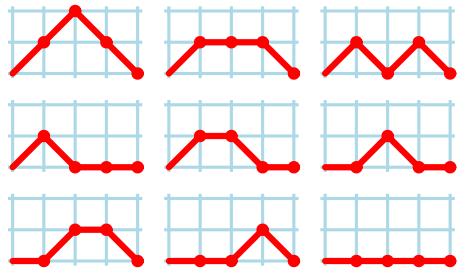
Given N, you are requested to find out how many kinds of different delta waves of otaku.

Input

There are no more than 20 test cases. There is only one line for each case, containing an integer N (2 < N <= 10000)

Output

Output one line for each test case. For the answer may be quite huge, you need only output the answer module 10¹⁰⁰.

Sample Input

3
4

Sample Output

4
9

Source

2010 Asia Tianjin Regional Contest

Recommend

zhouzeyong

思路：坐标是(0,0)和(N,0)，所以向上了几次，就要向下几次。单独考虑向上向下，就是卡特兰数。考虑哪些上哪些下，就是排列组合。

卡特兰数公式：c[n] = c(2n, n) / (n + 1)。
如果上升了 k 次，那么就必须下降 k 次，所以方案数：a[k] = c(n, 2k) * c(2k, k) / (k + 1)，k = 0,1,...,n/2。
因此，总方案数sum[n] = a[0] + a[1] + a[2] + ……+ a[k] (k <= n/2)，且a[0] = 1(只有一个水平的)。
继续化简：a[k] = c(n, 2k) * c(2k, k) / (k + 1) 与 a[k - 1] = c(n, 2k - 2) * c(2k - 2, k - 1) / k，推出下列公式，
a[k] = a[k-1] * (n - 2 * k + 1) * (n - 2 * k + 2) / (k * (k + 1))。数据太大了，所以用Java实现比较方便。

附上AC代码：

import java.util.Scanner;
import java.math.BigInteger;
import java.util.Arrays;
import java.math.BigDecimal;
public class Main{
	public static void main(String args[]){
		Scanner in = new Scanner(System.in);
		while (in.hasNext()){
			int n = in.nextInt();
			BigInteger ans = BigInteger.ONE;
			BigInteger t = BigInteger.ONE;
			for (int i=1; i<=n/2; ++i){
				t = t.multiply(BigInteger.valueOf((n-2*i+1)*(n-2*i+2))).divide(BigInteger.valueOf(i*(i+1)));
				ans = ans.add(t);
			}
			System.out.println(ans.mod(BigInteger.TEN.pow(100)));
		}
		in.close();
	}
}