【数据结构C】 顺序栈和链式栈详解

前言

栈（stack）是限定仅在表尾进行插入或删除操作的线性表。表的尾端有其特殊含义，称为栈顶（top），相应地，表头端称为栈底（bottom/base）。不含元素的空表称为空栈

//顺序栈Init
#include <stdio.h>
#include <stdlib.h>  // 用于malloc

typedef struct {
    int *base;      // 栈底指针
    int *top;       // 栈顶指针
    int stackSize;  // 当前栈容量
} SeqStack;

//链栈Init
#include <stdio.h>
#include <stdlib.h>  // 用于malloc

typedef struct StackNode {
    int data;
    struct StackNode* next;
} StackNode;

typedef struct {
    StackNode* top;  // 栈顶指针
    int size;        // 栈大小（可选）
} LinkedStack;

一、栈的顺序存储结构及其实现

1、顺序栈概念理解

顺序栈（Sequential Stack）是一种基于数组实现的栈结构，采用顺序存储方式，遵循后进先出（LIFO）的原则。下面我们来模拟数组存放数据的情况。

最初，栈是"空栈"，即数组是空的，top、base指向数组的首地址(这种设计让空栈的判断变得非常简单直观，不需要额外标志位)，如下图所示

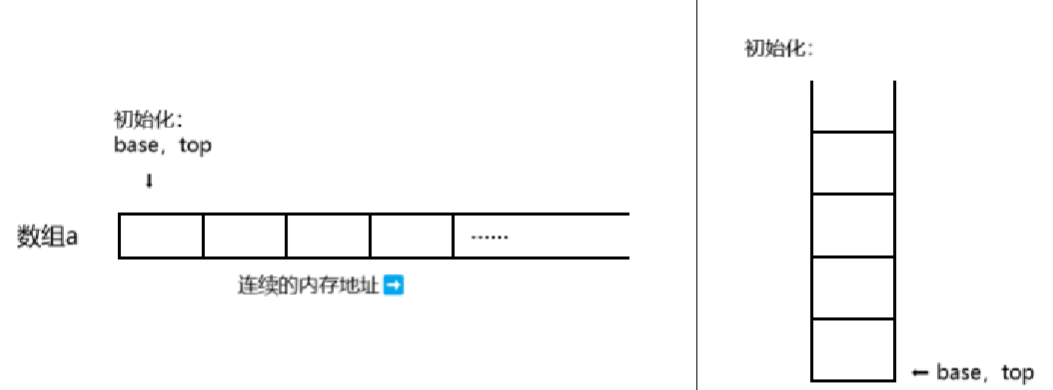
// 初始化栈
void InitStack(SeqStack *S) {
    S->base = (int *)malloc(MAX_SIZE * sizeof(int));
    if (!S->base) exit(1);  // 分配失败退出
    S->top = S->base;
    S->stackSize = 5;
}

if (top == base) // 栈空

向栈中压入元素 10，base指向栈底，给当前top存入10，top++使指针向后移动，如下图所示

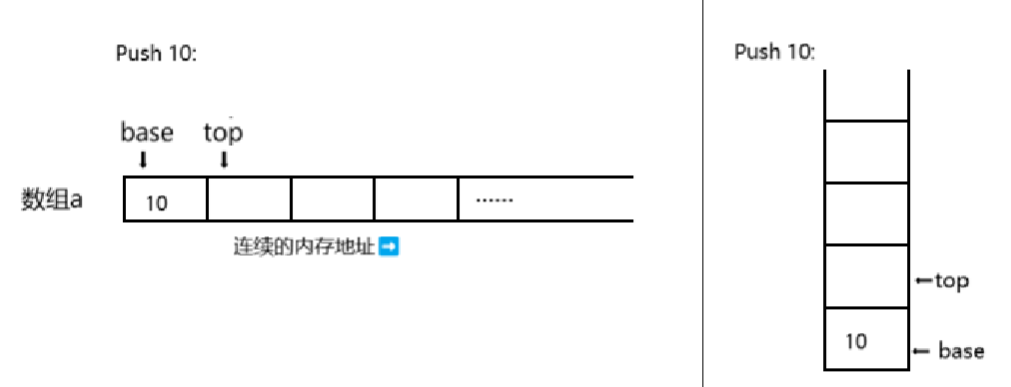
采用以上的方式，依次存储元素 20、30 和 40。base始终指向数组首地址，top总是指向栈顶元素的下一个位置。如下图所示

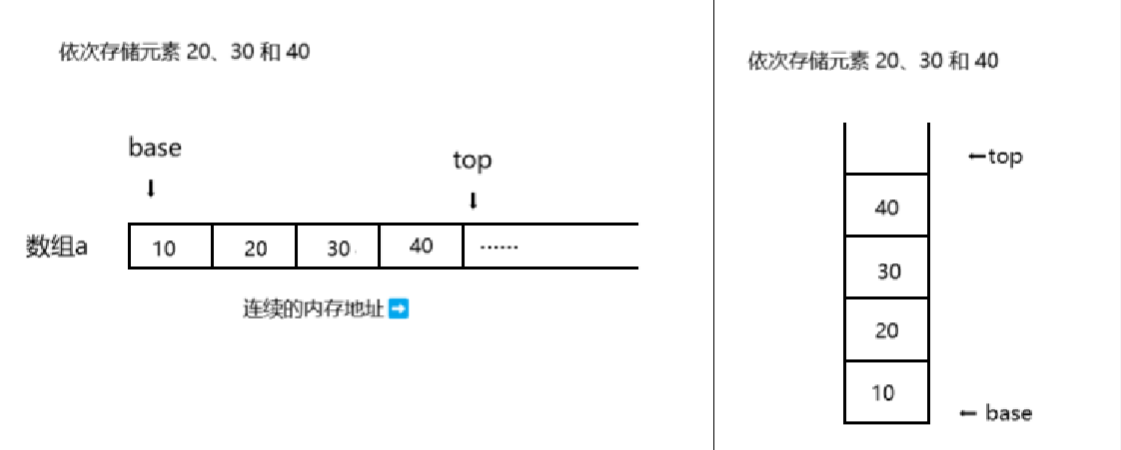
2、入栈（压栈）实现

void StackPush(Stack* ps, STDataType x) {
	assert(ps);
//如果栈满，在原空间后创建新的空间
	if (ps->_top == ps->_capacity) {
		STDataType* tmp = (STDataType*)realloc(ps->_a, sizeof(STDataType) * ps->_capacity * 2);
		if (tmp == NULL) {
			perror("realloc fail");//返回错误信息
			return;
		}

		ps->_a = tmp;
		ps->_capacity *= 2;
	}

	ps->_a[ps->_top] = x;//将元素x压入栈
	ps->_top++;//top指向下一个位置
}

3、出栈（弹栈）实现

移动指针后，原栈顶位置被视为无效数据。这里的出栈是逻辑意义上的出栈，数据还是在原来的地址空间存放。

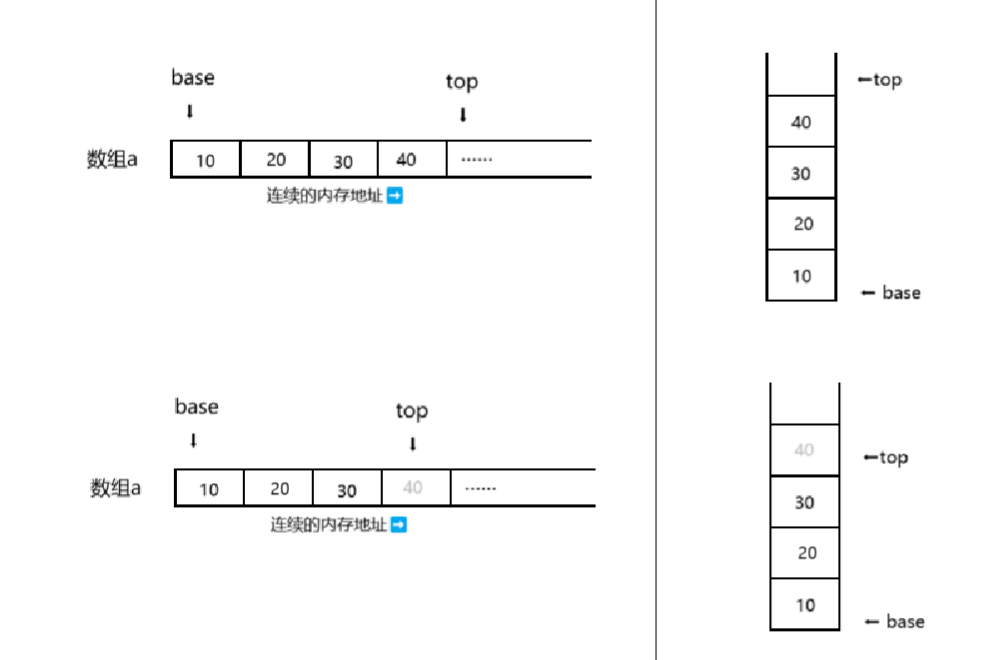
void StackPop(Stack* ps) {
	assert(ps);
	assert(!StackEmpty(ps));//判断是否栈空

	ps->_top--;
}

4、获取栈顶元素

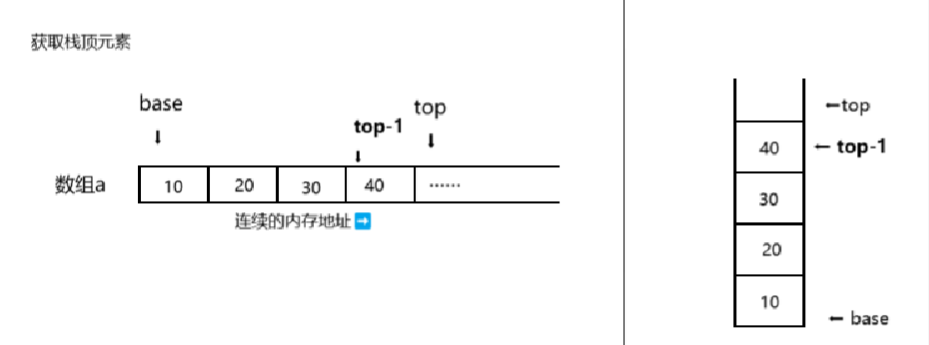
STDataType StackTop(Stack* ps) {
	assert(ps);
	assert(!StackEmpty(ps));

	return ps->_a[ps->_top-1];
}

5、判断栈是否为空

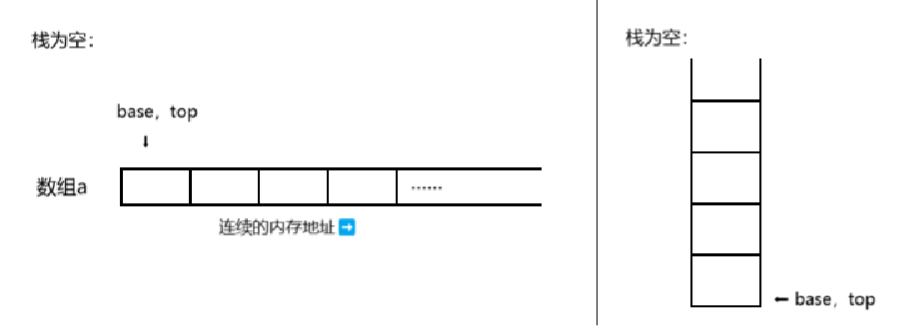
int StackEmpty(Stack* ps) {
	assert(ps);

	return ps->_top == 0;
}

6、销毁栈（malloc创建的空间需要销毁，以便下次使用）

void StackDestroy(Stack* ps) {
	assert(ps);

	free(ps->_a);
	ps->_a = NULL;
	ps->_top = 0;
	ps->_capacity = 0;
}

主函数进行测试

//主函数测试代码
#include <stdio.h>
#include "stack.h"//函数声明和定义均在里面

int main() {
    Stack st;
    
    // 1. 初始化
    StackInit(&st);
    
    // 2. 入栈测试
    StackPush(&st, 10);
    StackPush(&st, 20);
    StackPush(&st, 30);
    
    // 3. 查看栈信息
    printf("Top: %d, Size: %d\n", StackTop(&st), StackSize(&st));
    
    // 4. 出栈测试
    StackPop(&st);
    printf("After pop, Top: %d\n", StackTop(&st));
    
    // 5. 清空栈
    while (!StackEmpty(&st)) {
        printf("Popping: %d\n", StackTop(&st));
        StackPop(&st);
    }
    
    // 6. 销毁
    StackDestroy(&st);
    
    return 0;
}

二、栈的链式存储结构

1、链栈概念理解

链栈（Linked Stack）是一种基于 链表（Linked List） 实现的栈结构，它遵循 后进先出（LIFO, Last In First Out） 的原则。与顺序栈（基于数组）不同，链栈使用 结点（Node） 来动态存储数据，并通过指针链接各个结点。

初始时，链栈为空栈（Empty Stack），此时栈顶指针top指向NULL，表示链表中没有结点，栈的大小为0。【不存在base指针（链栈通常不需要栈底指针，因为链表是动态扩展的）】

将链表的尾部作为栈顶可以避免在“入栈”和“出栈”时的大量操作

 

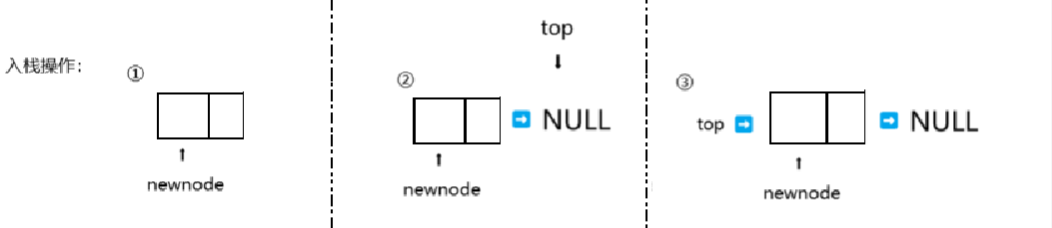
 2、链栈元素入栈

void LStackPush(LinkedStack* S, int elem) {
    StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));
    newNode->data = elem;
    newNode->next = S->top;  // 新节点指向原栈顶
    S->top = newNode;        // 更新栈顶指针
    S->size++;
}

3、链栈元素出栈

 

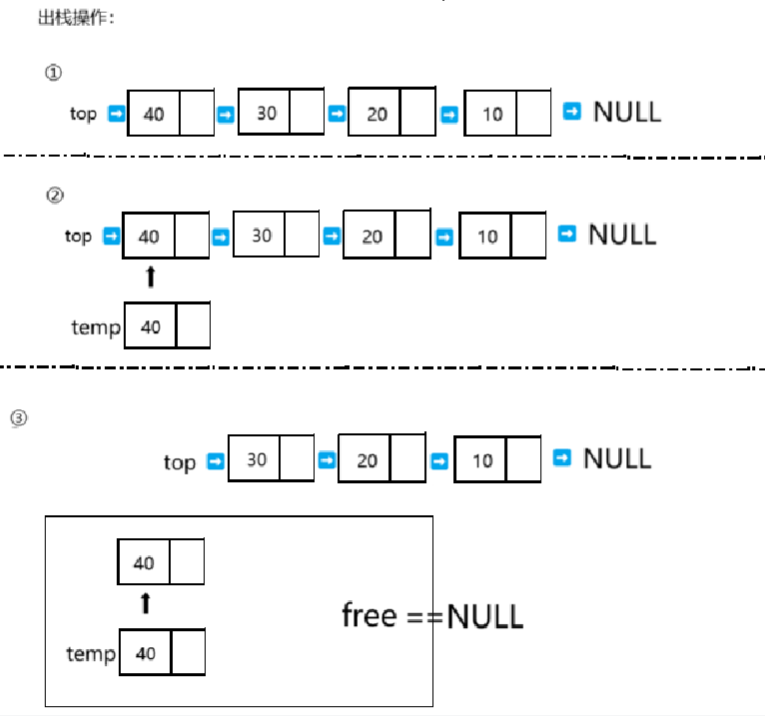
int LStackPop(LinkedStack* S) {
    if (S->top == NULL) return -1;  // 栈空
    
    StackNode* temp = S->top;       // 暂存栈顶
    int elem = temp->data;          // 保存数据
    S->top = S->top->next;          // 栈顶下移
    free(temp);                     // 释放原栈顶
    S->size--;
    return elem;
}

4、获取栈顶元素

 此处指返回，不弹出

int Peek(LinkedStack* S) {
    if (S->top == NULL) return -1;
    return S->top->data;
}

5、判断栈是否为空

int IsEmpty(LinkedStack* S) {
    return S->top == NULL;
}

6、销毁栈（此处理由同顺序栈）

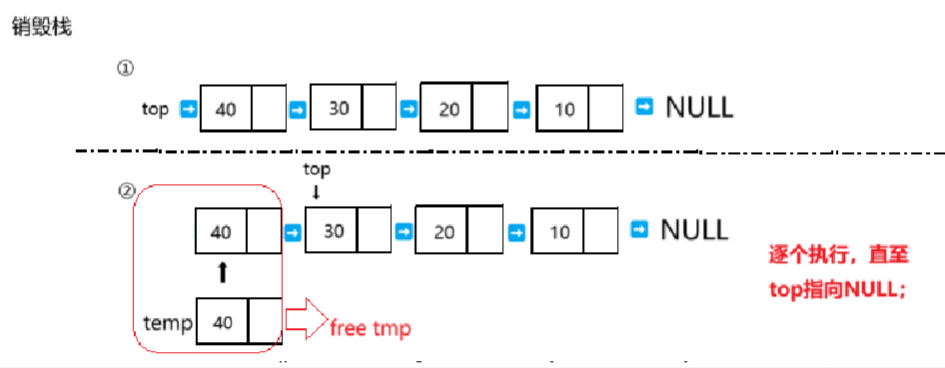
void DestroyStack(LinkedStack* S) {
    while (S->top != NULL) {
        StackNode* temp = S->top;
        S->top = S->top->next;
        free(temp);
    }
    S->size = 0;
}

 主函数测试

#include <stdio.h>
#include <stdlib.h>

int main() {
    // 1. 初始化栈
    LinkedStack stack;
    InitStack(&stack);

    // 2. 入栈测试
    Push(&stack, 10);
    Push(&stack, 20);
    Push(&stack, 30);

    // 3. 查看栈顶
    printf("Top: %d\n", Peek(&stack));

    // 4. 出栈测试
    Pop(&stack);
    printf("After pop, Top: %d\n", Peek(&stack));

    // 5. 判断栈空
    printf("Is empty? %s\n", IsEmpty(&stack) ? "Yes" : "No");

    // 6. 清空栈
    while (!IsEmpty(&stack)) {
        printf("Popping: %d\n", Peek(&stack));
        Pop(&stack);
    }

    // 7. 再次检查栈空
    printf("Is empty now? %s\n", IsEmpty(&stack) ? "Yes" : "No");

    // 8. 销毁栈
    DestroyStack(&stack);

    return 0;
}

 链栈与顺序栈的对比

选择顺序栈还是链栈取决于具体应用场景和对空间、时间的需求

特性	顺序栈	链栈
存储结构	数组（连续内存）	链表（非连续内存）
空间大小	固定	动态扩展
内存利用率	可能有浪费	按需分配
栈满情况	可能发生	除非内存耗尽，否则不会
操作复杂度	O(1)	O(1)
实现难度	简单	较复杂
适用场景	栈大小可预估、频繁存取	栈大小不可预估、需要动态变化