卷积神经网络详解

最新推荐文章于 2025-04-19 17:05:47 发布

ShiningLeeJ

最新推荐文章于 2025-04-19 17:05:47 发布

阅读量1.7k

点赞数 2

分类专栏：深度学习-初级文章标签： cnn 深度学习算法

本文链接：https://blog.youkuaiyun.com/ShiningLeeJ/article/details/126827739

版权

深度学习-初级专栏收录该内容

5 篇文章

订阅专栏

在学习卷积神经网络之前，学习了全连接神经网络，但是全连接神经网络存在一些缺点，并不足以完成大多数深度学习的项目。为了克服这些缺点，学习卷积神经网络。

全连接神经网络缺点

（1）首先将图像展开为向量会丢失空间信息；

（2）其次参数过多效率低下，训练困难；

4 Layer(784, 256, 256, 256, 20) 总共有336896个参数，而这仅仅算是一个多层感知机的结构，还达不到深度神经网络的地步。

在边缘计算场景之中，使用的边缘计算盒子往往没有我们在训练时使用的计算机性能好，导致效率低下。

（3）同时大量的参数也很快会导致网络过拟合。

模型在训练时过于追求把损失降到最低，当此模型测试时，损失反而变高。说明该模型泛化能力差，不能适应训练集以外的其他数据。

举个例子：

现在训练一个模型来识别狗狗，训练的数据恰好全是哈士奇的图片，结果多次迭代后把哈士奇的全部特点都识别成狗狗特有的。这样如果我去识别一只金毛的时候则无法识别。这就是过拟合。

解决办法：

1、训练集增加更多的数据（数据增强）

2、降低模型的复杂度

卷积神经网络缺点

卷积结构可以有效的减少深层神经网络所占用的内存量，有效的减少参数的个数，缓解模型的过拟合问题。主要是通过以下三个操作加以实现：

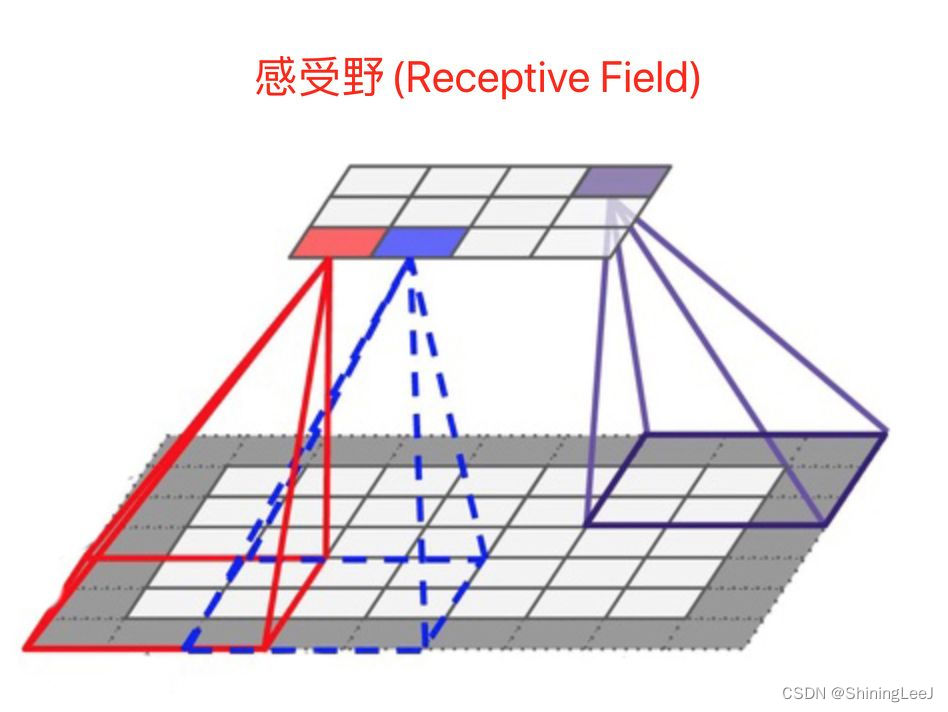
局部感受野

在卷积神经网络中,感受野是指特征图上的某个点能看到的输入图像的区域,即特征图上的点是由输入图像中感受野大小区域的计算得到的。

神经元感受野的值越大表示其能接触到的原始图像范围就越大，也意味着它可能蕴含更为全局，语义层次更高的特征；相反，值越小则表示其所包含的特征越趋向局部和细节。因此感受野的值可以用来大致判断每一层的抽象层次。

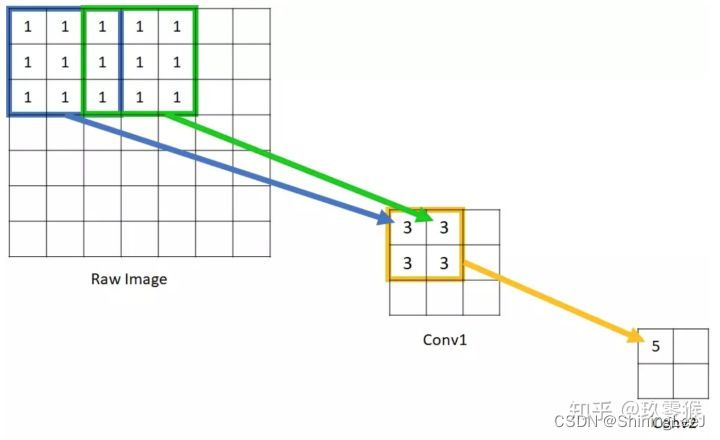
权值共享

给一张输入图片，用一个卷积核去扫描这张图，卷积核里面的数就叫权重，这张图每个位置是被同样的卷积核扫的，所以权重是一样的，也就是共享。其实就是一张图片使用同一个卷积核内的参数。

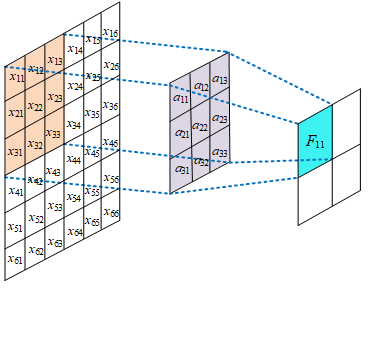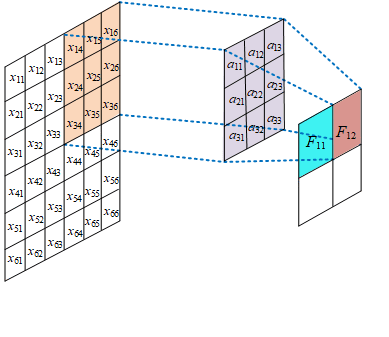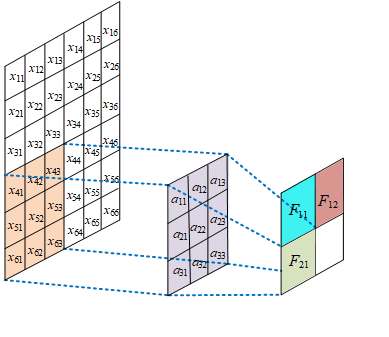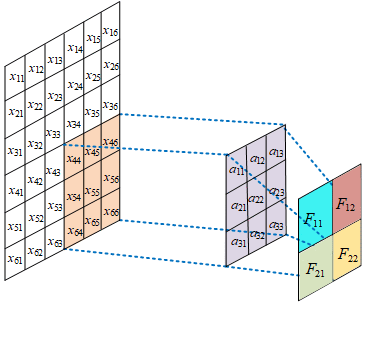
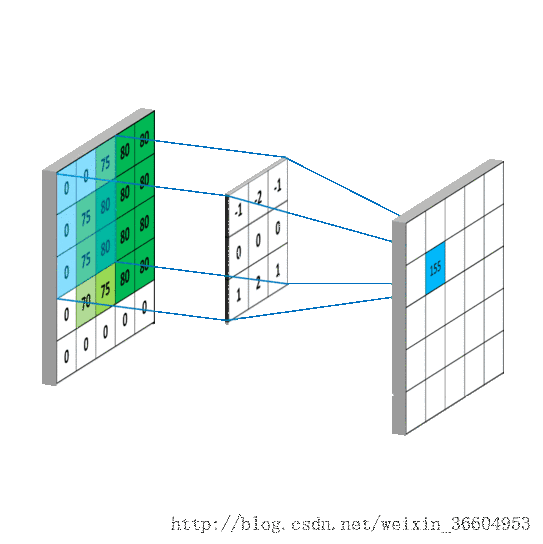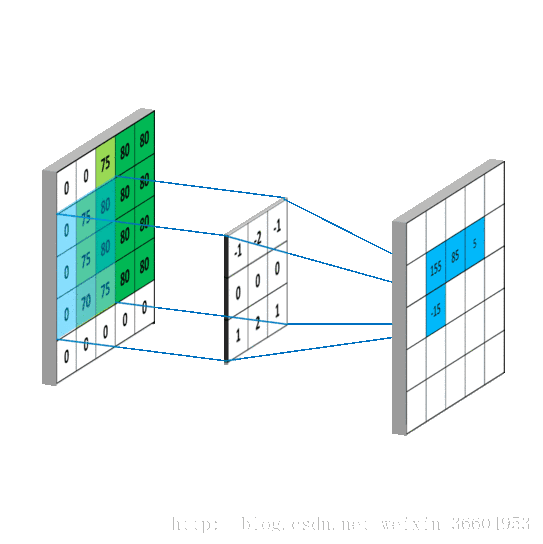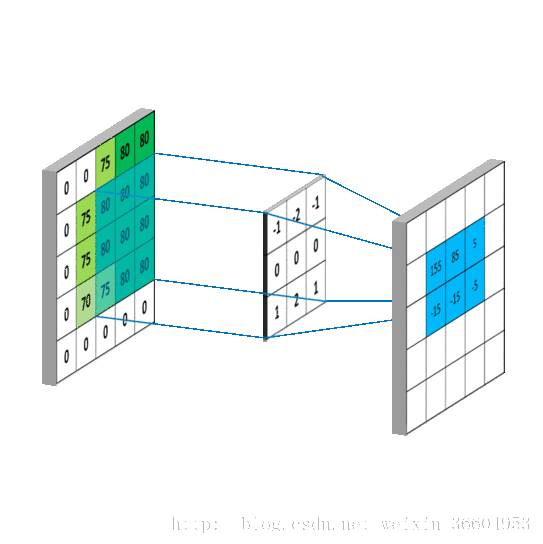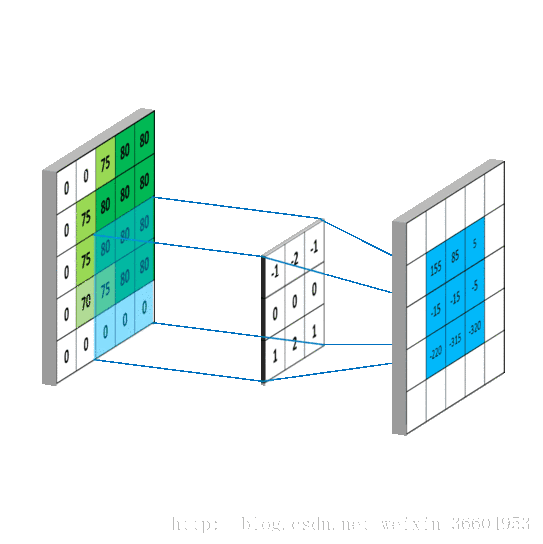
池化层

池化的本质是下采样：压缩数据和参数的数量。

1、特征不变形：池化操作使模型更加关注是否存在某些特征，而不是特征的具体位置。

2、特征降维：在空间范围内做了维度约减，从而使模型可以抽取更加广泛的特征，也减小了下一层的输入大小，减少参数量。

3、防止过拟合，方便优化。对于这点，如上面过拟合所描述的，模型学到了太多不应该去学到的东西，而池化层将这些不应该学习的东西给减少掉。

1.最大池化一般用在网络的浅层

2、平均池化用在浅层和深层均可，使用较少（因为改变了原始特征，产生了新的特征）。

卷积神经网络与全连接神经网络的对比

参数量：

卷积神经网络是权值共享，参数较少；（卷积的参数主要是需要控制通道数）

全连接的参数（W）是由输入数据决定的，参数非常冗余（仅参数就可占整个网络参数80%左右）。

全连接的W多，卷积的W少。

通道：

全连接神经网络是NV结构，没有通道（C）；

卷积神经网络通道（C）会逐渐增多，HW会逐渐减小（数据在减小），所以每一层卷积核的卷积核会增加（把失去的数据补充回来，在C上体现）。

在卷积神经网络中也会专门的针对通道进行优化。

全连接的通道少（无），卷积的通道多

卷积原理

卷积核

卷积核中的数字也就是卷积神经网络之中的权重。对于卷积核来说，它的尺寸大小需要等于或小于图片的尺寸。

卷积核从图像最始端，从左往右、从上往下，以指定步长的间距依次滑过图像的每一个区域。然后再求和，将结果保存到输出的对应位置。

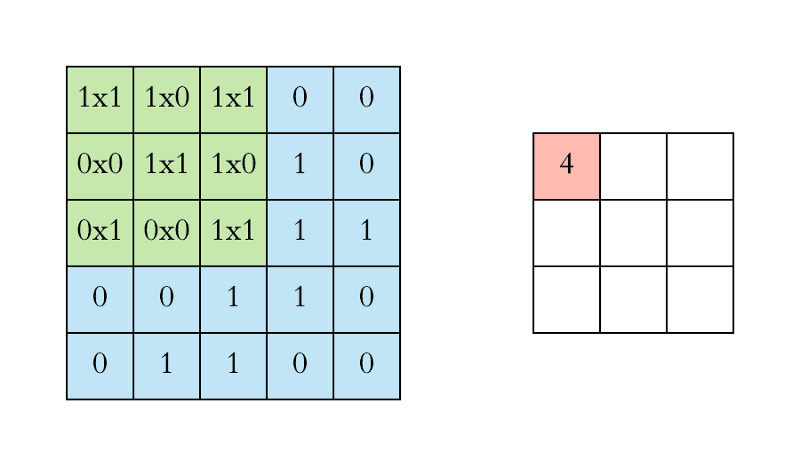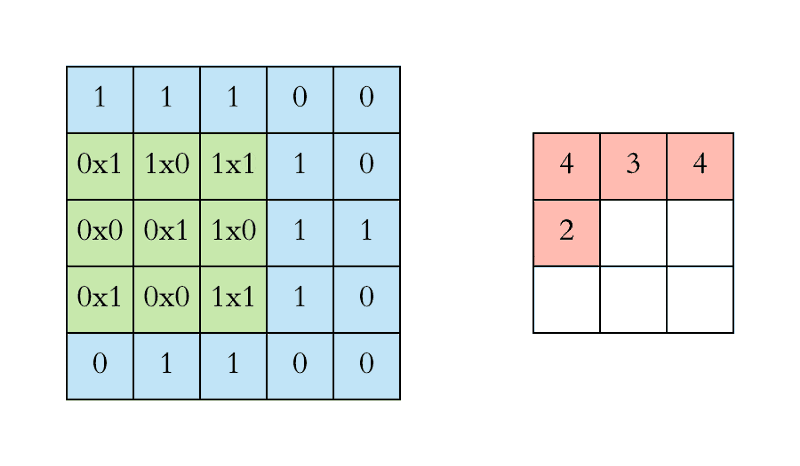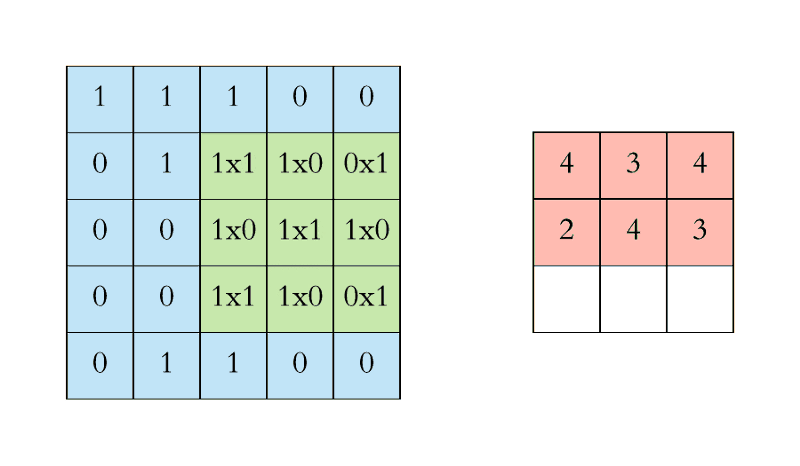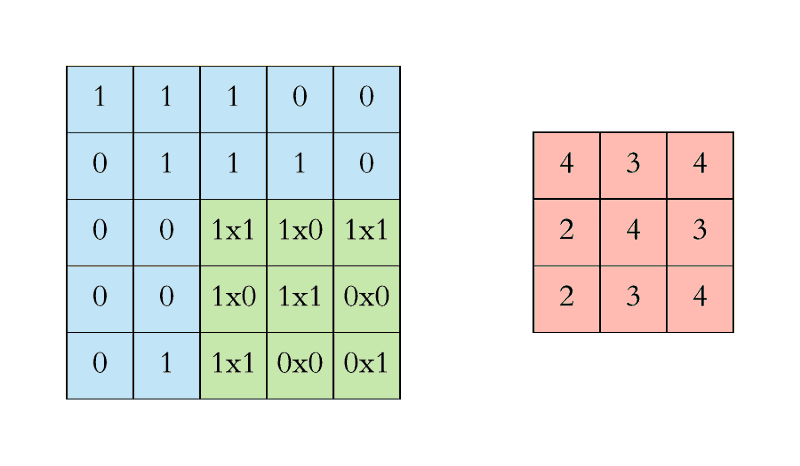
卷积运算

输入的图片是3通道，1个卷积核进行卷积运算：

1、该卷积核是三个通道

2、特征图是一个通道

3、卷积核的输入结构是NCHW

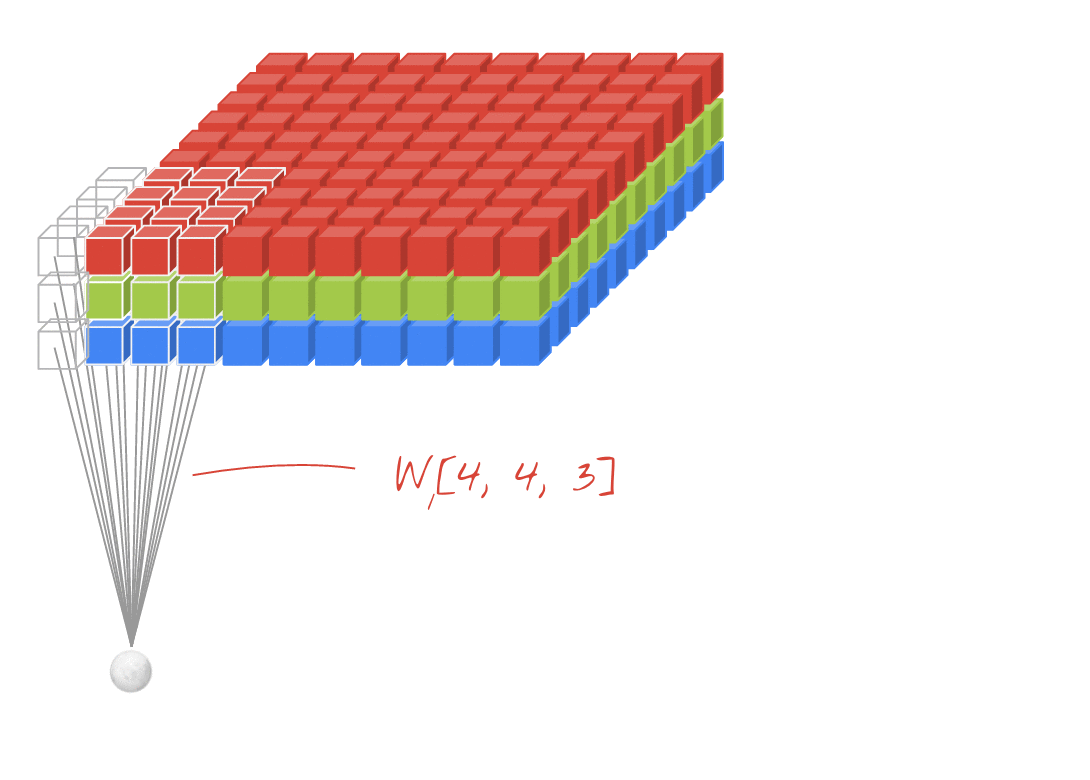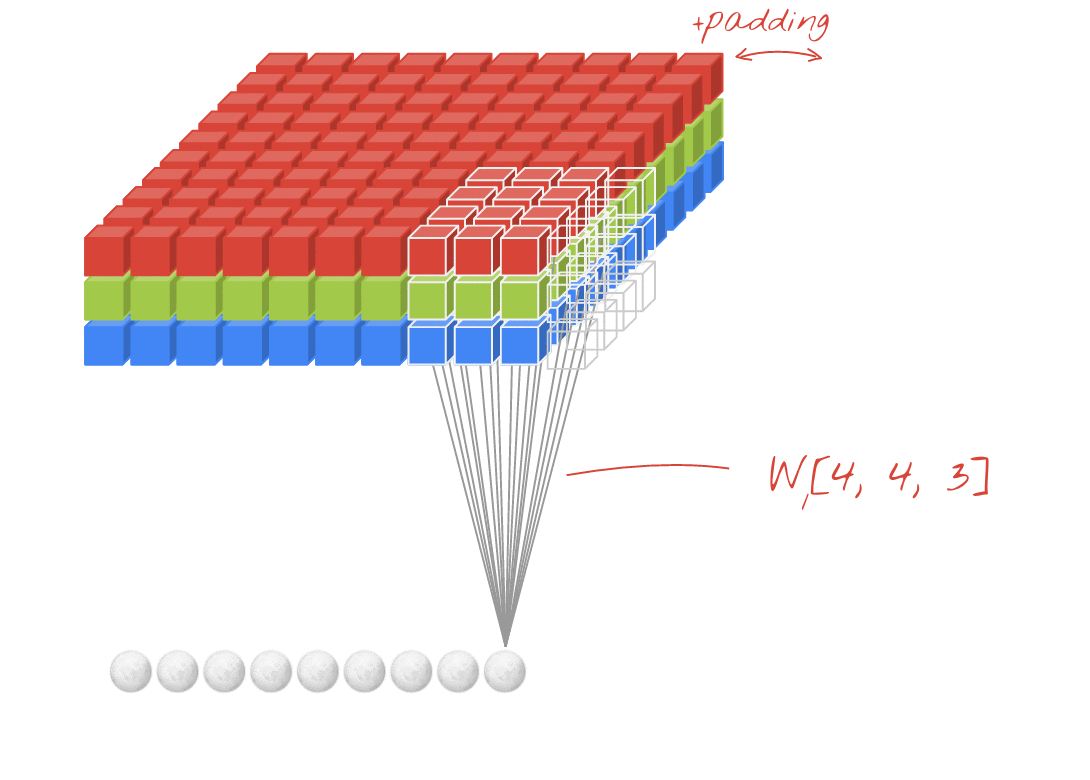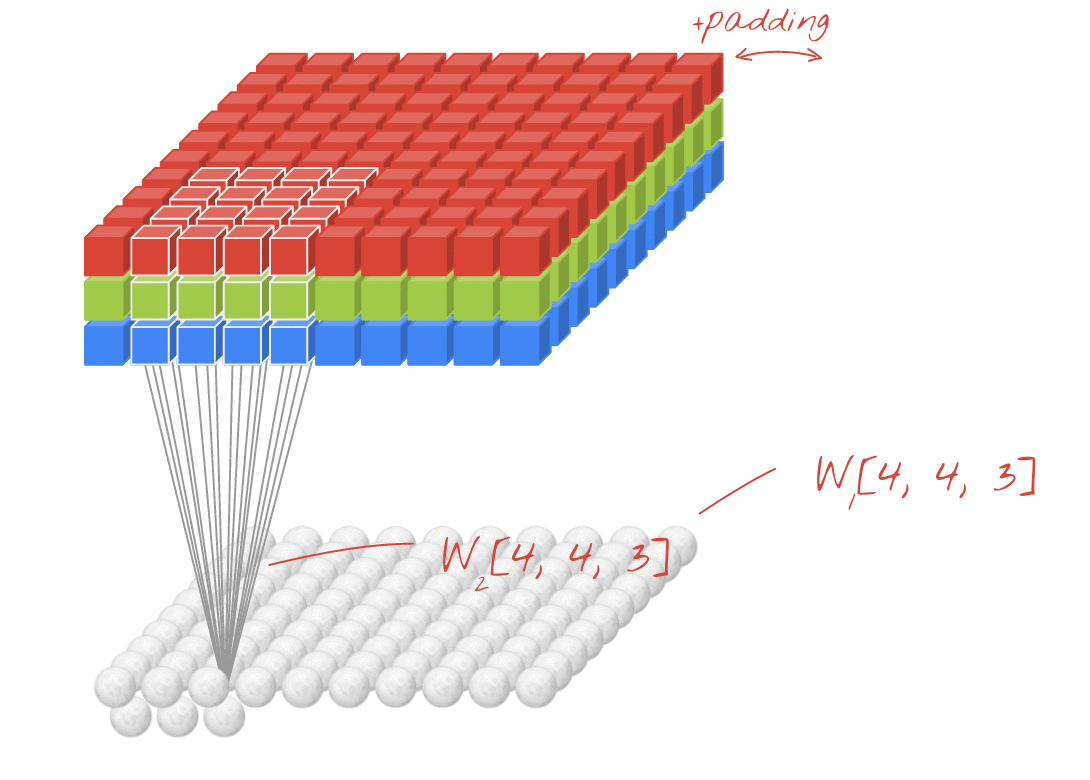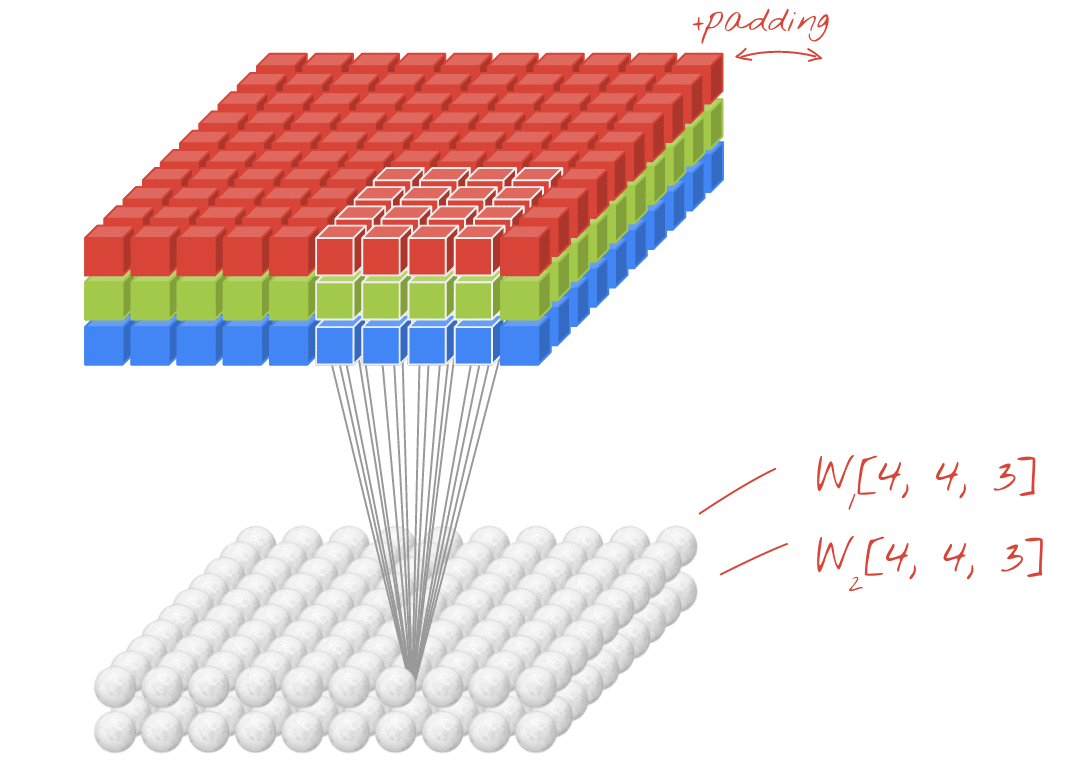
补充：padding填充

卷积神经网络结构分析

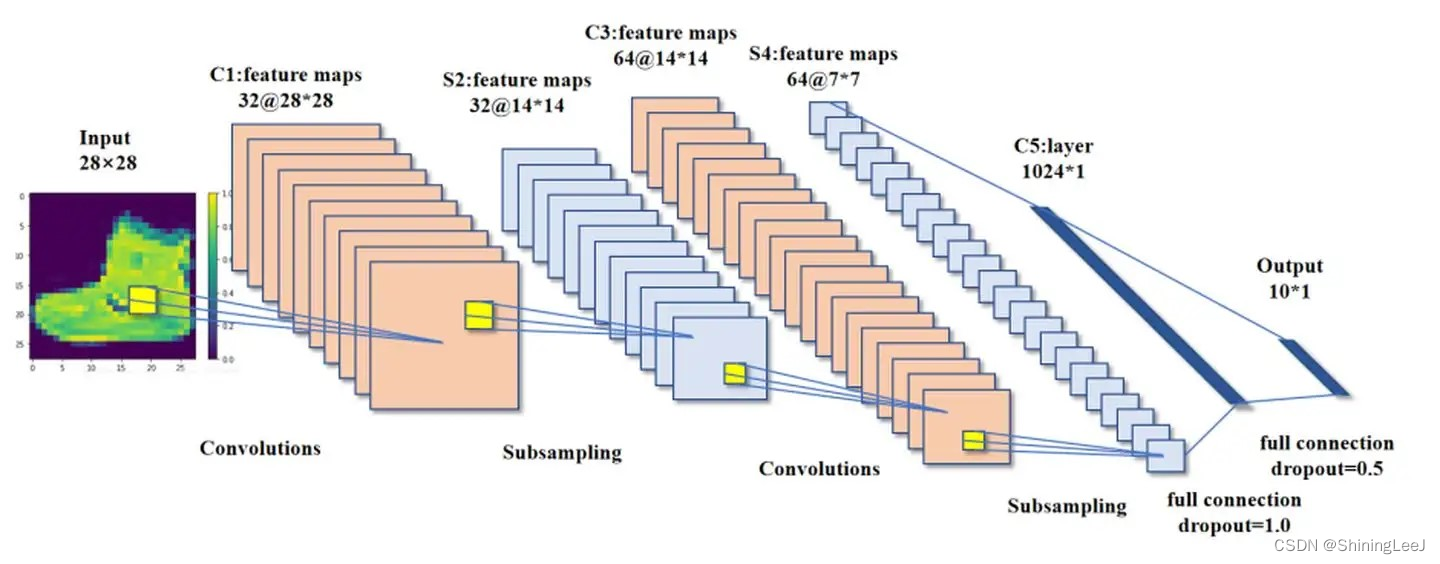
对于上图，图片的C=1,H=28,W=28，在构建卷积神经网络时的输入通道应该为1。经过10个卷积核的运算之后特征图变为C=10,H=26,W=26。

PyTorch实现卷积层：

# 输入通道、输出通道（卷积核的个数）、核的形状、步长
layer = nn.Conv2d(1, 10, 3, 1)

如果图片的通道数变为3，跟上面通道数为1的图片相同。上面的卷积核输入通道为1，而下面的卷积核的输入通道应该变为3。图片经过一个卷积核进行运算时，无论卷积核有多少个通道数，最后生成的特征图也只有一个通道，经过10个卷积核运算之后图像变为C=10,H=26,W=26。

# 输入通道、输出通道（卷积核的个数）、核的形状、步长
layer = nn.Conv2d(3, 10, 3, 1)

残差与batchnormal

在分析反向传播梯度下降的过程中，可能会出现梯度消失或者梯度爆炸的问题。残差是为了解决梯度消失的问题。虽然残差也能延缓梯度爆炸的问题，但是并不能解决梯度爆炸问题，而batchnormal就是专门解决这一问题的方法。

先来复习一下链式法则。在真正的神经网络之中是远远不止的。上一层的输出会带入到下一层的输入，所以就需要运用到链式法则来进行求导。

这里的每一层都使用sigmoid函数进行激活，每一层的输出如下：

对w3的偏导数：

对w2的偏导数：

对w1的偏导数：

梯度消失

梯度消失问题就是在反向传播的时候，对参数链式求导，导数连乘过程中，有一个参数接近于0，则梯度消失了。

如上图进行的推导过程，对于L3和（1-L3），对照sigmoid函数：如果L3的值接近于1，那么（1-L3）会趋近于0，这两个数始终是相对应的，这就会导致梯度消失的问题。这种问题可能在神经网络的前几层并不会出现，但是随着神经网络的加深，梯度消失问题必然会发生。

梯度爆炸

梯度消失问题就是在反向传播的时候，对参数链式求导，导数连乘过程中，参数大于1，则会出现梯度爆炸问题。其推导的过程如上面的梯度消失的推导过程一样。

残差

其实就是在输出的时候加上一个输入参数，把连乘变为连加问题。

对于上图所表示的网络，最后的输出为：

$(((x * w1 + x) * w2 + (x * w1 + x))) * w3 + ((x * w1 + x) * w2 + (x * w1 + x))$

而对上面的结果进行求导时，遵循下图的规则：

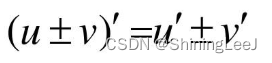
与之前进行的反向求导梯度下降的推导来看，残差网络将求导后连乘的结构转化为了连加的结构，以此来解决梯度消失的问题。

batchnormal

在介绍batchnormal之前，先复习一下最简单的归一化。

而batchnormal也是一种归一化的处理，只是不再像上图所表示的那么简单。

对输入的批数据进行归一化，映射到均值为 0 ，方差为 1 的正态分布。同时因为将输入数据都映射到了原点周围，会导致激活函数表达能力变差，所以又引入了缩放和平移，计算公式如下：

计算过程如下：

首先，计算一个批次之内的均值 μB 和方差 σ2B ，再通过batchnormal的计算公式对输出进行批归一化。

这里需要注意两点：

1.在batchnormal的前一层神经网络中需要将bias置为0。

2.batchnormal通常不i在网络的最后几层中进行使用，因为最后几层的数据量可能比较少，会导致均值和方差不准确。

class Res_Net(nn.Module):
    def __init__(self,c_in,c_out,c):
        super(Res_Net, self).__init__()
        self.layer = nn.Sequential(
            nn.Conv2d(c_in,c,3,1,padding=1,bias=True),
            #nn.BatchNorm2d(c),
            nn.ReLU(),
            nn.Conv2d(c,c_out,3,1,padding=1,bias=True),
            #nn.BatchNorm2d(c_out),
            nn.ReLU()
        )

    def forward(self,x):
        return self.layer(x) + x

信息瓶颈

在讨论信息瓶颈前，需要了解卷积神经网络所存在的缺点。虽然卷积神经网络在很大程度上的减少了参数w和b的数量，但是在通道数量上，卷积神经网络又会导致参数增多。并且甚至会导致卷积神经网络与全连接神经网络相比，运行速度相差不多的情况。

而信息瓶颈可以解决这一问题。信息瓶颈丢弃了一些通道（在CNN进行像素融合时丢掉的，特征就只剩下一部分了，效果类似于最大池化的去噪效果。）

不要过于的担心会丢掉特征，在丢弃特征的同时，也在丢掉噪声。

通道优化

分离卷积

分离卷积从简单的来说，其实就是将卷积核拆分为更小的两个卷积核。再拆分完成之前，完成一次卷积需要计算9次。

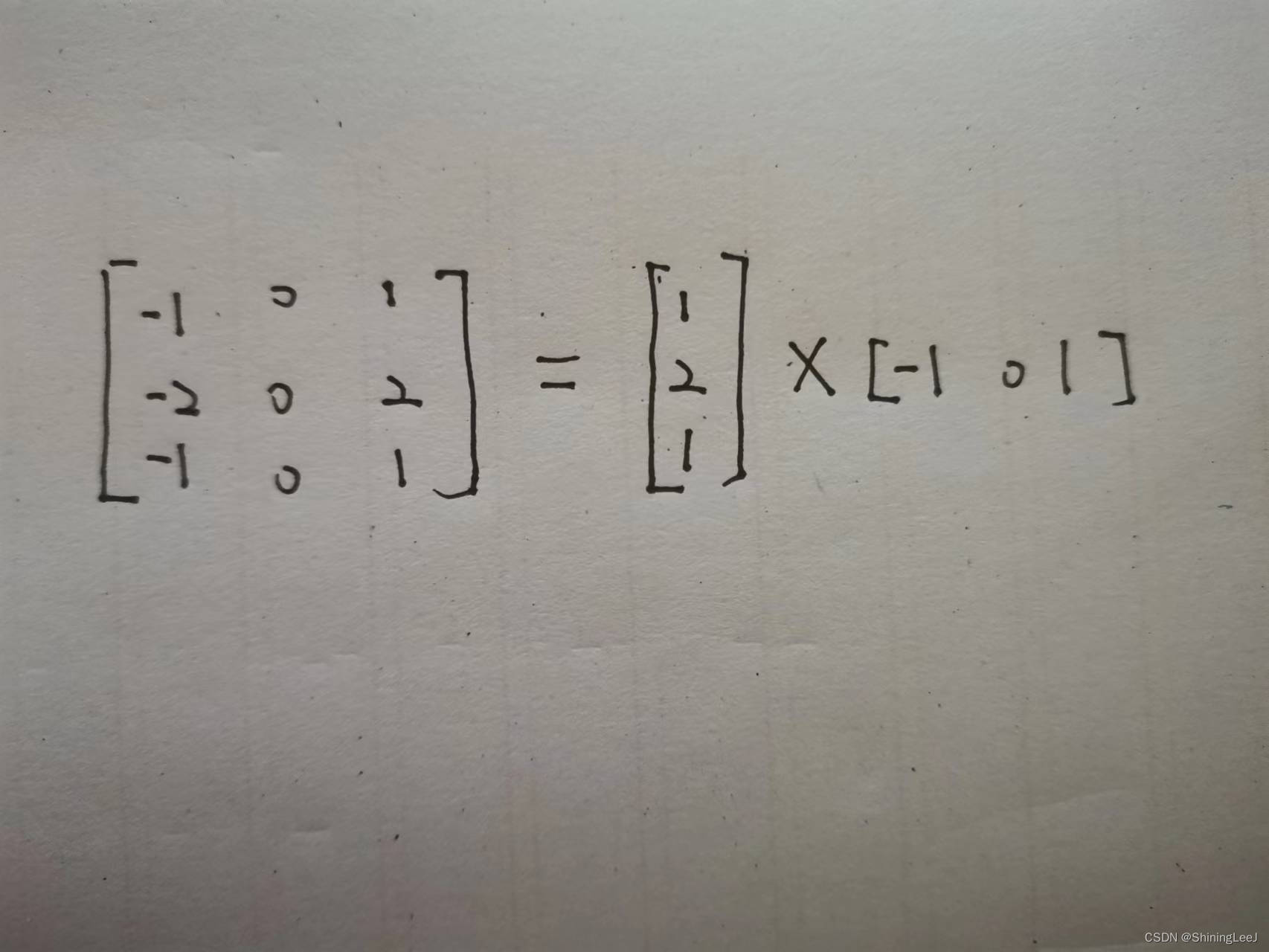
而在进行了上图所示的拆分过后，完成一次卷积只需要计算六次。这样就达到了减少运算量的过程。

但是并不是所有的卷积核都可以拆分为两个小的卷积核，所以出现了深度可分离卷积。下面来看一个普通的卷积：

一张三通道的图片，经过四个卷积核，最后变成了四通道。假设图片的尺寸为12*12，这里可以计算出运算量为：

$10*10*3*3*3*4=10800$

这里看到的运算量好像并不是很大，但是如果卷积核的个数变成512，这个运算量就会陡然增加。

对于深度可分离卷积，将分为两步去分析。首先通过三个3*3的单通道卷积核对图像进行卷积，得到三张特征图。

然后再使用1*1的三通道卷积核对三张特征图进行卷积，的到最后的结果。

通过上面两步的卷积，运算量为：

$10*10*3*3*3+10*10*3*4=3900$

大大的减少了运算量。

import torch.nn as nn

layer1 = nn.Conv2d(6, 6, 3, 1, groups=1)
layer2 = nn.Conv2d(6, 6, 3, 1, groups=2)
layer3 = nn.Conv2d(6, 6, 3, 1, groups=3)
layer4 = nn.Conv2d(6, 6, 3, 1, groups=6)  # 深度可分离卷积

通道混洗

一个次卷积之后，能够像（b）一样将特征图之间的通道信息进行融合，将每一个组的特征分散到不同的组之后，再进行下一个组卷积。这样输出的特征就能够包含每一个组的特征，而如图（c）所示，通道混洗恰好可以实现这个过程。

import torch

x = torch.randn(1, 6, 1, 1)
print(x)
x = x.reshape(1, 2, 3, 1, 1)
x = torch.permute(x, (0, 2, 1, 3, 4))
print(x)