数学：反向传播算法(BP 算法)

最新推荐文章于 2024-07-02 20:59:51 发布

ShellDawn

最新推荐文章于 2024-07-02 20:59:51 发布

阅读量332

点赞数 1

CC 4.0 BY-SA版权

文章标签： BP算法反向传播算法

本文链接：https://blog.youkuaiyun.com/ShellDawn/article/details/87969773

本文详细解析了神经网络的前向与反向传播过程，包括权重更新的数学原理，如sigmoid函数及其导数的计算，均方误差的定义，以及如何通过反向传播调整权重以最小化损失。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

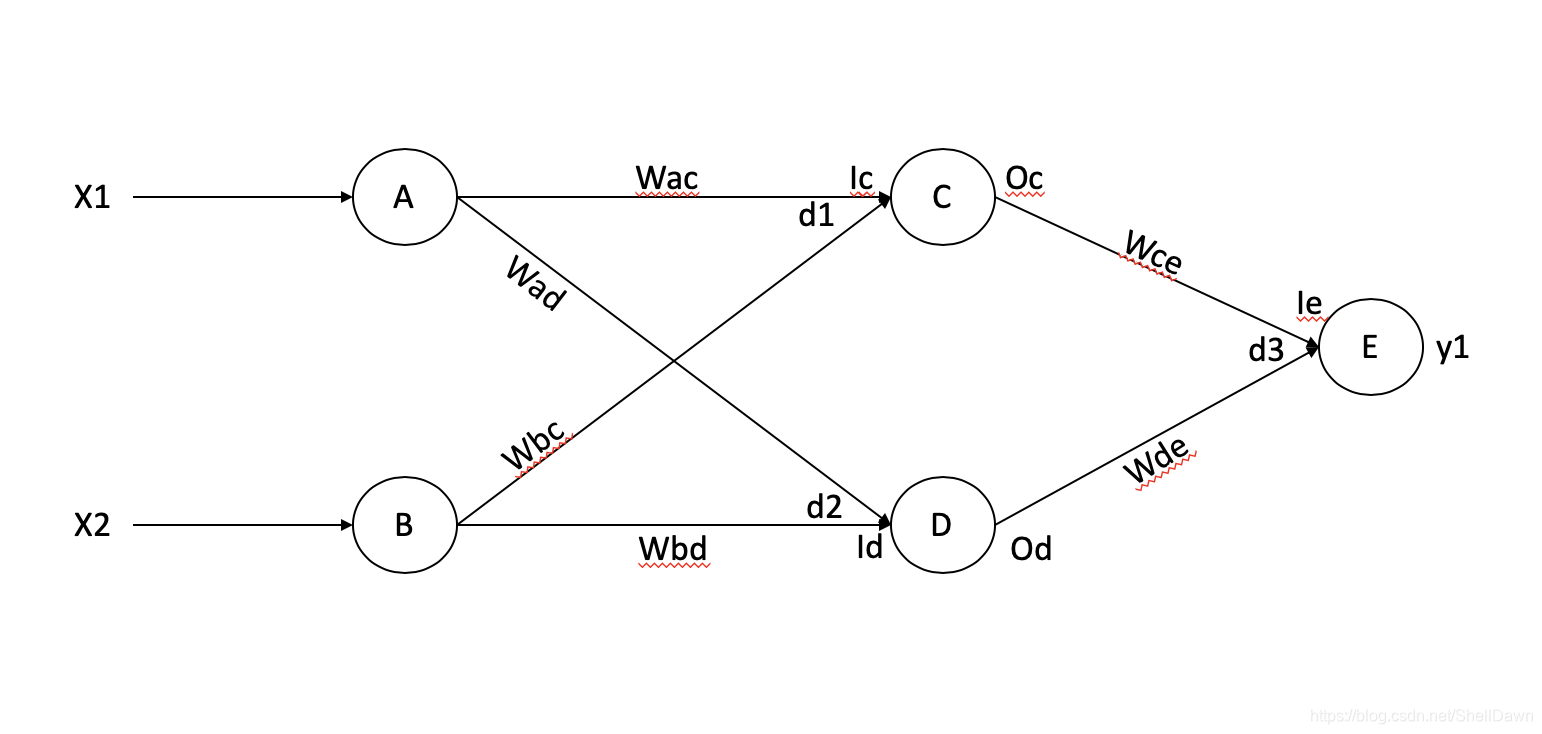
ShellDawn反向传播图
前向传播：
此时，X1, X2, Wac, Wad, Wbc, Wbd, d1, d2, Wce, Wde, d3都是已知量。
Ic = Wac * X1 + Wbc * X2 + d1
Id = Wad * X1 + Wbd * X2 + d2
Oc = sigmoid(Ic)
Od = sigmoid(Id)
Ie = Wce * Oc + Wde * Od + d3
y1 = sigmoid(le)

均方误差：
J = 1/2 * (y1 - y)^2

sigmoid导数：
Sigmoid(x)’ = Sigmoid(x) * (1-sigmoid(x))

反向传播：
此时，y, y1, le, Od, Oc, Id, Ic也都是已知量。
D{J} / D{y1} = y1 - y
D{J} / D{le} = D{J} / D{y1} * D{y1} / D{le} = (y1 - y)y1(1 - y1)
D{J} / D{Wce} = D{J} / D{le} * D{le} / D{Wce} = (y1 - y)y1(1 - y1)Oc
D{J} / D{Oc} = D{J} / D{le} * D{le} / D{Wde} = (y1 - y)y1(1 - y1)Wce
D{J} / D{lc} = D{J} / D{Oc} * D{Oc} / D{lc} = (y1 - y)y1(1 - y1)WceOc(1-Oc)
D{J} / D{Wac} = D{J} / D{lc} * D{lc} / D{Wac} = (y1 - y)y1(1 - y1)WceOc(1-Oc)*X1