数据结构与算法之二分查找及场景应用（Java）

目录

1.列表查找

1.1 什么是列表查找

1.2 顺序查找（Linear Search）

1.3 二分查找（折半查找）（Binary Search）

1.4 维度对比

2.二分查找场景应用

2.1 不采用二分查找方法

2.2 采用二分查找方法

2.3 不同维度对比

---

1.列表查找

1.1 什么是列表查找

       查找：在一些数据元素中，通过一定的方法找出与给定关键字相同的数据元素的过程

       列表查找（线性表查找）：从列表中查找指定的元素

• 输入：列表，待查找元素
• 输出：元素下标（未找到元素时一般返回-1）

1.2 顺序查找（Linear Search）

        思想介绍：循环列表，直到找到目标元素，返回目标元素的下标位置，若未找到返回-1

        代码实现：

 public static int linearSearch(int[] linear, int val) {
        for (int i = 0; i < linear.length; i++) {
            if (linear[i] == val) {
                return i;
            }
        }
        return -1;
    }

         测试代码：

  public static void main(String[] args) {
        int[] arr = {7, 9, 6, 3, 5};
        System.out.println("顺序查找6元素的下标是：" + linearSearch(arr,6));
    }

         运行结果：

顺序查找6元素的下标是：2

1.3 二分查找（折半查找）（Binary Search）

        思想介绍： 从有序列表的初始候选区arr[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

        例如从以下列表中查找元素3：

1

2

3

4

5

6

7

8

9

         代码实现：

  public static int binarySearch(int[] arr, int val) {
        int left = 0;
        int right = arr.length - 1;
        int mid = 0;
        while (left <= right) {
            mid = (left + right) / 2;
            if (val == arr[mid]) {
                return mid;
            } else if (val > arr[mid]) {
                left = mid + 1;
            } else if (val < arr[mid]) {
                right = mid - 1;
            }
        }
        return -1;
    }

           测试代码：

public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
        System.out.println("元素3在数组中处于第(" + (binarySearch(arr, 3) + 1) + ")位");
    }

           运行结果：

元素3在数组中处于第(3)位

1.4 维度对比

算法	代码复杂度	时间复杂度	空间复杂度	列表条件
顺序查找方法	简单	o(n)	o(1)	无序列表，有序列表皆可
二分查找方法	较复杂	o(logn)	o(1)	有序列表

2.二分查找场景应用

场景：搜索二维矩阵

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

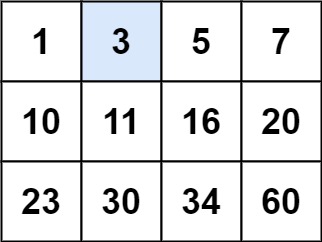
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

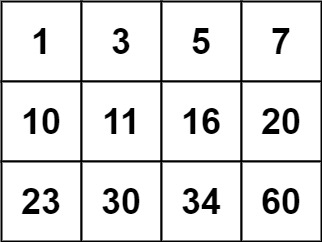
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

​​​​​​​提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

2.1 两层顺序查找方法

代码实现：

 public static boolean searchMatrix(int[][] matrix, int target) {
        for (int[] i : matrix) {
            for (int j : i) {
                if (target == j) {
                    return true;
                }
            }
        }
        return false;
    }

2.2 采用二分查找方法

把二维数组，看成一个有序列表，排列之后的结果是：

1

3

5

7

10

11

16

20

23

30

34

60

无非就是通过每次找到一个中间元素之后，需要计算该元素的行标和列表

height：3

width：4

left：0

right：3*4-1=11

mid: （left+right）/2

跟目标比较的元素的行标和列标：i=mid/width,j=mid%width

代码实现：

public static boolean binarySearchMatrix(int[][] matrix, int target) {
        int height = matrix.length;
        if (height == 0) {
            return false;
        }
        int width = matrix[0].length;
        if (width == 0) {
            return false;
        }
        int left = 0;
        int right = height * width - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            int i = mid / width;
            int j = mid % width;
            if (matrix[i][j] == target) {
                return true;
            } else if (matrix[i][j] > target) {
                right = right - 1;
            } else if (matrix[i][j] < target) {
                left = left + 1;
            }
        }
        return false;
    }

测试用例

测试用例	运行结果
数组： int[][] matrix = new int[][]{{1, 3, 5, 7}, {10, 11, 16, 20}, {23, 30, 34, 60}}; target：13	false
数组： int[][] matrix = new int[][]{{1, 3, 5, 7}, {10, 11, 16, 20}, {23, 30, 34, 60}}; target：16	true
数组: int[][] matrix = new int[][]{{1}} target:1	true

测试代码：

    public static void main(String[] args) {
        int[][] matrix1 = new int[][]{{1}};
        int[][] matrix = new int[][]{{1, 3, 5, 7}, {10, 11, 16, 20}, {23, 30, 34, 60}};
        System.out.println("生成的二位数组是" + Arrays.deepToString(matrix1));
        System.out.println("非二分查找1的结果是" + searchMatrix(matrix1, 1));
        System.out.println("二分查找的1结果是" + binarySearchMatrix(matrix1, 1));
        System.out.println("非二分查找13的结果是" + searchMatrix(matrix, 13));
        System.out.println("二分查找13的结果是" + binarySearchMatrix(matrix, 13));
        System.out.println("非二分查找16的结果是" + searchMatrix(matrix, 16));
        System.out.println("二分查找的16结果是" + binarySearchMatrix(matrix, 16));
    }

运行结果：

生成的二位数组是[[1]]
非二分查找1的结果是true
二分查找的1结果是true
非二分查找13的结果是false
二分查找13的结果是false
非二分查找16的结果是true
二分查找的16结果是true

2.3 维度对比

算法	代码复杂度	时间复杂度	空间复杂度	二维数组条件
两层顺序查找方法	简单	o(m*n)	o(1)	无序数组，有序数组皆可
二分查找方法	较复杂	o(logm*n)	o(1)	有序数组