Moamen and XOR（快速幂、组合数学）

一、题意

给定n和k，代表着有n个数，其中每个数的值都比 小，并且这n个数都满足以下不等式

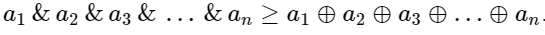
求有多少种符合题意的方案

二、思路

参考文章

注意：最后偶数里面，前面相等的数量和后面随便取的数量，两者是相乘的

三、代码

#include<bits/stdc++.h>
using namespace std;
const int p = 1e9+7;
long long quickpow(long long a, long long b)
{
	long long ret = 1, base = a;
	while(b > 0)
	{
		if(b & 1) ret = ret*base%p;
		base = base*base%p;
		b >>= 1;
	}
	return ret%p;
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		long long n,k,ans;
		scanf("%lld%lld",&n,&k);
		if(k == 0) printf("1\n");
		else if(n & 1)
		{
			ans = quickpow(2, n-1)+1;
			ans = quickpow(ans, k);
			printf("%lld\n",ans%p);
		}
		else
		{
			ans = quickpow(2, n-1)-1;
			ans = quickpow(ans, k);
			for(int i=1; i<=k; ++i)
			{
				long long sum,cnt;
				sum = quickpow(2,n-1)-1;
				sum = quickpow(sum, i-1);
				cnt = quickpow(2, n);
				cnt = quickpow(cnt, k-i);
				ans = (ans+sum*cnt%p)%p;
			}
			printf("%lld\n",ans%p);
		}
	}
	return 0;
}