二叉树 ——（创建与非递归遍历）

二叉树

定义：

二叉树是结点的有限集合，这个集合或者是空的，或者由一个根结点或两棵互不相交的称为左子树的和右子树的二叉树组成。

特点：

1）每个结点至多有二棵子树(即不存在度大于2的结点)

2）二叉树的子树有左、右之分，且其次序不能任意颠倒

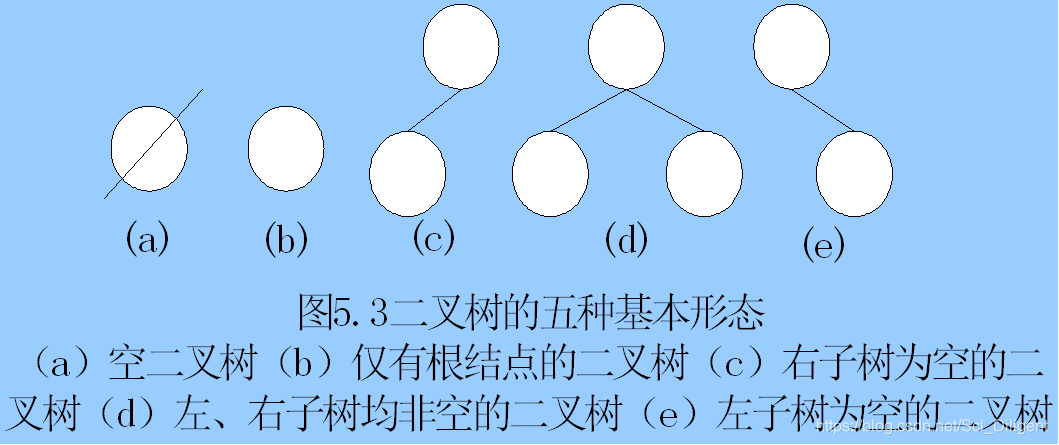
 两种特殊的二叉树：

（1）满二叉树：一棵深度为k且有2k-1个结点的二叉树。

（对树中结点按从上到下、从左到右的顺序进行编号）

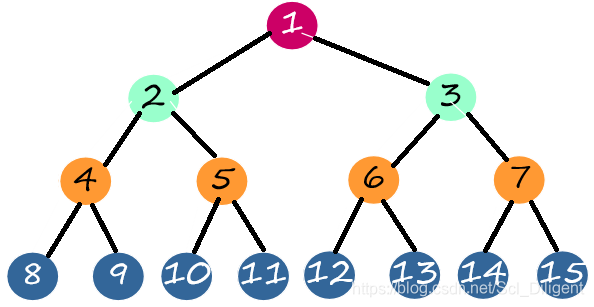
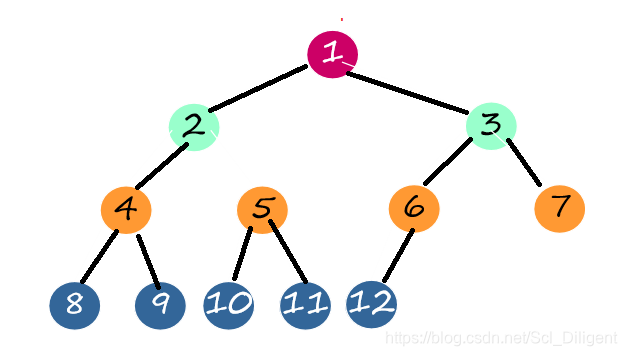
（2）完全二叉树：若二叉树的深度为k，且共有n个结点。对树中结点按从上到下、从左到右的顺序进行编号，若编号为i(1≤i≤n)的结点与满二叉树编号为i的结点位置相同，则此树称为完全二叉树。

（除第k层外，其它各层(1 ~ k-1)的结点数都达到最大个数，第k层从右向左连续缺若干结点，这就是完全二叉树。）\

 

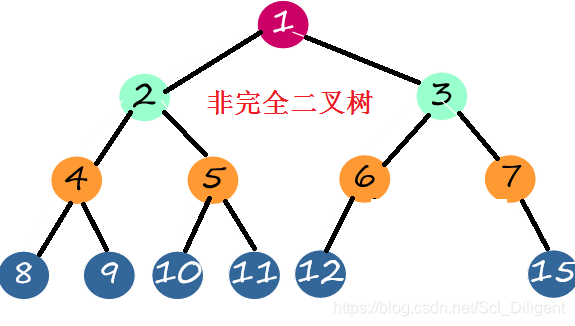
性质：

（1）若二叉树的层次从1开始, 则在二叉树的第 i 层最多有 2i-1 个结点。( i >= 1)。

（2）深度为k的二叉树最多有 2k-1个结点（K >= 1）。

（3）对任何一棵二叉树, 如果其叶结点个数为n0，度为2的结点个数为 n2, 则有n0＝n2＋1。

（4）具有n个结点的完全二叉树的深度为  log2n +1。

（5）对于具有n个结点的完全二叉树，若从上至下和从左至右的顺序对二叉树中的所有结点从1开始编号，则对任意的结点i有:

      a、若i>1,则其双亲为i/2（整除），若i=1,i无双亲结点。

     b、若2i<=n,则i的左孩子序号为2i,若2i>n,则i无左孩子。

     c、若2i+1<=n,则i的右孩子序号为2i+1,若2i+1>n,则i无右孩子。

二叉树的创建：

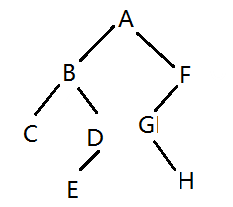
先序遍历（根左右）：ABCDEFGH

中序遍历（左根右）：CBDEAGHF

后序遍历（左右根）：CDEBHGFA

  （1）以先序遍历方式创建二叉树（因为中序和后序节点跳动太大且没有联系）：

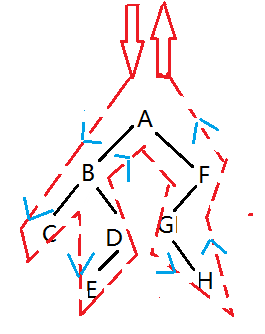
（空节点记为“#”，ABC##DE###FG#H###）

BtNode * CreateTree1() //先序
{
	BtNode * s = NULL;
	ElemType item;
	cin>>item;
	if(item != '#')
	{
		s = BuyNode ();
		s->leftchild = CreateTree1();
		s->data = item;
		s->rightchild = CreateTree1();
	}
	return s;
}

BtNode *CreateTree2(ElemType *&str)  //
{
	BtNode * s = NULL;
	if(*str != '#' && str != NULL)
	{
		s = BuyNode();
		s->data = *str;
		s->leftchild = CreateTree2 (++str);
		s->rightchild = CreateTree2 (++str);
	}
	return s;
}

void CreateTree3(BtNode *&p, ElemType *&str)
{
	if(str == NULL || *str == '#')
	{
		p = NULL;
	}
	else
	{
		p = BuyNode();
		p->data = *str;
       CreateTree3 (p->leftchild , ++str);
	   CreateTree3(p->rightchild, ++str);
	}
}

（2）由遍历序列创建二叉树

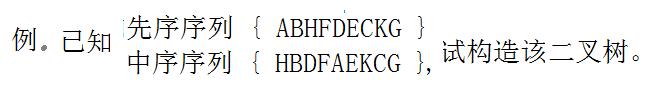
从先序序列开始，取根（A），在中序序列中以根（A）为界限分为左子树集和右子树集。再回到先序序列取根（B），中序序列列划分左右子树，直到先序序列取完。

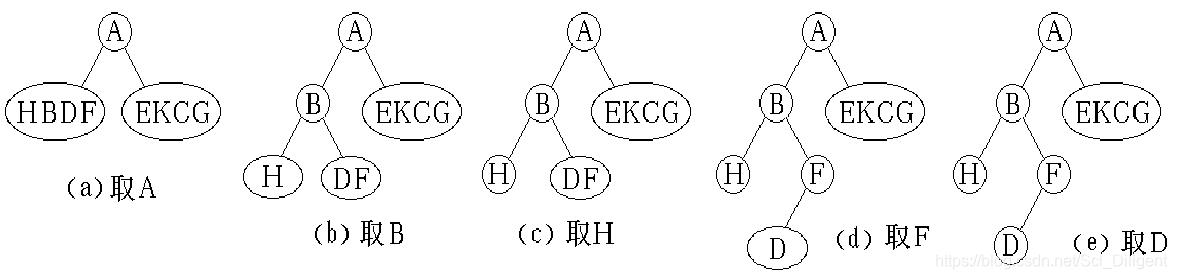
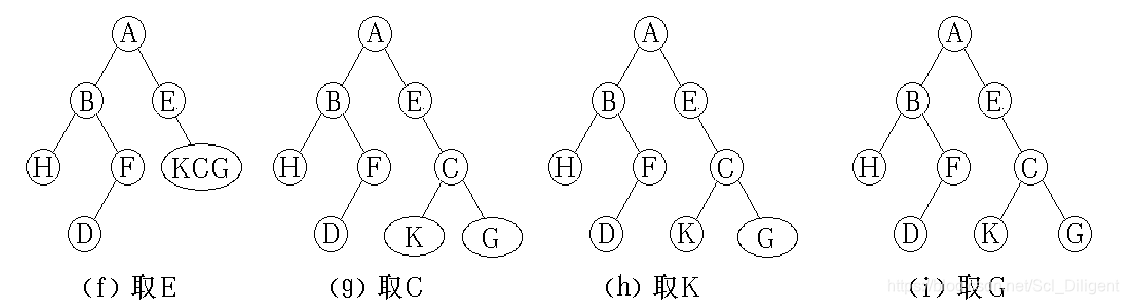
若给出先序和中序可以唯一地确定一棵二叉树，给出中序和后序也可以唯一地确定一棵二叉树,    但给出先序和后序不能唯一地确定一棵二叉树。

（注意：如先序为A、B，后序为B、A,则可得到两 棵不同的二叉树（如下图））

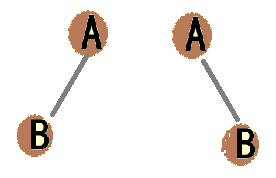
BtNode* CreateTreePreIn(ElemType * ps, ElemType *is, int n)	//先序、中序
{
	BtNode* s = NULL;
	if(n>0)
	{
		s = BuyNode();
		s->data = ps[0];
		int pos = FindPos(is, ps[0], n ); 
		if(pos == -1) 
			exit(0);
		s->leftchild = CreateTreePreIn(ps+1, is, pos);
		s->rightchild = CreateTreePreIn(ps+pos+1, is+pos+1, n-pos-1 );
	}
	return s;
}
BtNode* CreateTreeIL( ElemType *is,ElemType * ls, int n) //中序、后序
{
	BtNode* s = NULL;
	if(n>0)
	{
		s = BuyNode();
		s->data = ls[n-1];
		int pos = FindPos(is, ls[n-1], n ); 
		if(pos == -1) 
			exit(0);
		s->leftchild = CreateTreeIL(is, ls, pos);
		s->rightchild = CreateTreeIL(is+pos+1, ls+pos, n-pos-1 );
	}
	return s;
}

（3）以数组创建二叉树

对于具有n个结点的完全二叉树，若从上至下和从左至右的顺序对二叉树中的所有结点从1开始编号，则对任意的结点i有:

      a、若i>1,则其双亲为i/2（整除），若i=1,i无双亲结点。

     b、若2i<=n,则i的左孩子序号为2i,若2i>n,则i无左孩子。

     c、若2i+1<=n,则i的右孩子序号为2i+1,若2i+1>n,则i无右孩子。

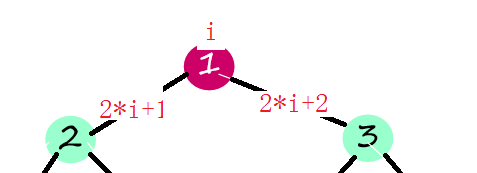
BtNode* CreateTreeAr(ElemType * ar, int i, int n)
{
	BtNode* s = NULL;
	if(NULL != ar && i < n)
	{
		s = BuyNode();
		s->data = ar[i];
		s->leftchild = CreateTreeAr (ar, 2*i+1, n);
		s->rightchild = CreateTreeAr(ar, 2*i+2, n);
	}
	return s;
}

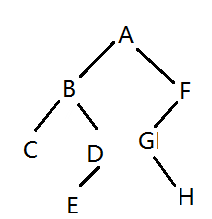
二叉树的查询：

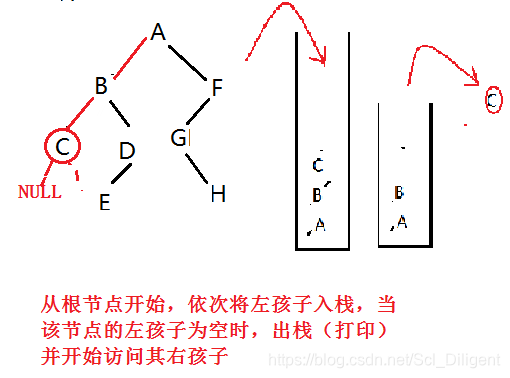
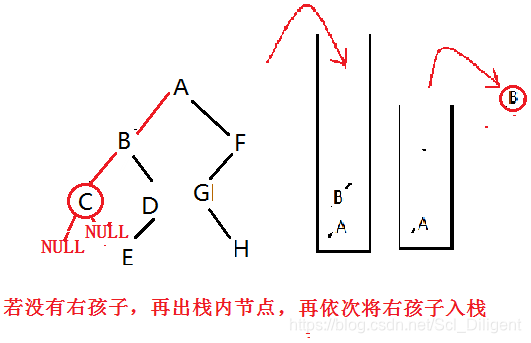
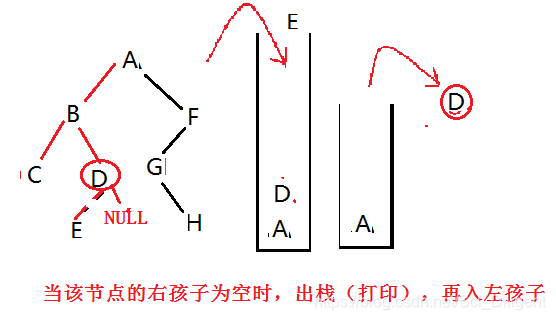
非递归中序遍历二叉树：

（1）从根节点开始，依次将左孩子入栈，当该节点的左孩子为空时，出栈（打印）并开始访问其右孩子；

（2）再依次将右孩子入栈（若没有右孩子，再出栈内节点，重复（2）直到栈空退出），当该节点的右孩子为空时，出栈（打印），回到（1）。

void NiceInOrder(BtNode * ptr)
{
	if(NULL == ptr)
		return;
	stack<BtNode *>st;
	while(ptr != NULL || !st.empty())
	{
		while(ptr != NULL)
		{
			st.push(ptr);
			ptr = ptr->leftchild ;
		}
		ptr = st.top();
		st.pop();
		cout<< ptr->data <<" ";
		ptr = ptr->rightchild ;
	}
	cout<<endl;
}

非递归先序遍历：

（1）先将节点入栈。

（2）节点出栈，其右孩子（存在）入栈，其左孩子（存在）入栈。

（3）重复（2）直到栈空。 

void NicePreOrder(BtNode *ptr)
{
	if(NULL == ptr) return ;
	stack<BtNode *> st;
	st.push(ptr);
	while(!st.empty())
	{
		ptr = st.top(); st.pop();
		cout<<ptr->data<<" ";
		if(ptr->rightchild != NULL)
		{
			st.push(ptr->rightchild);
		}
		if(ptr->leftchild != NULL)
		{
			st.push(ptr->leftchild);
		}
	}
	cout<<endl;
}

非递归后序遍历：

因为后序遍历是“左右根”的顺序，所以根节点是最后访问的。为了确保“根”的左右孩子已经（打印），所以给每一个节点增填一个标记，初始化为0，每出一次栈+1,。标记为1时左孩子还没访问，所以再将该节点和其入栈左孩子（存在）。标记为2时右孩子还没访问（左孩子已经访问），所以再将该节点和其入栈右孩子。标记为3时，打印该节点数据。

struct StkNode
{
	BtNode *pnode;
	int popnum; 

	StkNode(BtNode *p = NULL):pnode(p),popnum(0) {}  //标记初始化为0
};
void StkNicePastOrder(BtNode *ptr)	//非递归后序遍历
{
	if(NULL == ptr) return ;
	stack<StkNode> st;
	st.push(StkNode(ptr));
	while(!st.empty())
	{
		StkNode node = st.top(); st.pop(); 
		if(++node.popnum == 3)			//每次出栈+1，为3时打印
		{
			cout<<node.pnode->data<<" ";
		}
		else
		{
			st.push(node);  //该节点还有左右孩子没访问，所以继续入栈
			if(node.popnum == 1 && node.pnode->leftchild != NULL)  //标记为1时左孩子还没访问
			{
				st.push(StkNode(node.pnode->leftchild));
			}else if(node.popnum == 2 && node.pnode->rightchild != NULL)  //标记为2时右孩子还没访问（左孩子已经访问）
			{
				st.push(StkNode(node.pnode->rightchild));
			}
		}
	}
	cout<<endl;
}

void StkNiceInOrder(BtNode *ptr)   //非递归中序遍历
{
	if(NULL == ptr) return ;
	stack<StkNode> st;
	st.push(StkNode(ptr));
	while(!st.empty())
	{
		StkNode node = st.top(); st.pop();
		if(++node.popnum == 2)  
		{
			cout<<node.pnode->data<<" ";
			if(node.pnode->rightchild != NULL)
			{
				st.push(StkNode(node.pnode->rightchild));
			}
		}
		else
		{
			st.push(node);
			if(node.popnum == 1 && node.pnode->leftchild != NULL)
			{
				st.push(StkNode(node.pnode->leftchild));
			}
		}
	}
	cout<<endl;
}

判断是否是满二叉树：

（一棵深度为k且有2k-1个结点的二叉树）

bool Is_Full_BinaryTree(BtNode *ptr)
{
	bool res = true;
	if( ptr == NULL)
		return res;
	queue<BtNode*> qu;
	int n = 1;
	qu.push (ptr);
	while(!qu.empty() )
	{
		int i = 0;
		for(; i < n && !qu.empty() ; ++i)
		{
			ptr = qu.front(); 
			qu.pop();  //出一次入两次
			if(ptr->leftchild  != NULL)
				qu.push(ptr -> leftchild);
			if(ptr->rightchild != NULL)
				qu.push(ptr->rightchild );
		}
		//不相等则不是满二叉树
		if(i < n)
		{
			res = false;
			break;
		}
		n+=n; //下一次结点翻倍
	}
	return res;
}

判断是否是完全二叉树：

（从上到下、从左到右的顺序进行编号，若编号为i(1≤i≤n)的结点与满二叉树编号为i的结点位置相同，则此树称为完全二叉树）

利用其性质，从上到下、从左到右入队和出队，若其没有孩子入NULL；若出队时遇到NULL，则队列的剩余部分都应为NULL。

bool Is_Comp_Tree(BtNode* ptr)
{
	bool res = true;
	if(NULL == ptr)
		return res;
	queue<BtNode*> qu;
	qu.push(ptr);
	while(!qu.empty())
	{
		ptr = qu.front();
		 qu.pop();
		if(NULL == ptr)
			break;
		qu.push(ptr->leftchild );
		qu.push(ptr->rightchild );
	}
	//此时队列的剩余值应都为空
	while(!qu.empty())
	{
		ptr = qu.front();
		qu.pop();
		if(ptr != NULL)
		{
			res = false;
			break;
		}
		return res;
	}
}