排序 - - - 插入排序（直接插入排序、希尔排序）

插入排序：

基本思想：每次将一个待排序的元素，按其元素的大小插入到前面已经排好序的序列的适当位置，直到全部元素插完成为止。

---

直接插入排序：

基本思想：把n个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含一个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，把它的排序码依次与有序表元素的排序码进行比较，将它插入到有序表中的适当位置，使之成为新的有序表。

 效率分析：首先从空间来看，它只需要一个元素的辅助空间，用于元素的位置交换，空间复杂度O(1)。从时间分析，首先外层循环要进行n-1次插入, 每次插入最少比较一次(正序), 移动0次;最多比较i次(包括同监视哨R[0]的比较),移动i＋1次(逆序)(i=2,3,…,n)。因此，直接插入排序的时间复杂度为O（n2）。

直接插入算法的元素移动是顺序的，该方法是稳定的。

void InsertSort(int *arr, int len)
{
	int tmp = 0;
	for(int i = 1; i < len-1; ++i)
	{
		tmp = arr[i]; //保存无序序列第一个元素
		int j = i-1;
		//同有序序列最后一个元素比较，如果无序序列第一个元素小于有序序列最后一个元素，则后移
		while(j >= 0 && arr[j] > tmp)
		{
			arr[j+1] = arr[j];
			--j;
		}
		arr[j+1] = tmp;//找到无序序列第一个元素的合适位置，插入
	}
}

---

 

希尔排序：

基本思想：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率上有较大提高。

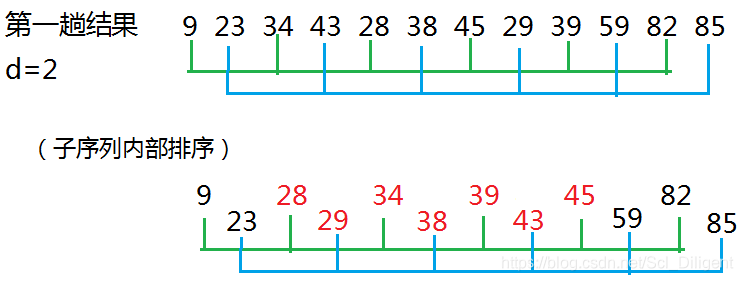
效率分析：虽然我们给出的算法是三层循环，最外层循环为log2n数量级，中间的for循环是n数量级的，内循环远远低于n数量级，因为当分组较多时，组内元素较少；此循环次数少；当分组较少时，组内元素增多，但已接近有序，循环次数并不增加。因此，希尔排序的时间复杂性在O（nlog2n）和O（n2 ）之间，大致为O（n1. 3）。

 由于希尔排序对每个子序列单独比较，在比较时进行元素移动，有可能改变相同排序码元素的原始顺序，因此希尔排序是不稳定的。

//子序列内部排序
void Shell(int* arr, int len, int dk)
{
	int tmp = 0;
	for(int i = dk; i < len-1; i += dk)
	{
		tmp = arr[i];
		int j = i-dk;
		while(j >= 0 && tmp < arr[j])
		{
			arr[j+dk] = arr[j];
			j -= dk;
		}
		arr[j+dk] = tmp;
	}
}
void ShellSort(int* arr, int len, int* dk, int dklen)
{
	for(int i = 0; i < dklen; ++i)
	{
		Shell(arr, len, dk[i]);
	}
}