python数据分析从入门到进阶：线性回归和正则化

最新推荐文章于 2025-05-20 15:57:16 发布

Python_P叔

最新推荐文章于 2025-05-20 15:57:16 发布

阅读量451

点赞数

CC 4.0 BY-SA版权

文章标签： python 数据分析线性回归

本文链接：https://blog.youkuaiyun.com/Saki_Python/article/details/133016095

本文介绍了Python中的线性回归及其正则化方法，包括岭回归、Lasso回归和早期停止策略。通过实例展示了如何实现和评估这些方法，探讨了它们在减少过拟合和提高模型解释性方面的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

引言

上一章中我们以minist数据集演示了如何实现一个分类算法，并进行选择。这一章中，我们将介绍广义线性模型。广义线性模型是机器学习的基础部分，也是很多其他算法的延伸。本文主要介绍一下如何实现简单的线性回归和正则化方法

🍅1.线性回归

通常，线性回归通过简单计算输入特征的加权和，加上一个称为偏差项（也称为截距项）的常数来进行预测。具体公式如下:

y^=β0+β1X1+…+βnXn\hat{y}=\beta_0 + \beta_1 X_1+…+\beta_n X_ny^=β0+β1X1+…+βnXn

接下来我们看看具体如何实现线性回归模型

import numpy as np
import matplotlib.pyplot as plt

# 生成模拟数据集
X = np.random.randn(100,1)
y = 3*X+4+np.random.randn(100,1)

观察一下生成的数据集

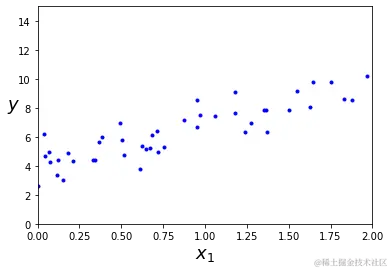
output_5_0

plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.savefig("generated_data_plot")
plt.show()

可以看出数据呈现比较明显的线性趋势，下面使用LinearRegression实现对线性模型的训练

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
a = lin_reg.intercept_
b = lin_reg.coef_
a,b#回归系数和截距

(array([3.86880209]), array([[3.0229374]]))

下面根据训练好的线性回归模型进行预测，

X_new = np.array([[0], [2]])
y_predict = lin_reg.predict(X_new)
y_predict

array([[3.86880209],
       [9.91467688]])

将预测结果可视化如下

plt.plot(X_new, y_predict, "r-", linewidth=2, label="Predictions")
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 2, 0, 15])
plt.show()

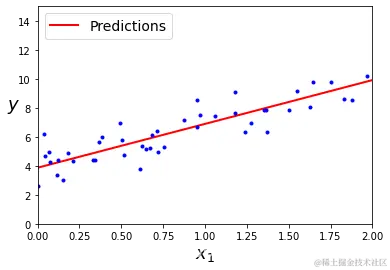
请添加图片描述

可以看出拟合结果还不错，下面我们绘制一下Learning curve：随着模型训练样本的变化观察训练集和测试集的误差

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
'''
定义learning_curves函数
'''
def plot_learning_curves(model, X, y):
    X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)#将数据分为训练集合验证集
    train_errors, val_errors = [], []#定义训练误差和验证误差
    for m in range(1, len(X_train) + 1):
        model.fit(X_train[:m], y_train[:m])#根据训练集大小训练模型
        y_train_predict = model.predict(X_train[:m])#拟合训练集
        y_val_predict = model.predict(X_val)#拟合验证集
        train_errors.append(mean_squared_error(y_train[:m], y_train_predict))#计算训练集MSE
        val_errors.append(mean_squared_error(y_val, y_val