收益率随机变量特征以及组合风险的一种几何直观解释

最新推荐文章于 2022-05-18 18:47:33 发布

S_o_l_o_n

最新推荐文章于 2022-05-18 18:47:33 发布

阅读量2k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：量化投资

本文链接：https://blog.youkuaiyun.com/S_o_l_o_n/article/details/100728961

量化投资专栏收录该内容

25 篇文章

订阅专栏

本文从几何角度解读随机变量，将其视为无穷维向量，解释期望、标准差、协方差及组合风险的几何意义，提供资产风险贡献的直观理解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

说明：由于本文是从投资的角度展开的，所以其中涉及的所有随机变量都表示收益率随机变量。由于本文旨在给收益率随机变量特征以及组合风险提供一个几何直观，因此文中的部分陈述可能会缺失一些严谨性。

从几何的角度去推导代数上的资产风险贡献定义

结语

随机变量的向量表示

当我们对两个随机变量计算协方差和方差的时候，可以发现，其形式和向量的点积是很类似的，实际上，如果把随机变量看作是一个无穷维向量的话，期望运算实际上是满足内积定义的，此时定义了期望运算的随机向量构成的线性空间就成了内积空间，如果我们再把风险sigma定义为范数的话，那么其就是一个线性赋范空间。把随机变量看成无穷维向量，进而从线性赋范空间的角度去看待随机变量线性空间，是很有助于我们从几何的角度去理解收益率随机变量中的收益、风险、相关系数等重要特征。具体来讲，当我们把一个随机变量看成一个向量时，这个向量的一个坐标就是一次独立试验得到的随机变量的realization，那么为什么需要是无穷维的呢？这是因为根据大数定律，期望是相应样本关系式的极限值，所以我们需要无穷多维向量才能准确的表示一个随机变量。

期望向量

这里的期望向量指的是由随机变量的期望值作为坐标的无穷维向量，显然，这样的向量的各个坐标值相等，所以其是一个常量，而且其在直线x1=x2=x3=...=xn=...上，记为直线l。根据大数定律，期望等于样本点均值的极限值，所以一个无穷维向量对应的期望向量就是该向量在直线l上的投影向量。

中心化向量

所谓中心化向量就是对一个中心化之后的随机变量的向量化表示，所以中心化向量的坐标和一定是为0的。对于一个向量，其中心化向量就是该向量和其期望向量的矢量差。

中心化向量的角色是核心的，因为无论是方差、协方差还是相关系数，都要用到中心化向量。

几何直观展示

严格来说，为不失一般性，一个随机变量应该用一个无穷维的向量来表示。但是为了可以直观展示，我们这里只用三维的空间向量来展示，虽然维度只有三维，但是其向量的本质并没有改变，相关的不涉及具体维数的结论也不会改变。所以下面我们用三维的空间向量对我们之前的概念进行一个展示，如图一。

图一中，向量OD和OE表示两个随机变量，OC在直线l上，向量OI为向量OD和OE的矢量和，所以OI就相当于OD和OE组成的投资组合。点F,G,M为各个向量在OC上的投影，可知向量OF,OG,OM分别为期望向量，所以FD,GE,MI分别为中心化向量。通过简单的向量运算，易知向量MI等于FD和GE的矢量和。

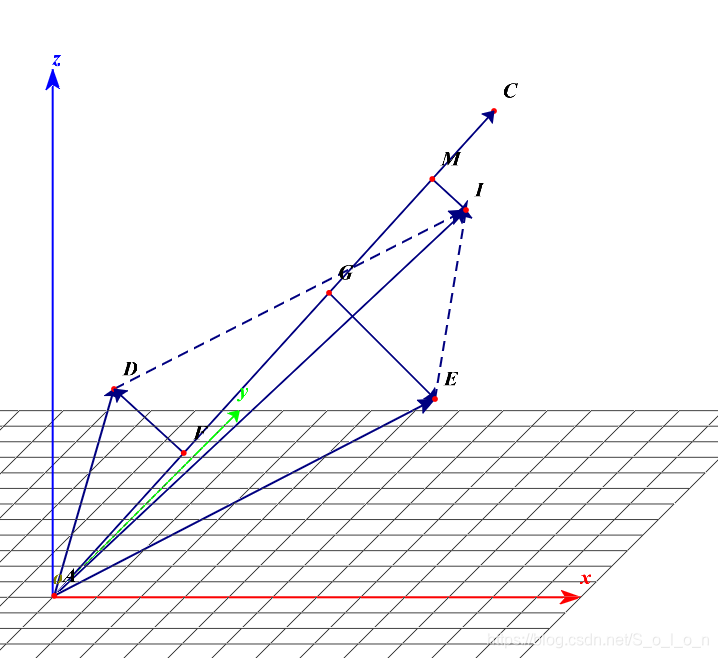
图一

期望、标准差、协方差和相关系数的几何表示

显然，期望为期望向量的模scaled by square root of n，其中n表示维数；标准差为中心化向量的模scaled by square root of n；两个随机变量的协方差为对应的两个中心化向量的内积scaled by n。由于n对于每个向量来说都是一样的，所以当我们进行期望、标准差、协方差的比较时，直接可以忽略掉n，换言之，我们只要不计算绝对的值，就可以用期望向量的模衡量期望的绝对值大小，用中心化向量的模衡量标准差大小，用向量积来衡量协方差大小。

所以，如果要比较哪个向量具有更高的收益风险比，只需要找和直线l夹角最小的那个向量即可，因为该夹角越小，收益风险比越大。在直线l上的中心化向量为0向量，即方差为0，这也是显然的，因为前面我们已经说过，在该直线上的向量代表的是一个常量。

根据相关系数的定义可知，其等于两个中心化向量的内积和其模的乘积的比值，再根据向量内积的定义，两个向量的相关系数就等于其对应中心化向量夹角的余弦值。

组合风险贡献的几何表示

假设我们有一个两个资产组成的投资组合，那么如何衡量每个资产对这个组合的风险贡献呢？延续上面的概念和定义，我们可以很直观的得到如何表示资产对组合的风险贡献。

如下图，向量NO和NP表示两个资产收益的中心化向量，NQ表示其矢量和，可知NQ就是该组合的中心化向量。根据前述，我们知道中心化向量的模可以衡量对应随机变量的标准差，即风险，所以分量在组合中心化向量上的分解或者投影代表对组合中心化向量的贡献，各分量对应的模就是子资产对组合风险的贡献度，如图中的NW和WQ。可知，子资产的风险贡献之和就等于组合的总风险，这样定义风险贡献是很直观和合理的。

而根据向量内积的定义，我们可知，给定权重的资产收益率的中心化向量在组合中心化向量上的投影等于两者的内积除以组合中心化向量的模，即：

$risk\_contribution\_1=\frac{w_{i}\cdot \overrightarrow{ r_{i\_cen}}\cdot\overrightarrow{r_{p\_cen}} }{\left | \overrightarrow{r_{p\_cen}} \right |}=\frac{w_{i}\cdot cov(r_{i},r_{p})}{\sigma _{p}}$

组合风险在代数和几何上的一致性推导

从代数上，根据余弦定理，可得：

$\sigma _{p}^{2}=w_{1}^{2}\cdot \sigma _{1}^{2}+w_{2}^{2}\cdot \sigma _{2}^{2}+2w_{1}w_{2}\sigma _{1}\sigma _{2}\cdot cos\alpha$

因为前面已经说过，两个中心化向量夹角的余弦值就等于其相关系数，所以上式又可以写成：

$\sigma _{p}^{2}=w_{1}^{2}\cdot \sigma _{1}^{2}+w_{2}^{2}\cdot \sigma _{2}^{2}+2w_{1}w_{2}\cdot cov(r_{1},r_{2})$

该等式正是对组合方差的计算公式，这里从几何意义的组合风险到代数上的组合风险的一致性推导进一步验证了我们这种几何表示的合理性。

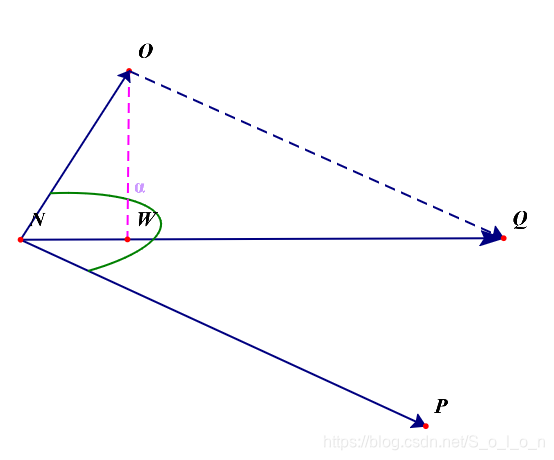
图二

从几何的角度去推导代数上的资产风险贡献定义

在代数上，资产i对组合的风险贡献的定义为 $w_{i}\cdot\frac{\partial \sigma(w) }{\partial w_{i}}$ , 等于该资产的权重和边际风险贡献的乘积。直接从代数上理解该定义，其实并没有那么简单，因为该偏导并不是常数，所以在此我们可以从几何的角度去理解和推导这个定义。

如下图，令向量YZ表示随机收益率变量 $w_{i}\cdot r_{i}$ 的中心化向量，其中 $w_{i}$ 表示在该资产上的权重；现假设我们要计算资产i对组合的风险贡献，根据前述可知，其风险贡献就等于向量YZ在向量XZ上的投影的模，即图中向量D1Z的模。现在我们已知向量YZ的模为 $w_{i}\cdot \sigma _{i}$ ， $\sigma _{i}$ 表示资产i的标准差，那么只需要知道该中心化向量和组合中心化向量的(向量XZ)夹角的余弦值即可，这样两者的乘积便是投影，也即资产i对组合的风险贡献。

所以关键在于如何求夹角的余弦值。如下图，我们利用微元法，假设在资产i上的权重变化 $\Delta w_{i}$ ，则资产i的风险，也即其中心化向量的模变化 $\Delta w_{i}\cdot \sigma _{i}$ ，其在组合风险上的分量为 $\Delta \sigma _{i}$ ，如图红色线所示。所以我们可得：

$cos\theta =\frac{\Delta \sigma }{\Delta w_{i}\cdot \sigma _{i}}=\frac{\partial \sigma (w)}{\partial w_{i}\cdot \sigma _{i}}$

所以资产i的风险贡献为：

$risk\_contribution\_2=w_{i}\cdot \sigma _{i}\cdot cos\theta =w_{i}\cdot \sigma _{i}\cdot \frac{\partial \sigma (w)}{\partial w_{i}\cdot \sigma _{i}}=w_{i}\cdot \frac{\partial \sigma (w)}{\partial w_{i}}$

至此，我们从几何的角度推导出了资产风险贡献的代数定义。而且，从纯几何角度定义得到的风险贡献risk_contribution_1和从代数角度定义的risk_contribution_2在这里也从几何的角度得到了完全的等价证明，即两者的定义是完全等价的。

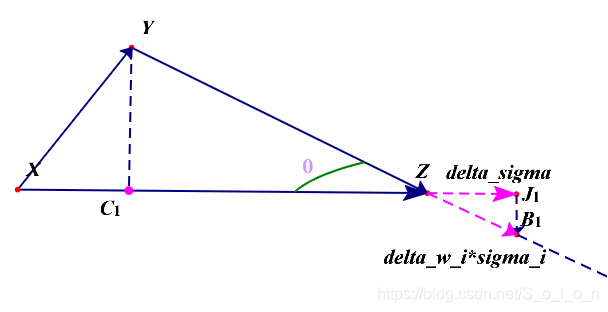
图三

结语

本文从几何的角度给随机变量提供了一个表征，通过将随机变量表征为一个无穷维向量的方式来几何化，从而给随机变量的特征和随机变量之间的关系提供了一个几何直观，特别的，从组合风险管理的角度，提供了资产风险贡献的一个几何表征，并且证明了几何和代数上的等价性。随机变量的几何化可以给我们提供一个强有力的直观，这对我们在对收益率风险特征的理解以及投资组合风险管理上提供了一个新的角度，可以让我们更好的理解某些结论，甚至有时候可以从直观上给我们提供一些新的思路和想法。