深度优先搜索（一）—— 数独、部分和、八连通水洼

dfs基本概念

what ？： 深搜是从某一状态开始，不断的转移状态直到无法转移，然后回退到前一个状态，继续转移到其他状态，如此不断的重复，直到得到最终解； 一般dfs与递归结合解题。
回溯：递归调用代表开启一个分支，如果希望这个分支返回后某些数据恢复到分支前的状态以便重新开始，就要用回溯技巧。
剪枝：dfs时，如果已明确从当前状态无论如何转移都不会存在（更优）解，就应该中断往下继续搜索，称为剪枝。

例子

数独

import java.util.Scanner;
public class Main {
		public static void main(String[] args) {
		  char [][]table = new char[9][];
		   int x=0,y=0;
		   Scanner scanner = new Scanner(System.in);
		   for(int i=0;i<9;i++)
		      table[i] = scanner.nextLine().toCharArray();
           dfs(table,x,y);
       }

		private static void dfs(char[][] table, int x, int y) {
			if(x == 9){
				print(table);
				System.exit(0);   //退出
			}		
			if(table[x][y] == '0'){
				for(int i = 1;i < 10;i++){
					boolean res = check(table,x,y,i);
					if(res == true){
						table[x][y] = (char) ('0'+ i);
					    dfs(table,x+(y+1)/9,(y+1)%9); //转移状态
					}
				}
				table[x][y] = '0';//回溯
			}
			else{
				dfs(table,x+(y+1)/9,(y+1)%9);
			}		
		}

		private static void print(char[][] table) {
			for(int i=0;i<9;i++){
				for(int j=0;j<9;j++){
					System.out.print(table[i][j]);
				}
				System.out.println();
			}			
		}

		private static boolean check(char[][] table, int x, int y, int i) {
            for(int k=0;k<9;k++){
            	if(table[x][k] == (char)('0' + i))  return false;
                if(table[k][y] == (char)('0' + i))  return false;
            }
            for(int k=(x/3)*3;k<(x/3+1)*3;k++){
            	 for(int m=(y/3)*3;m<(y/3+1)*3;m++){
            		 if(table[k][m] == (char)('0' + i))  return false;		 
            	 }
            }
			return true;
		}	
}

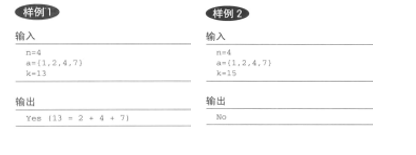
例：输入

输出

部分和问题

可以用求解非空子集（二进制迭代）的方法解（是解此问题的最优方法）.
这里就用dfs和dp分别实现。

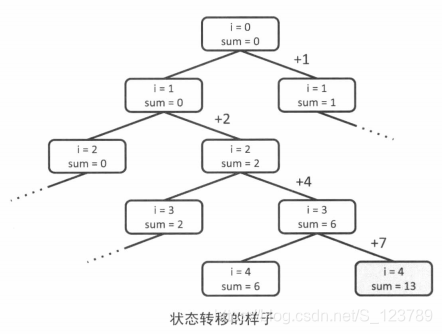
dfs
思路

import java.util.ArrayList;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {		     
              Scanner scanner = new Scanner(System.in);
              int n = scanner.nextInt();
              int []arr = new int[n];
              for(int i =0;i<n;i++)
            	  arr[i] = scanner.nextInt();
              int k = scanner.nextInt();
              int kk = k;
              dfs(arr,k,0,new ArrayList<Integer>(),kk);
 //new ArrayList<Integer>()相当于ArrayList<Integer> sn = new ArrayList<>();
	}

	private static void dfs(int[] arr, int k, int cur, ArrayList<Integer> s, int kk) {
		if(k==0){
			System.out.print ("Yes("+kk+"=");
			for(int i = 0;i<s.size();i++){
			  System.out.print(s.get(i));
			  if(i < s.size()-1)
			   System.out.print("+");
			}
			System.out.print(")");
			System.exit(0); //当只需一个解时   
			//当需要显示它所有可能解时，就要使用return      
		}
		if(arr.length == cur || k<0)  return;  
		dfs(arr,k,cur+1,s,kk);
		
		s.add(arr[cur]);
		int index = s.size()-1;
		dfs(arr,k-arr[cur],cur+1,s,kk);  //要arr[]这个值
		s.remove(index);  //回溯
	}
}

dp

//部分和
public class dp {
    static int[] arr = {3,4,5,6,9};
    static int s = 8;
    static boolean [][]table = new boolean[5][s+1];
	public static void main(String []args){
		fun(s);
		System.out.print(table[arr.length-1][s]);	
 }

	private static void fun(int s) {
		   
		for(int i1=0;i1<arr.length;i1++)
		   table[i1][0] = true;
		
		for(int i1=1;i1<=s;i1++)
			   table[0][i1] = false;		
		
		if(arr[0]<=s)
			table[0][arr[0]] = true;
		
		boolean A=false,B=false;
		for(int i=1;i<arr.length;i++){
			for(int j=1;j<=s;j++){
				if(arr[i]>j)  table[i][j] = table[i-1][j];
				else{
					A = table[i-1][j];
					B = table[i-1][j-arr[i]];
					table[i][j] = A||B;
				}
			}
		}		 
	}
}

八连通水洼 解法一

八连通积水为一个水洼

思路
从任意的‘w’开始，不断的把‘w’替换为’.’（以一个水洼为单位），1次dfs就把与’w’连接的部分都替换为了‘.’，直到园子里没有‘w’.那么总共的dfs次数就是水洼个数。

import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
              int res=0;
		      char arr[][] = new char[10][];
              Scanner scanner = new Scanner(System.in);
              for(int i=0;i<10;i++){
            	  arr[i] = scanner.nextLine().toCharArray();
              }
               for(int i=0;i<10;i++){
            	   for(int j=0;j<12;j++){
            		   if(arr[i][j] == 'w'){
            			   dfs(i,j,arr);
            		        res++;
            		   }
            	   }
               }
               System.out.print(res);
      	}

	private static void dfs(int i, int j,char [][]arr) {
		arr[i][j] = '.';
		for(int dx=-1;dx<=1;dx++){
			for(int dy=-1;dy<=1;dy++){
				int nx = i+dx,ny=j+dy;
				if(nx < 10 && ny <12 && nx>= 0 && ny>=0 && arr[nx][ny] == 'w')
						dfs(nx,ny,arr);
			}
		}
	}
}

八连通水洼 解法二

import java.util.Scanner;
public class Main{
	static int cnt;
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		char [][]graph = new char[10][12];
		for(int i=0;i<10;i++)
		    graph[i] = sc.nextLine().toCharArray();
	    
		for(int i =0;i<10;i++){
			for(int j=0;j<12;j++){
				if(graph[i][j] == 'w'){
					dfs(graph,i,j);
					cnt++;
				}
			}
		}
		System.out.print(cnt);
		
	}
	private static void dfs(char[][] graph, int i, int j) {
		if(i<0 || i>=10 || j<0  || j>=12)  return;
		
		//当不是w
		if(graph[i][j] == '.')  return;
		
		graph[i][j] = '.';
		
		//八个方向去探测
		dfs(graph,i,j-1);
		dfs(graph,i,j+1);
		dfs(graph,i-1,j-1);
		dfs(graph,i-1,j+1);
		dfs(graph,i+1,j+1);
		dfs(graph,i+1,j-1);
		dfs(graph,i+1,j);
		dfs(graph,i-1,j);
	}
}

其实 八连通水洼这个题中 将 w 直接替换成 . 等同于 创建一个标记数组解决。

问题

部分和问题 使用求非空子集的方法 实现，后面补充。

小结

数独 和 部分和用到了回溯，水洼 存在状态互相转移的问题，巧妙的将 w 换成 . 就可以避免。