递推/DP(动态规划)UVA 10081-Tight Words

最新推荐文章于 2024-10-01 18:52:56 发布

Cai-Crayon

最新推荐文章于 2024-10-01 18:52:56 发布

阅读量295

点赞数

CC 4.0 BY-SA版权

分类专栏：递推 DP 文章标签：动态规划递推 UVA 10081 Tight Words UVA 10081-Tight Words

本文链接：https://blog.youkuaiyun.com/SZU_Crayon/article/details/81813970

DP 同时被 2 个专栏收录

4 篇文章

订阅专栏

递推

2 篇文章

订阅专栏

本文介绍了一个通过动态规划解决的概率问题——UVA10081-TightWords。该问题要求计算由0到k的数字构成的长度为n的序列中，相邻数字差距不大于1的概率。文章提供了详细的解题思路及完整的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

递推/DP(动态规划)UVA 10081-Tight Words

题目链接：10081 - Tight Words
思路：

题目大意是有一个序列长度为n，是由0~k组成的，问得到序列相邻数字差距不大于1的概率是多少

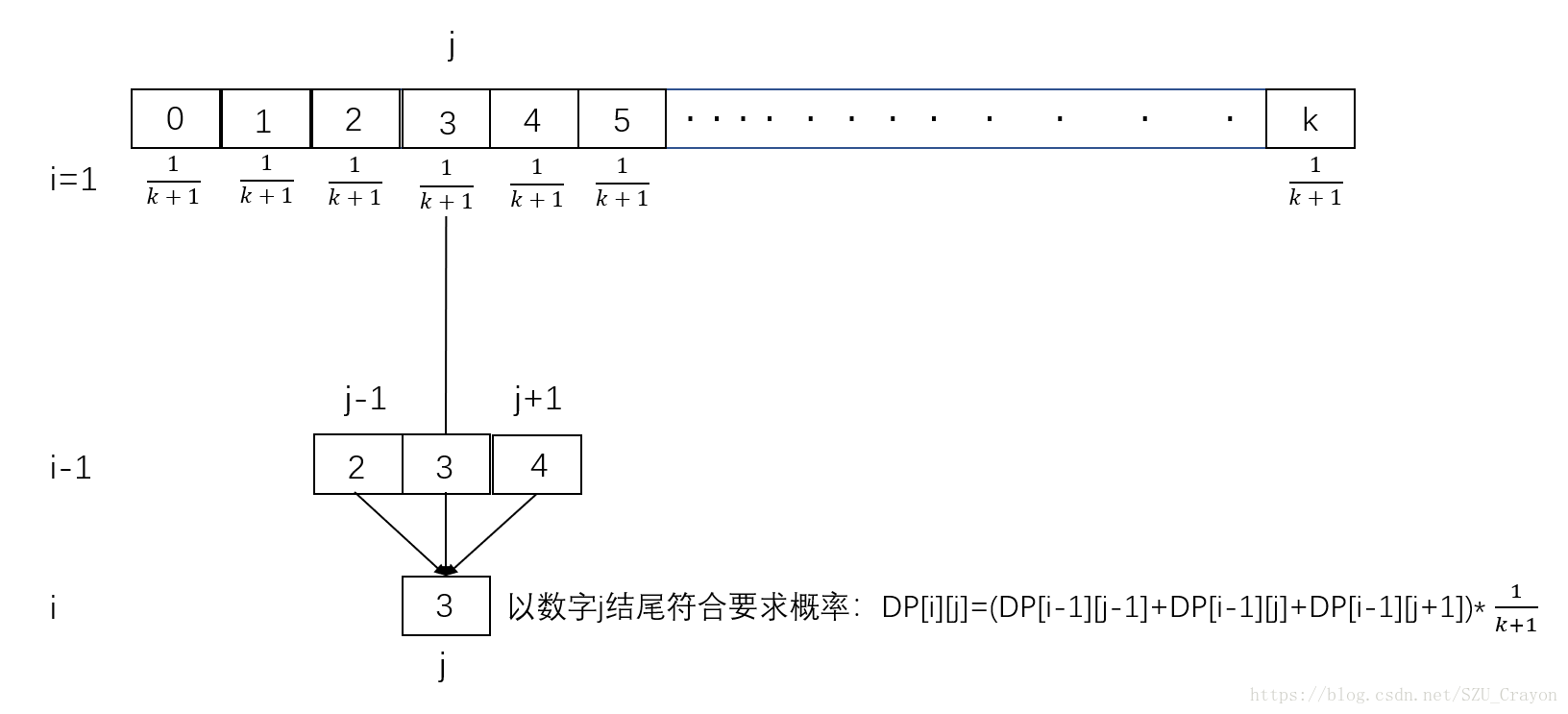
假设目前已经排好了前 i-1个数字，目前要排第i个数字，并且第i个数字是 j，那么第i个数字与相邻（也就是第i-1个数字）差距不大于的情况只有当i-1个数字为：j >=0 下的j-1，j，j+1，把长度i-1序列可能情况概率加起来乘上 1/(k+1)---因为第i个数字为j的概率为 1/(k+1)

DP初态是i=1时，这个时候数字为j（j>=0,j<=k）的概率为 1/(k+1)

代码：

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;

int main()
{
    int k,n;
    while(cin>>k>>n)
    {
        double DP[105][10]={0};
        double Res=0.0;
        for(int i=0;i<=k;i++)
            DP[1][i]=1.0/(k+1);
        for(int i=2;i<=n;i++)
        {
            for(int j=0;j<=k;j++)
            {
                for(int l=0;l<=k;l++)
                    if(abs(l-j)<=1)   //ok
                    {
                        DP[i][j]+=DP[i-1][l]*(1.0/(k+1));
                        //cout<<DP[i][j]<<endl;
                    }
            }
        }
        for(int i=0;i<=k;i++)
            Res+=DP[n][i];
        cout<<fixed<<setprecision(5)<<Res*100<<endl;
    }
    return 0;
}