树的相关知识

树的邻接表存储

const int N=1e5+10;
int tot; //边的编号，从0开始，奇数为正向边，偶数为反向边
int ver[2*N]; //下标为边的编号，存储的是 某条边 到达 哪个点
int edge[2*N];//下标为边的编号，存储的是 某条边 的权值
int Next[2*N];//下标为边的编号，存储的是 某条边 （作为某个点的出边集合中）的下一条边的编号
int head[N];  //下标为节点的编号，存储的是 某个节点（的出边集合中）的第一条边的编号
int pre[N];   //下标为节点的编号，存储的是 某条节点 是通过哪条边到达的

void add(int x, int y, int z) {
    ver[++tot] = y; //存到达点
    edge[tot] = z;  //存边的权值
    Next[tot] = head[x]; //新读入的边 设置 起点的第一条出边编号 作为自己的下一条边
    head[x] = tot; //新读入的边插队
}

int main() {
    cin >> n;
    for(int i = 1; i < n; i++) {
        int x,y;
        cin >> x >> y;
        add(x, y, 1);
        add(y, x, 1);
    }

    return 0;
}

树的DFS

void dfs(int x) {
	vis[x] = 1;
	for(int i = head[x]; i; i = Next[i]) {
		int y = ver[i];
		if(vis[y]) continue;	//因为无向图边会正反存两次 
		dfs(y);
	}
}

树的时间戳

void dfs(int x) { 
	dfn[x] = ++cnt;
	for(int i = head[x]; i ; i = Next[i]) {
		int y = ver[i];
		if(dfn[y]) continue;
		dfs(y);
	}
}

树的DFS序

void dfs(int x) {
	a[++m] = x; //存储dfs序，进入
	vis[x] = 1;
	for(int i = head[x]; i; i = Next[i]) {
		int y = ver[i];
		if(vis[y]) continue;
		dfs(y);
	}
	a[++m] = x; //存储dfs序，离开
}

树的深度

void dfs(int x) {
	vis[x] = 1;
	for(int i = head[x]; i; i = Next[i]) {
		int y = ver[i];
		if(vis[y]) continue;
		d[y] = d[x] + 1; //计算深度
		dfs(y);
	}
}

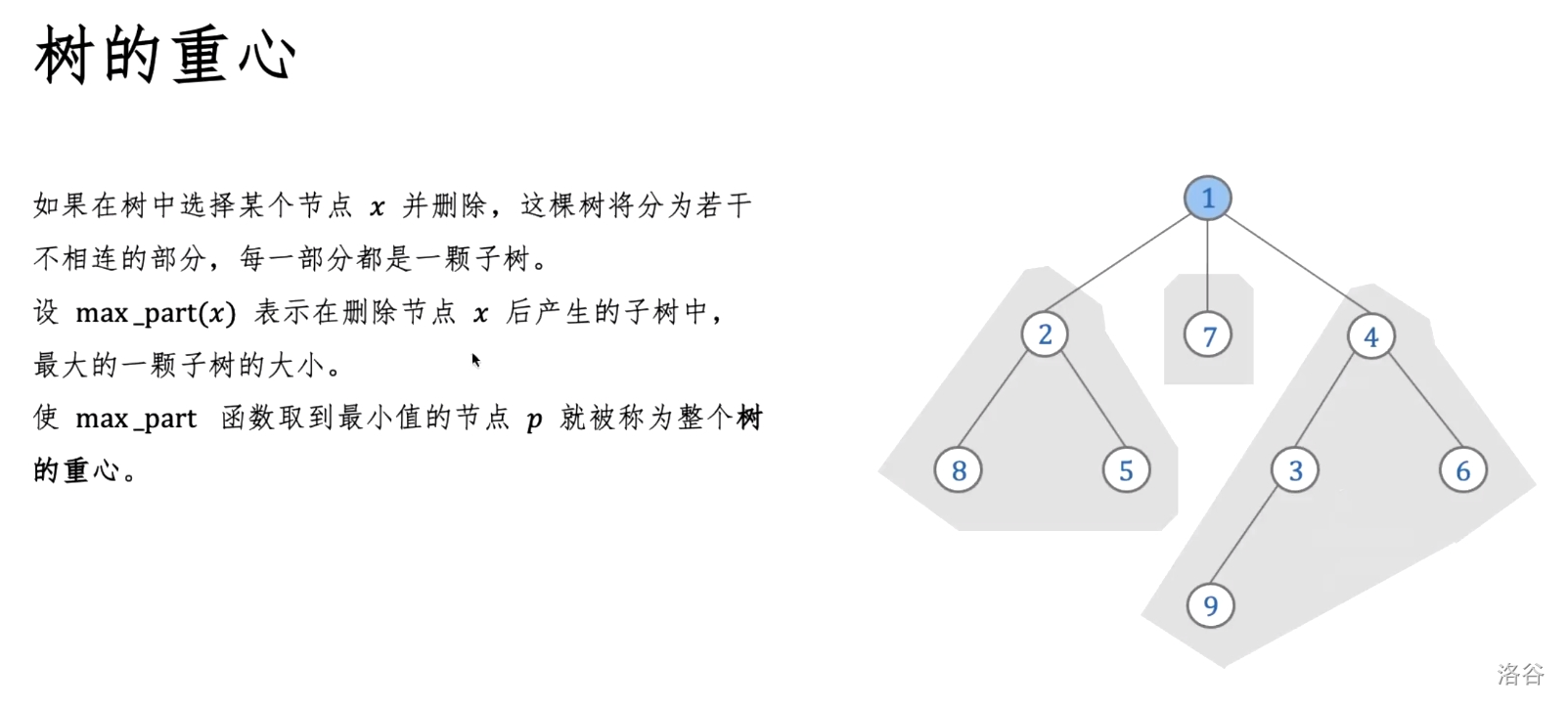
树的重心

void dfs(int x) {
	vis[x] = 1;
	size[x] = 1; //子树的大小，默认为自身一个节点
	int max_part = 0; 
	for(int i = head[x]; i; i = Next[i]) {
		int y = ver[i];
		if(vis[y]) continue;
		dfs(y);
		size[x] += size[y]; //从子节点向父节点递推
		max_part = max(max_part, size[y]);
	}
	max_part = max(max_part, n - size[x]); //n为整棵树的节点数量
	if(max_part < ans) {
		ans = max_part; //全局变量 ans 记录重心对应的 max_part
		pos = x; //全局变量 pos 记录重心
	}
}

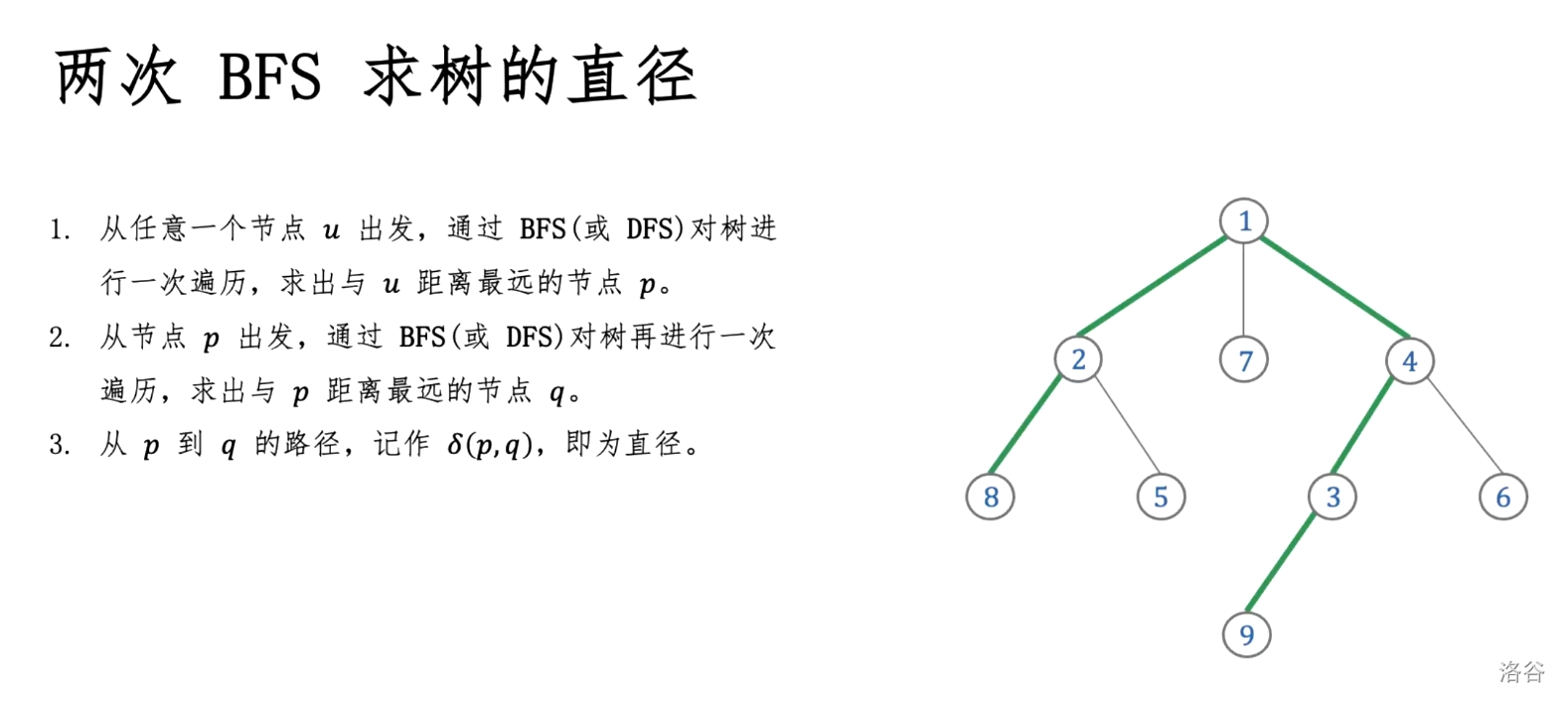
树的直径

BFS求树的直径

int bfs(int t) {
    memset(v,0,sizeof(v));
    memset(dis,0,sizeof(dis));
    queue<int>q;
    q.push(t);
    v[t] = 1;
    int maxx = 0;
    int index = t;
    while(q.size()) {
        int x = q.front(); q.pop();
        for(int i = head[x]; i; i = Next[i]) {
            int y = ver[i];
            if(!v[y]) {
                dis[y] = dis[x] + edge[i];
                if(dis[y] > maxx){
                    maxx = dis[y];
                    index = y;
                }
                v[y] = 1; q.push(y);
            }
 
        }
    }
    return index;
}

// int main(){}
    int T1=bfs(1);
    int T2 = bfs(T1);

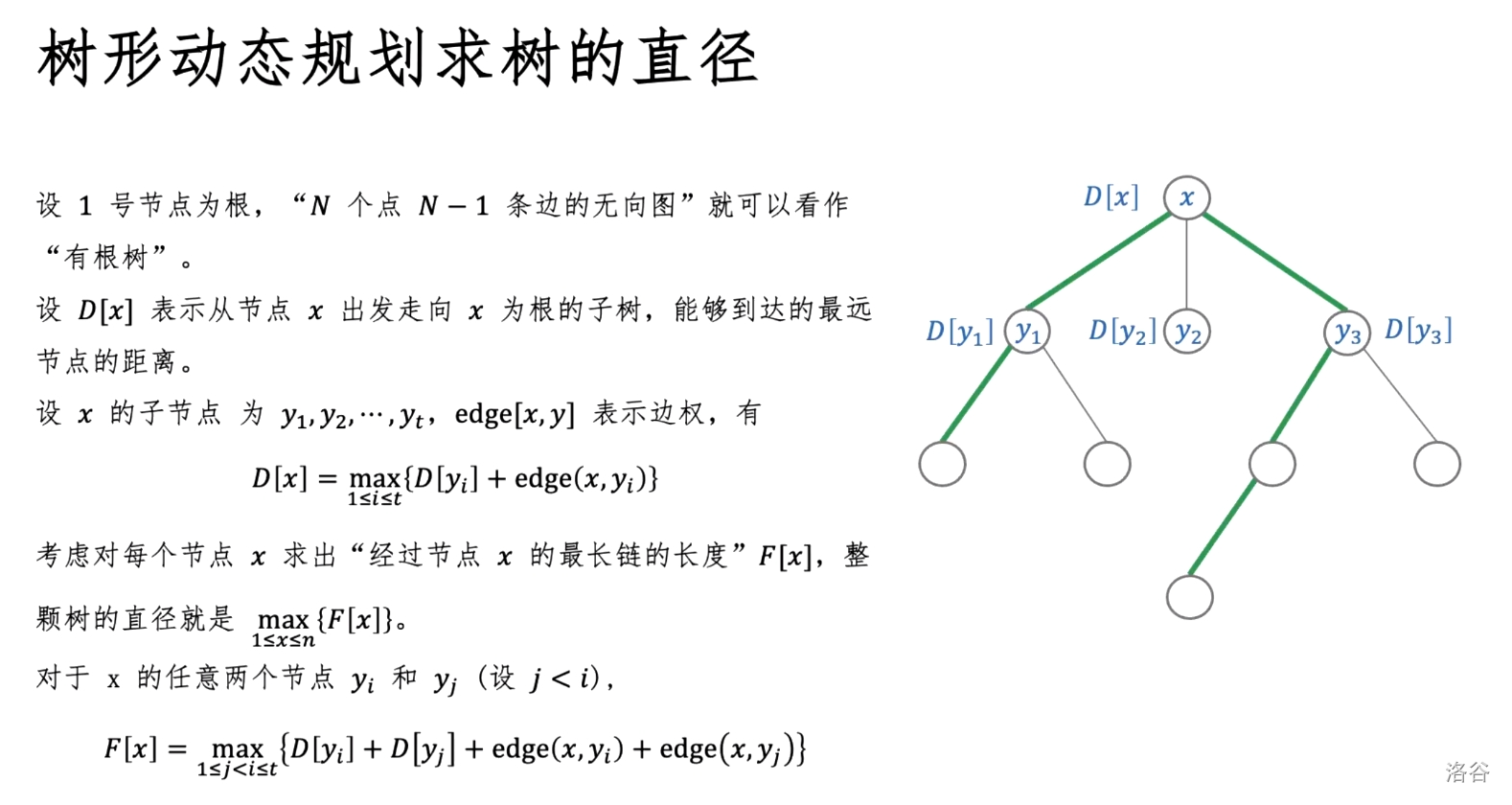
树形DP求树的直径

int ans = 0;
void dp(int x) {
    v[x] = 1;
    for(int i = head[x]; i; i = Next[i]) {
        int y = ver[i];
        if(v[y]) continue;
        dp(y);
        ans = max(ans, d[x] + d[y] + edge[i]);
        d[x] = max(d[x], d[y] + edge[i]);
    }
}