单调栈模版题

题目描述

给出项数为 n 的整数数列a1…n​。

定义函数 f(i) 代表数列中第 i 个元素之后第一个大于 ai​ 的元素的下标，若不存在，则 f(i)=0。

试求出 f(1…n)。

输入格式

第一行一个正整数 n。

第二行 n 个正整数 a1…n​。

输出格式

一行 n 个整数表示 f(1),f(2),…,f(n) 的值。

典型的单调栈模版题

首先,我先来说一下什么是单调栈

单调栈,顾名思义,就是一个保持单调性的栈,这时大体分为两种,单调递增和单调递减

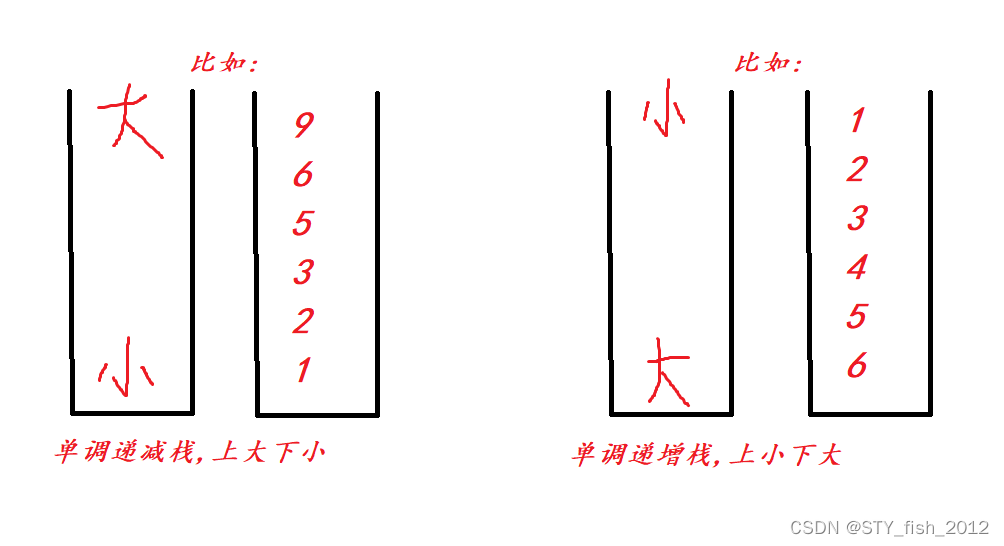
那么,这道题我们要用一个什么栈呢?

单调递增栈 

因为是看右边,所以说我们入栈的时候要倒过来

那么,这个时候,比ai小的元素就没用了,所以,栈顶如果比ai小,就踢掉

while(head>0&&a[t[head]]<=a[i])head--;

执行完上面的程序,现在栈中的栈顶元素就是第一个比a[i]大的值了

把栈顶存入另一个栈 k 中(因为我们是到这入栈的,所以输出得反过来),这里要注意,如果head==0,就说明a[i]已经把所有元素都噶掉了,就将0压入k里面,否则就是将n-t[head]+1压入k(因为这里是倒着来的)

接着就是把 i 入栈

if(head==0)k.push(0);
		else k.push(n-t[head]+1);
		t[++head]=i;

最后每个元素都入栈了,就将k中的元素输出

while(!k.empty()){
	printf("%d ",k.top());
	k.pop();
}

完整代码如下:

#include<bits/stdc++.h>
using namespace std;
const int N=3e6+5;
int a[N];
int t[N];
int n;
int head;
signed main(){
	scanf("%d",&n);
	for(int i=n;i>=1;i--)scanf("%d",&a[i]);
	stack<int> k;
	for(int i=1;i<=n;i++){
		while(head>0&&a[t[head]]<=a[i])head--;
		if(head==0)k.push(0);
		else k.push(n-t[head]+1);
		t[++head]=i;
	}
	while(!k.empty()){
		printf("%d ",k.top());
		k.pop();
	}
}