机器学习-线性回归实战

理论推导参见机器学习-线性回归问题

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd 
        

import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt


#载入数据的两种方式，第一种不使用pandas里的方法
def loadDataSet(filename):
    with open(filename) as f:
        dataMat=[]
        labelMat=[]
        for line in f.readlines():
            data=line.strip().split('\t')
            dataMat.append(data[0:2])
            labelMat.append(data[-1])
            x=np.matrix(dataMat,dtype=float)#将list转为matrix
            y=np.matrix(labelMat,dtype=float).reshape(-1,1)
        return x,y



#第二种方式使用pandas里的方法
def loadDataSet2(filename):

    data=pd.read_csv(filename,sep='\t',header=None)

    #x,y返回是array类型
    # da=np.array(data)
    # x=da[:,0:2]
    # y=da[:,-1]

    #x,y最终是matrix类型
    cols = data.shape[1]
    X = data.iloc[:,0:cols-1]#X是所有行，去掉最后一列
    Y = data.iloc[:,cols-1:cols]#X是所有行，最后一列
    x = np.matrix(X.values)
    y = np.matrix(Y.values)

    #matrix和array的区别
    # 它俩都有shape属性，但是matrix只能是二维的，shape只有行和列属性，而array可以是n维的。 
    # 乘法： 
    # array的*就是对应元素相乘，如果行或列数不匹配会自动补全，这就是numpy的”广播”。 
    # array想要实现矩阵相乘，使用np.dot(array1, array2) 
    # matrix的*就是矩阵相乘。 
    # matrix想要实现对应元素相乘，使用np.multiply(mat1, mat2)
    return x, y

#求最优参数w的两种方法
#正规方程
def normalEqn(xArr,yArr):
    w=np.linalg.inv(xArr.T*xArr)*xArr.T*yArr
    return w

#梯度下降
def computeCost(x,y,w):
    eqn=np.power((x*w.T)-y,2)
    return np.sum(eqn)/2*len(x)



# computeCost(x,y,w)

def gradientDescent(x,y,w,alpha,iters):
    wj=np.matrix(np.zeros(w.shape))
    parameters=int(w.ravel().shape[1])#ravel()将多维数组降为一维
    cost=np.zeros(iters)
    
    for i in range(iters):
        error=(x*(w.T))-y
        for j in range(parameters):
            term=np.multiply(error,x[:,j])
#             term=error*x[:,j]
            wj[0,j]=w[0,j]-(alpha/len(x))*np.sum(term)
            
        w=wj
        cost[i]=computeCost(x,y,w)
    return w,cost

if __name__=='__main__':
    #这里调用的是梯度下降的方法
    x,y=loadDataSet2('ex0.txt')
    w=np.matrix(np.array([0,0]))
    alpha=0.01
    iters=1000
    w,cost=gradientDescent(x,y,w,alpha,iters)
    xArr=np.array(x)
    yArr=np.array(y)
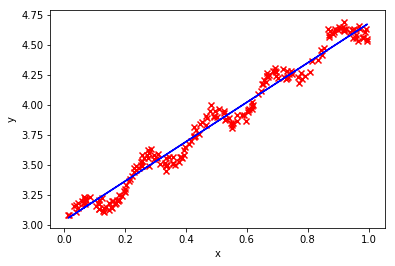
    plt.scatter(xArr[:,1],yArr[:,0],marker='x',color = 'r')
    plt.plot(xArr[:,1],xArr*w.T,color = "blue",linestyle = "-")
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()
    

#使用sklearn库里的方法进行线性回归
from sklearn import linear_model

x,y=loadDataSet2('ex0.txt')
model=linear_model.LinearRegression()
model.fit(x,y)
f=model.predict(xArr).flat
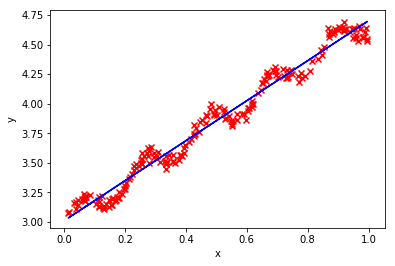
plt.scatter(xArr[:,1],yArr[:,0],marker='x',color = 'r')
plt.plot(xArr[:,1],f,color = "blue",linestyle = "-")
plt.xlabel('x')
plt.ylabel('y')
plt.show()