博弈论知识点总结（巴什博奕威佐夫博弈尼姆博弈 SG()函数介绍）

最新推荐文章于 2022-11-18 15:32:52 发布

原创最新推荐文章于 2022-11-18 15:32:52 发布 · 569 阅读

0 ·

CC 4.0 BY-SA版权

ACM 同时被 3 个专栏收录

137 篇文章

订阅专栏

(＾－＾) ------博弈论 -------(＾－＾)

19 篇文章

订阅专栏

4 篇文章

订阅专栏

本文深入解析了尼姆博弈中使用异或运算的原因，并提供了详细的SG函数实现模板，帮助读者理解游戏策略背后的数学原理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

转载自：总结

真心感谢博主，终于知道为什么尼姆博弈用异或来解决。

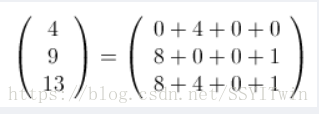
SG函数模板：

void init()//根据题目要求进行修改 
{
	a[0]=1;
	for(int i=1;i<=32;i++)
	   a[i]=a[i-1]*2;
}
void SG()
{

	for(int i=1;i<=1000;i++)
	{	
	    memset(vis,0,sizeof(vis));
		for(int j=0;a[j]<=i;j++)
		{
			vis[sg[i-a[j]]]=1;
		}
		for(int j=0;j<1000;j++)//寻找不属于mex{}集合 ，且最小的 
		{
			if(vis[j]==0)
			{
				sg[i]=j;
				break;
			}
		}
	}
}