调节作用分析全解析：理论与SPSSAU实践指南

在科研与管理研究中，我们常常发现：相同的自变量，对因变量的影响并不是固定的。为什么在某些环境下关系更强，而在另一些情况下却减弱甚至消失？这背后，往往隐藏着一个被称为 “调节变量（Moderator）” 的机制。

一、从“影响”到“被影响的影响”：调节效应的理论内涵

调节效应（Moderation Effect） 描述的是：自变量 X 对因变量 Y 的影响，会随着某个第三变量 Z 的水平变化而发生改变。换句话说，调节变量不是直接产生结果，而是影响“影响”本身。在统计语言中，这种机制通过“交互项（interaction term）”被捕捉到。

举个直觉性的例子：

• 当“领导管理（Z）”水平较高时，“工作回报（X）”对“创新绩效（Y）”的影响可能更强；
• 当“领导管理（Z）”水平较低时，这种影响可能减弱。
  这种“因环境或条件而异”的关系，就是典型的调节效应。

二、SPSSAU 调节效应的整体分析逻辑

在 SPSSAU 中，调节效应分析遵循经典的 多层回归模型逻辑。系统通过三步（模型1、模型2、模型3）逐步引入变量，自动计算模型变化与显著性。

调节效应分析流程图：

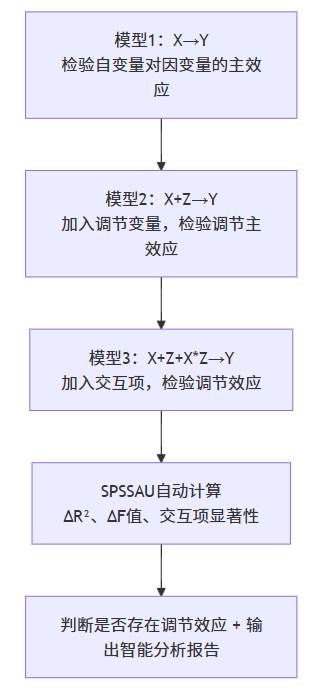
SPSSAU 会在后台自动完成三步回归，生成 ΔR²、ΔF、交互项显著性、斜率检验等全套结果。无需编写公式，也无需手动创建交互项，平台会在数据中心化或标准化处理后自动生成。

三、变量分类与数据处理逻辑

调节分析前，在调节作用分析开始前，适当的变量处理是确保结果准确性的关键。SPSSAU在此阶段提供了智能化的处理方案，可选择“调节类型”与“数据处理”方式。

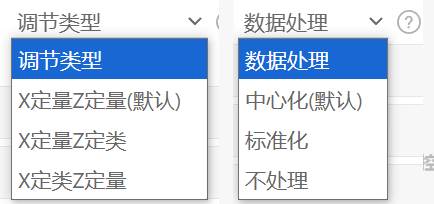
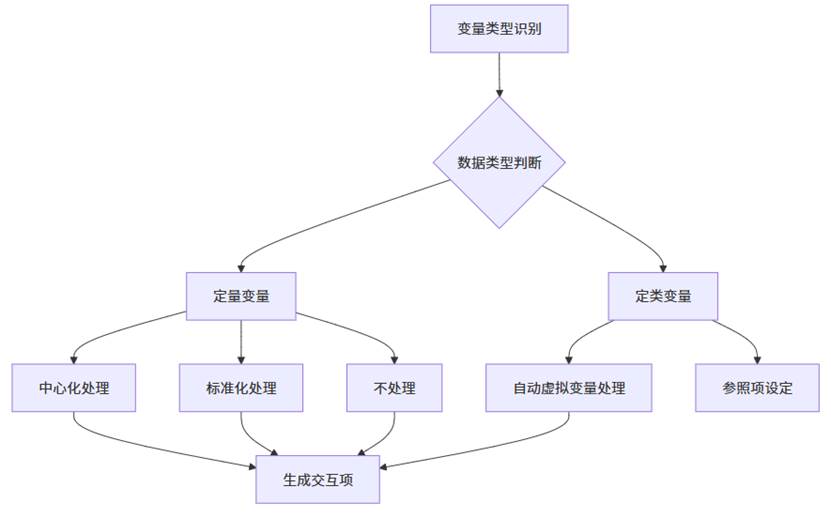
SPSSAU的智能化之处在于能够自动识别变量类型并推荐最合适的处理方式。对于定量变量，平台默认采用中心化处理，这有助于减少多重共线性问题，使得回归系数的解释更加直观。

举例说明如下：

变量类型	示例	处理方式	理论说明
因变量 (Y)	创新绩效	不处理	因变量是结果指标，不参与交互项生成。
自变量 (X)	工作回报	若为定量 → 中心化	减少多重共线性，使交互项解释更清晰。
调节变量 (Z)	领导管理	若为定量 → 中心化	便于解释主效应与交互效应。
控制变量	（若有）	直接放入模型	控制其对 Y 的直接影响，不影响交互项。

四、模型指标解读

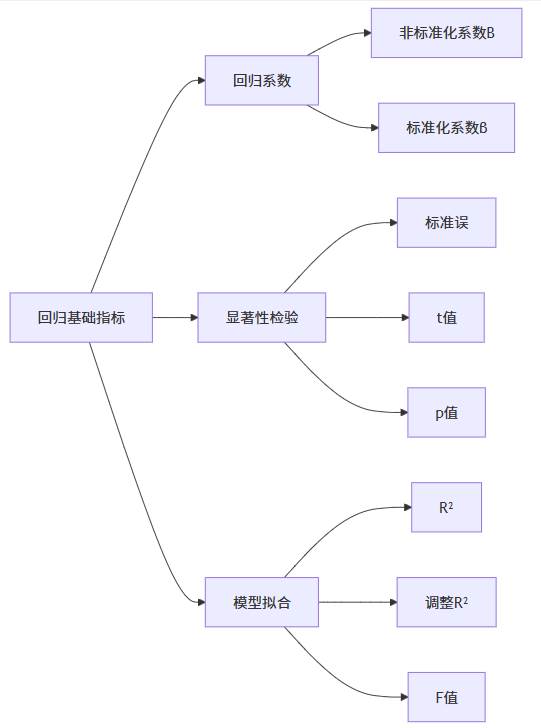
（1）回归模型基础指标

1. 回归系数的非标准化版本表示自变量每单位变化对因变量的实际影响大小，而标准化系数则消除了量纲影响，便于不同变量间的比较。
2. 显著性检验指标共同构成了统计推断的基础，其中p值提供了统计显著性的直接证据。
3. 模型拟合指标反映了模型对数据的解释力度，是评估模型质量的重要依据。

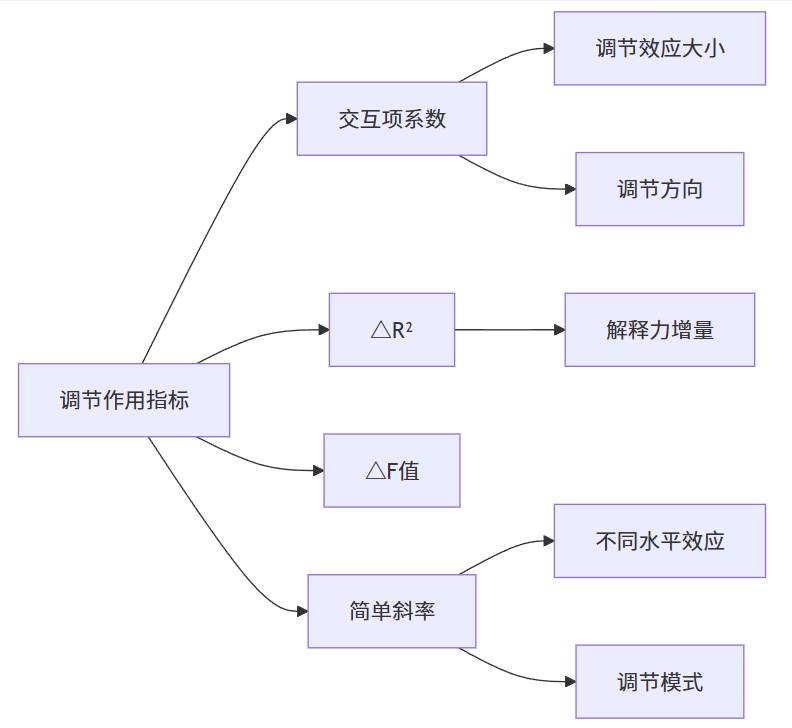
（2）调节作用专属指标

1. 交互项系数是调节作用的核心证据，反映了调节变量如何改变自变量与因变量之间的关系。
2. 模型比较指标（△R²和△F值）提供了调节效应的增量证据，表明加入交互项是否显著提升了模型的解释力。
3. 简单斜率分析在调节效应显著时进一步揭示调节作用的具体模式。

（3）置信区间指标

置信区间提供了参数估计的精度信息，是统计推断的重要组成部分。Bootstrap置信区间尤其适用于非正态分布或小样本情况。

（4）指标解释（理论层面）

指标	理论含义	说明
R²	模型解释度	表示模型可解释的总方差比例。越高说明拟合越好。
调整R²	修正解释度	考虑变量数影响，更公平比较不同模型。
F值	模型整体显著性	检验模型是否整体显著优于零模型。
ΔR²	解释度变化	判断新变量或交互项是否显著提升模型解释力。
ΔF	F值变化显著性	检验ΔR²的统计意义。
β（标准化回归系数）	路径强度	表征各变量的相对影响大小。
X*Z交互项	调节效应的核心指标	显著则说明 Z 改变了 X 对 Y 的影响斜率。

1. 若模型3中交互项显著，说明存在调节效应；
2. 若ΔR²显著提升，说明加入交互项后模型更优；
3. 若交互项不显著，则关系稳定，不受Z调节。

五、SPSSAU 智能输出中的逻辑判断路径

SPSSAU 不仅输出表格结果，还会给出系统化的结论判断。它的“智能分析模块”在后台使用逻辑树算法，结合显著性与ΔR²自动生成文字化解读。

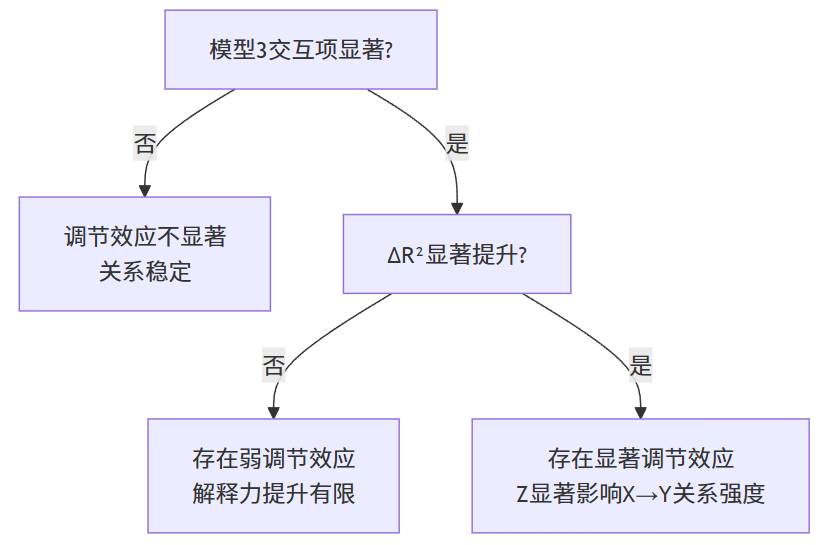SPSSAU 会在结果报告中自动描述：“交互项显著 → 存在调节效应”，“交互项不显著 → 调节作用不成立”，同时给出可视化解释图。

六、简单斜率分析

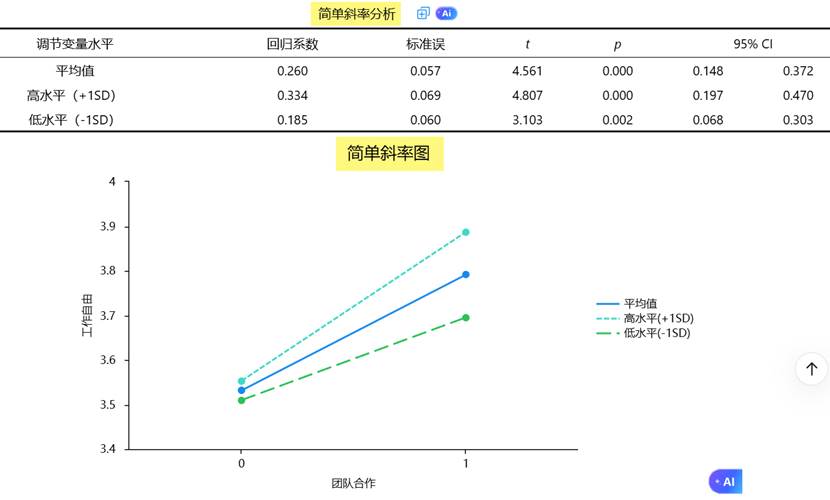
当调节效应显著时，SPSSAU 会进一步自动计算简单斜率（simple slope），即：在调节变量 Z 不同水平（高、低、均值）下，X 对 Y 的影响斜率差异。

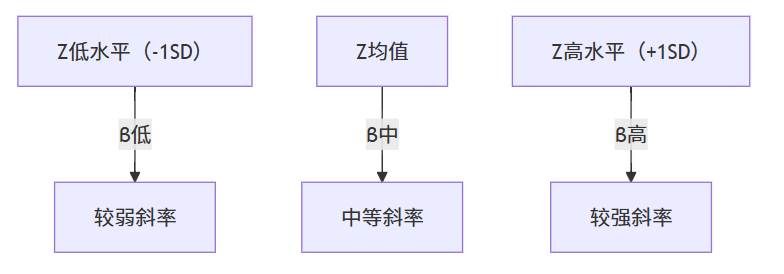
• 若三条斜率显著不同 → 调节效应成立；
• 若斜率差异不大 → 调节变量的“条件性影响”不明显。

SPSSAU 会自动生成“简单斜率表”与“斜率图”，帮助直观理解这种“随着Z变化而变化的X→Y关系”。

七、指标之间的逻辑链条：从路径到机制的全景视图

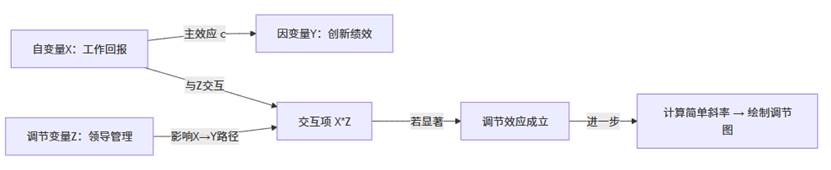
关联说明：

• 自变量 X 直接影响 Y；
• 调节变量 Z 改变了这一影响的强弱（体现“条件性”关系）；
• 交互项（X×Z）是理论与统计结合的关键桥梁；
• SPSSAU 通过交互项系数、ΔR²与简单斜率同时验证调节效应；
• 若均显著，则支持“Z在X→Y关系中起调节作用”的假设。

八、SPSSAU在调节作用分析中的技术优势

1. 智能化的变量处理系统：SPSSAU在变量处理方面展现出显著的技术优势：

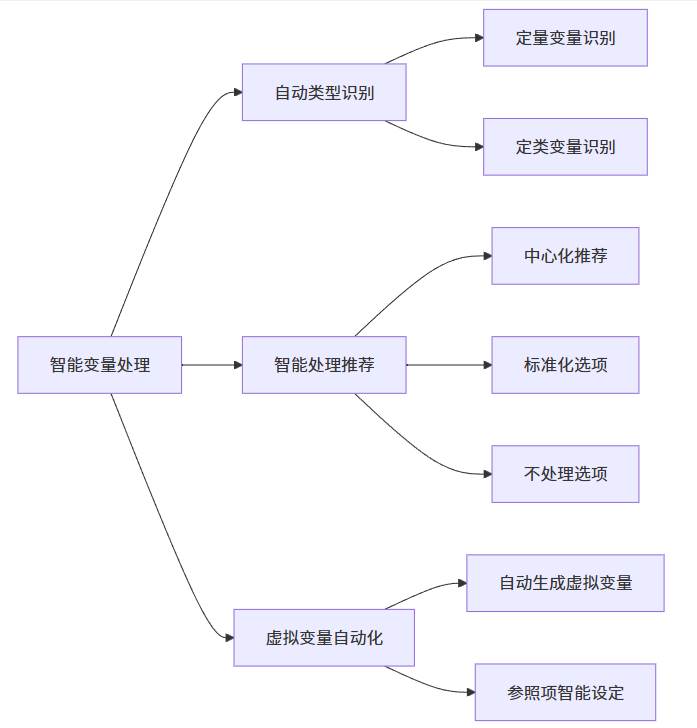
这种智能化处理不仅减少了用户的技术负担，也确保了分析方法的技术规范性。

2. 完整的调节检验流程

SPSSAU实现了调节作用检验的完整自动化：

• 自动模型构建：三个层次回归模型自动生成
• 智能效应检验：同时提供交互项显著性和模型比较证据
• 全面结果输出：从基础统计量到调节效应量的完整指标

3. 用户友好的结果解读

对于非统计背景的研究者，SPSSAU的"智能分析"功能提供了通俗易懂的结果解读，帮助用户理解复杂的统计结果背后的实际意义。

九、调节作用分析的方法学考量

1. 中心化与标准化的选择

在调节作用分析中，变量处理方式的选择需要基于研究目的：

中心化的优势：

• 减少多重共线性
• 提升系数的可解释性
• 特别适用于理论驱动的研究

标准化的适用场景：

• 变量量纲差异较大时
• 需要比较不同变量的相对效应时
• 跨研究比较时

SPSSAU提供多种处理选项，让研究者能够根据具体研究需求做出合适的选择。

2. 统计功效的考量

调节作用检测通常需要较大的样本量，因为交互项的检测功效往往低于主效应。SPSSAU在分析过程中会提供完整的样本信息，帮助研究者评估统计功效的充足性。

3. 简单斜率分析的深入应用

当调节效应显著时，简单斜率分析提供了深入理解调节模式的机会。SPSSAU自动提供调节变量在不同水平（均值、±1标准差）时的简单斜率估计，并配以图形化展示，极大便利了结果的解释和呈现。