差异性分析中效应量值计算与意义

在差异性分析中，效应量（Effect Size）是一个非常重要的指标，它用于衡量两组或多组数据之间的差异幅度。效应量不仅可以帮助我们判断差异是否显著，还可以量化差异的大小，从而为研究提供更深入的见解。以下是关于效应量的计算与意义的详细说明：

1. 效应量的定义

效应量是指在统计学中，用于衡量两组或多组数据之间差异大小的指标。它可以帮助我们理解差异的实际意义，而不仅仅是统计显著性。

2. 效应量的计算方法

不同的统计方法有不同的效应量计算方法。以下是几种常见统计方法的效应量计算方式：

2.1 T检验中的效应量

在T检验中，通常使用 Cohen's d值 来表示效应量。其计算公式为：

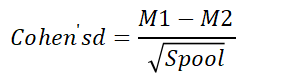
其中： - M1 和M2分别是两组数据的平均值。 

-  Spool是联合方差，计算公式为：

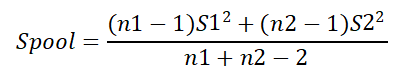
其中S1和S2分别是两组数据的标准差，n1和n2分别是两组数据的样本量。

2.2 方差分析中的效应量

在方差分析中，通常使用 Eta方 来表示效应量。其计算公式为：

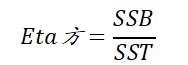
其中： SSB是组间差。SST是总差异。

2.3 卡方检验中的效应量

在卡方检验中，效应量的计算取决于数据的交叉类型。常见的效应量指标包括： 

- Phi：适用于2×2的交叉表。 

- 列联系数：适用于3×3或4×4的交叉表。 

- 校正列联系数：适用于n×n（n>4）的交叉表。 

- Cramer V：适用于m×n（m≠n）的交叉表。

3. 效应量的解释

效应量的大小通常有以下几种解释标准：

3.1 Cohen's d值的解释

• 0 < Cohen's d ≤ 0.2：效应较小（差异幅度较小）。
• 0.2 < Cohen's d ≤ 0.8：效应中等（差异幅度中等）。
• Cohen's d > 0.8：效应较大（差异幅度较大）。

3.2 Eta方的解释

• Eta方 < 0.01：效应较小。
• 0.01 ≤ Eta方 < 0.06：效应中等。
• Eta方 ≥ 0.14：效应较大。

4. 效应量的意义

效应量的意义在于它能够提供比P值更丰富的信息。P值只能告诉我们差异是否显著，而效应量则能够告诉我们差异的实际大小。这对于实际应用和决策制定非常重要。

5. 在SPSSAU中的操作

在SPSSAU(在线SPSS)中，进行差异性分析时，系统会自动计算并输出效应量。用户只需关注分析结果中的效应量指标，并根据上述标准进行解释即可。

6. 总结

效应量是差异性分析中不可或缺的一部分，它能够帮助我们更全面地理解数据之间的差异。通过计算和解释效应量，我们可以更好地评估研究结果的实际意义，并为后续的决策提供科学依据。