技术分享｜并行代数多重网格算法：如何用黑盒求解器攻克复杂工程计算的效率瓶颈？

一、多重网格方法介绍

多重网格方法是一种高效求解偏微分方程离散系统的迭代方法，其核心思想是通过不同网格层次的协同作用加速收敛。它分为几何多重网格（Geometric Multigrid Method, GMG）和代数多重网格（Algebraic Multigrid Method, AMG）两类，分别基于几何信息和纯代数结构构建。

传统迭代方法如雅可比(Jacobi)、高斯-赛德尔(Gauss–Seidel)方法虽能在细网格上快速消除高频误差，但对低频误差效果不佳。多重网格方法通过将问题转移到粗网格，使低频误差在粗网格上变为高频，从而被有效消除。它构建一系列从细到粗的网格，通过限制(Restriction)和插值(Interpolation, or Prolongation)在不同网格间传递信息，利用粗网格快速消除低频误差，细网格修正高频误差，以此加速收敛。

下图反映了一个2D泊松方程的迭代求解过程中残差分布的变化（初始随机分布），模型分辨率为100 × 100个网格点，使用的迭代方法为高斯-赛德尔迭代法。可以发现，长波长(低频)残差的衰减速度要比短波长(高频)残差慢得多。

图片来源：
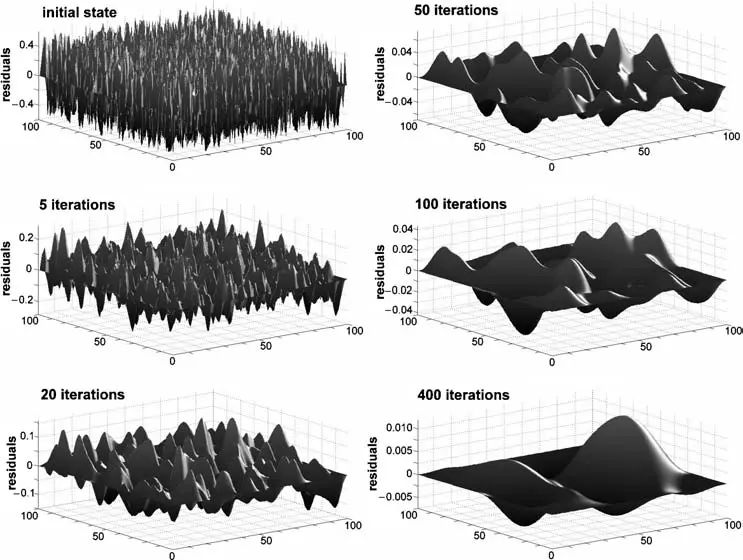
*Introduction to Numerical Geodynamic Modelling*

二、代数多重网格(AMG)方法

代数多重网格方法是一种用于求解稀疏线性方程组的高效数值计算方法，特别适用于工程和科学计算中的复杂问题。它通过将计算区域划分为多个层次化的网格，以提高计算效率和精度。AMG方法的基本思想是利用粗网格和细网格之间的关系，通过在不同层次上进行平滑和残差修正来加速求解过程。它结合了代数方法和多重网格技术，不需要显式的网格生成，而是直接在代数层面上操作，通过层次化拓扑关系的构建得到各层级的稀疏矩阵。这使得AMG方法具有较大的灵活性，可以适应不规则的几何形状和复杂的边界条件。

（一）主要特点

AMG与GMG的对比：

特性	几何多重网格（GMG）	代数多重网格（AMG）
依赖信息	几何网格结构	矩阵的代数结构
适用场景	结构化网格、规则问题	非结构化网格、复杂问题
粗网格构建	基于几何层次	基于矩阵的强连接性
插值/限制算子	基于几何插值（如线性插值）	基于矩阵的数值关系构造