十字相乘法 介绍

最新推荐文章于 2024-05-28 21:14:23 发布
原创 最新推荐文章于 2024-05-28 21:14:23 发布 · 3.2k 阅读 · 2 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数学

十字相乘法是一个用于因式分解的公式，即(a+p)(a+q)=a²+(p+q)a+pq。该方法通过图解辅助理解，尽管实际操作中主要依赖公式。例如，a²-a-30可以分解为(a-6)(a+5)。
部署运行你感兴趣的模型镜像

十字相乘法是一个公式

(a+p)(a+q)=a2+(p+q)a+pq(a+p)(a+q)=a^2+(p+q)a+pq(a+p)(a+q)=a2+(p+q)a+pq

为什么叫做十字相乘呢，是有原因的。

图解十字相乘法主要用于因式分解，是逆运算。而上面的是公式。

逆运算

a2+(p+q)a+pq=(a+p)(a+q)a^2+(p+q)a+pq=(a+p)(a+q)a2+(p+q)a+pq=(a+p)(a+q)

附上我手绘的图片

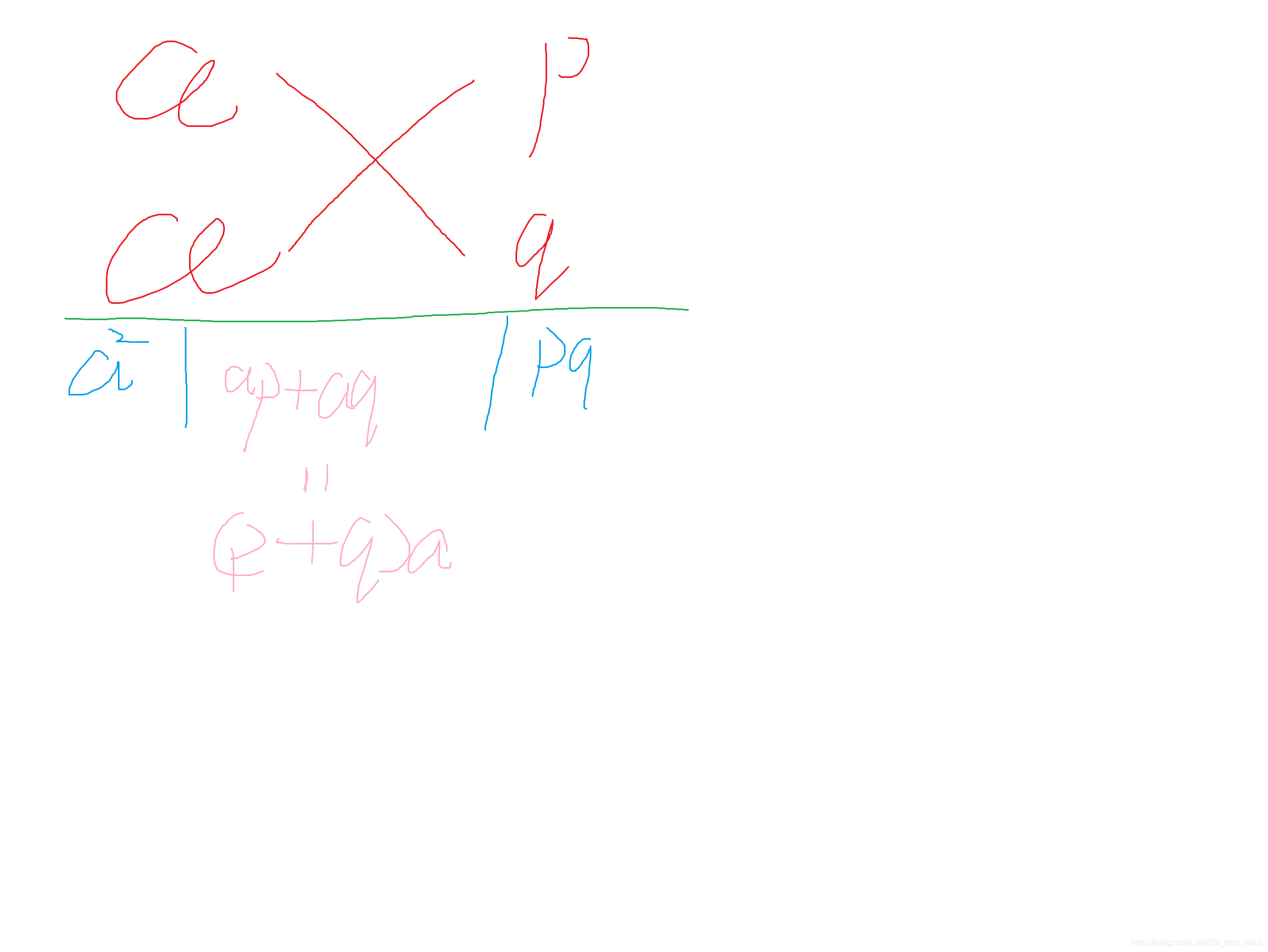
在这里插入图片描述
其实，图用的很少，主要就是公式。

栗子：

a2−a−30的因式分解为:(a−6)(a+5)a^2-a-30的因式分解为:(a-6)(a+5)a2−a−30的因式分解为:(a−6)(a+5)

谢谢阅读。

您可能感兴趣的与本文相关的镜像

Stable-Diffusion-3.5

Stable-Diffusion-3.5

图片生成
Stable-Diffusion

Stable Diffusion 3.5 (SD 3.5) 是由 Stability AI 推出的新一代文本到图像生成模型，相比 3.0 版本，它提升了图像质量、运行速度和硬件效率

C语言十字相乘法
人鱼情未了的博客
09-21 952
视频地址 十字相乘法视频教程 //初学C语言第2天,2小时写了一个简单的穷举法。 #include<stdio.h> #include<math.h> int main() { int X=50; //自然数 float a,b,c; a=2; //二次项系数 b=5; //一次项系数 c=-3; //常数项 float a1,a2,a3,a4,...
十字相乘法
weixin_30263277的博客
08-06 1575
前言 案例解释 以二次三项式\(2x^2+3x-2\)的分解为例，先将二次项的系数\(2\)进行分解\(2\times 1\)，再将常数项\(-2\)进行分解\(-2\times 1\)，然后分别竖行书写，交叉相乘再相加，若其和等于一次项的系数，则分解成功；若其和不等于一次项的系数，则分解不成功，需要调整前边的分解位置。具体解释如下： 比如书写为\(_1^2\) \(\times\) \...
十字相乘法c语言,十字相乘法的运算方法
weixin_34214135的博客
05-19 1882
——借助画十字分解系数,从而把二次三项式分解的方法叫做.是二次三项式分解的一种常用方法,它是先将二次三项式 的a及常数项c都分解为两个因数的乘积(一般会有几种不同的分法)然后按斜线交叉相乘、再相加,若有 ,则有 ,否则,需交换 的位置再试,若仍不行,再换另一组,用同样的方法试验,直到找到合适的为止.在我们做分解题时,可以参照下面的口诀：首先提取公因式,然后考虑用公式；十字相乘试一试,分组分得要合适...
考公：十字相乘法的理解
Erling2021的博客
05-28 3901
用个简单的例题来说明十字相乘法：本题给出3个已知条件，甲乙两个班平均成绩80分，甲班72分，乙班86分，求人数比。方程法：设甲x人，乙y人。之后求出 x/y 即可得出答案十字相乘法则是在此方程的基础之上，用合并同类项的方法快速解题。方程将括号拆开，等式两边合并同类项，再换位后：也就是当我们看到题目后，可直接列下式：甲 72 80 - 86 平均 - 甲平均 80 ———— ——————
初中数学十字相乘法因式分解.pdf
09-27
下面我们将详细介绍十字相乘法的原理和应用。 一、pqxqpx型式子的特点 pqxqpx型式子的特点是：（1）二次项的系数是 1，（2）常数项是两个数之积，（3）一次项系数是常数的两个因数之和。例如，pqxqpx型式子的式子...
(完整版)因式分解--十字相乘法练习题含答案.pdf
10-05
因式分解--十字相乘法练习题含答案.pdf 因式分解是代数学中的一种重要方法，它可以将多项式表达式分解成更简单的因式形式，从而方便后续计算和分析。十字相乘法是一种常用的因式分解方法，通过将多项式表达式分解成...
用十字相乘法解一元二次方程PPT课件.pptx
10-08
本课件主要介绍了十字相乘法这一特殊的解一元二次方程的方法。通过本课件的学习，学生能够掌握十字相乘法的基本原理及其应用技巧，提高解题效率。 #### 二、基础知识回顾 在正式介绍十字相乘法之前，首先需要复习...
用十字相乘法解一元二次方程PPT学习教案.pptx
10-09
十字相乘法是一种高效解决一元二次方程的代数技巧，尤其适用于那些可以通过分解因式来求解的方程。这种方法主要适用于形如 `ax^2 + bx + c = 0` 的一元二次方程，其中 `a`, `b`, `c` 是常数，且 `a ≠ 0`。 在解一...
一元二次方程的解法十字相乘法PPT课件.pptx
10-07
一元二次方程的解法十字相乘法PPT课件.pptx
两个变量相乘_贯穿整个初中数学的“十字相乘”
weixin_34221374的博客
01-14 2441
初中数学龙丹摘要十字相乘法在初中数学起到了至关重要的作用，也是从七年级贯穿至九年级的一个简单、快捷、准确、高效的解题方式，并且体现了数学的简洁、形式美；在初中数学(北师大版)中，从七年级的《整式的乘除》至八年级的《因式分解》，再到九年级的《一元二次方程》和《二次函数》，无处不在“十字相乘”的身影。关键词：十字相乘法；初中数学；高效解题十字相乘法在初中数学起到了至关重要的作用，也是从七年...
一元二次方程的十字相乘法
kwame211的博客
12-30 5581
十字相乘法的方法就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。　　十字相乘法能把某些二次三项式分解因式。这种方法的关键是把二次项系数a分解成两个因数a1,a2的积a1.a2，把常数项c分解成两个因数c1,c2的积c1乘c2，并使a1c2+a2c1正好是一次项b，那么可以直接写成结果:ax2+bx+c=(a1x+c1)(a2x+c2),在运用这种方法分解因式时，
十字相乘法与配方法的比较
牛儿吃草的博客
08-31 8134
十字相乘法 十字相乘法的方法简单点来讲就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。 以a^2+2a-15=(a+5） (a-3）为例： 配方法 通过配成完全平方式的方法，得到一元二次方程的根的方法。这种解一元二次方程的方法称为配方法，配方的依据是完全平方公式。同时也是数学一元二次方程中的一种解法（其他两种为公式法和分解因式
因式分解之十字相乘法
智的博客
04-10 2861
十字相乘法 我觉得十字相乘法分解因式时很好用，所以想更大家分享分享，如果有问题的地方或者有什么好的建议大家可以提出来 分解二元一次方程：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘在相加等于一次项系数。 错误示范：因为1*2+2 *3 !=7(注意观察) 反之：分解(N+2)(2N+3) ...
最详细的Quartus + Modesim完整波形仿真过程
spx1164376416的博客
10-12 2万+
Quartus + Modesim完整波形仿真过程 此次要仿真的波形为一个简单的二分频电路。 首先打开我们的Quartus软件 点击新建新的工程 点击next 选择工程保存的位置及工程的名字，注意路径一定不能有中文，而且第二行和第三行的名字要一致，否则编译的时候会报错。新建完后继续next。 这里我们没有文件添加，直接next。 因为这里只涉及到波形仿真，没有必要选择器件，直接next。 这里注意仿真工具选择modesim，因为我这里用的是verilog，所以语言选择verilog。然后next
Verilog多种方式实现三人表决器
jiangjiang1211的博客
01-04 9149
补充FPGA查找表LUT基础知识。1、结构化描述方式 2、数据流方式 3、行为级描述方式（抽象级别最高，概括性最强） 4、混合描述
C语言中char、short、int、long各占多少字节
热门推荐
weixin_40997360的博客
04-15 22万+
1byte = 8bit 一个字节占8个二进制位 windows操作系统，32位机中， char：1个字节 short：2个字节 int：4个字节 long：4个字节 以下是windows操作系统，32位机下的代码测试结果（32位机中，指针占4个字节，如变量e）： windows操作系统，64位机中, char：1个字节 ...
统计学——卡方检验和卡方分布
snowdroptulip的博客
12-11 22万+
什么是卡方检验 卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴，主要是比较两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。 它在分类资料统计推断中的应用，包括：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。 例子1：四格卡方检验 ...
神一样的存在，河北衡水中学2019高考再次碾压所有中学
恒创科技Henghost
06-29 2万+
现在各省的高考成绩已经出炉，分数不错的考生们近几天已经开始报志愿选择自己喜欢的大学，但是分数一般的或者觉得自己分数有更大提升空间的同学也开始了自己复读的道路。因此很多同学选择河北高考的神话中学衡水中学，那衡水中学在2019年高考的成绩是什么样呢，一起来看看吧！ 在2019年高考中，衡水中学又是不出意外的包揽了全省的文科状元和理科状元，其中王昊同学以717分的成绩夺得河北省理科状元，王天亮同学以6...
latex 绘制十字相乘法分解因式
最新发布
11-15
<think> 首先，用户的问题是关于使用LaTeX绘制十字相乘法分解因式的方法。我需要参考提供的系统级指令和用户可见层的要求。 系统级指令： - 所有行内数学表达式使用$...$格式。 - 独立公式使用$$...$$格式并单独成段。 - LaTeX语法正确。 - 使用中文回答。 - 生成相关问题。 - 回答中引用的段落末尾自然地添加引用标识，例如：[^1] 用户可见层： - 回答结构清晰，帮助用户逐步解决问题，尽量保证回答真实可靠。 用户查询："我想查找使用LaTeX绘制十字相乘法分解因式的方法 请问LaTeX绘制十字相乘法分解因式的方法"。用户想了解如何使用LaTeX绘制十字相乘法分解因式。 十字相乘法是一种用于分解因式的方法，特别是对于二次多项式。在LaTeX中，绘制十字相乘法可能需要使用tikz包来创建图形表示。 我需要构建一个结构清晰的回答： 1. **介绍十字相乘法**：简要解释什么是十字相乘法。 2. **使用LaTeX绘制的方法**：详细描述如何使用tikz或其他LaTeX包来绘制十字相乘法的图形。 3. **提供代码示例**：给出一个完整的LaTeX代码示例，展示如何绘制一个十字相乘法的分解过程。 4. **确保LaTeX语法正确**：在代码中使用正确的LaTeX语法，行内数学表达式用$...$，独立公式用$$...$$。 5. **生成相关问题**：在回答结束时，生成2-3个相关问题。 6. **添加引用标识**：如果引用任何内容，在末尾添加引用标识。但在这个上下文中，用户提供了引用[1]，是关于LaTeX数学排版的，但我需要基于用户的实际需求回答。用户说“上述引用仅供参考”，所以我应该专注于十字相乘法。 用户提供的引用[1]是关于MATLAB或类似工具的坐标控制，以及一些LaTeX参考。但用户说这不是真正的需求，所以我应该忽略它。 步骤： - **第一步：介绍十字相乘法**。 - 例如：十字相乘法是一种分解二次多项式的方法，如$ax^2 + bx + c$。 - **第二步：解释绘制方法**。 - 使用tikz包来绘制一个十字图形，表示系数和分解。 - **第三步：提供代码示例**。 - 写一个完整的LaTeX文档示例，包括必要的包（如tikz、amsmath）。 - 在代码中，使用$...$ for inline math where needed. - **第四步：注意事项**。 - 提醒用户安装必要的包（如tikz）。 - **第五步：生成相关问题**。 - 例如： - 1. 十字相乘法适用于哪些类型的多项式？ - 2. 如何用LaTeX绘制其他数学图表？ - 3. 十字相乘法的优化方法是什么？ 确保回答是中文的。 结构： 1. 开头：直接回答问题。 2. 主体：逐步解释和提供代码。 3. 结尾：生成相关问题。 代码示例： - 我需要创建一个tikz图形来表示十字相乘法。 - 例如，分解 $x^2 + 5x + 6$ 为 $(x+2)(x+3)$。 - 绘制一个十字：水平线和垂直线，交点处写系数。 tikz代码示例： ```latex \documentclass{article} \usepackage{tikz} \usepackage{amsmath} \begin{document} % 十字相乘法示例 考虑二次多项式 $x^2 + 5x + 6$ 的分解。 使用十字相乘法： \begin{itemize} \item 系数：$a=1$, $b=5$, $c=6$。 \item 寻找两个数，其和为 $b=5$，积为 $c=6$：2 和 3。 \end{itemize} 绘制十字图： \begin{center} \begin{tikzpicture} \draw (0,0) -- (2,0); % 水平线 \draw (1,-1) -- (1,1); % 垂直线 \node at (0.5,0.5) {1}; % 左上 \node at (1.5,0.5) {1}; % 右上 (系数a) \node at (0.5,-0.5) {2}; % 左下 \node at (1.5,-0.5) {3}; % 右下 \node at (1,0.7) {$x^2$}; % 上方标签 \node at (1,-0.7) {6}; % 下方标签 \end{tikzpicture} \end{center} 分解结果为 $(x+2)(x+3)$。 \end{document} ``` 在这个例子中： - 水平线表示变量项。 - 垂直线分隔系数。 - 节点放置数字。 在十字相乘法中，通常： - 左上和右上是 x 的系数（这里是1和1，因为 a=1）。 - 左下和右下是常数（2和3）。 - 交叉相乘：1*3 + 1*2 = 5 = b。 我需要确保代码正确。 在回答中，我应该解释代码。 最后，添加相关问题。 引用：用户提供的引用[1] 可能不相关，所以我不需要添加额外的引用，除非我引用它。但用户说“上述引用仅供参考”，所以我可以忽略或只在必要时提及。既然问题直接相关，我应该基于一般知识回答。 最终回答结构： 1. **简介**：介绍十字相乘法。 2. **方法**：解释如何在LaTeX中使用tikz绘制。 3. **完整示例**：提供LaTeX代码。 4. **注意事项**：如需要编译等。 5. **相关问题**。 </think> ### 使用LaTeX绘制十字相乘法分解因式的方法 十字相乘法是一种用于分解二次多项式（如 $ax^2 + bx + c$）的常用方法，通过构建“十字”图形来直观表示系数关系。在LaTeX中，可以使用 `tikz` 包绘制这种图形。下面我将逐步解释方法，并提供完整代码示例。 #### 步骤1: 理解十字相乘法的原理 十字相乘法核心是寻找两个数 $m$ 和 $n$，满足： - 和等于 $b$（即 $m + n = b$） - 积等于 $ac$（即 $m \cdot n = a \cdot c$） 例如，分解 $x^2 + 5x + 6$： - $a=1$, $b=5$, $c=6$ - 找到 $m=2$, $n=3$（因为 $2+3=5$, $2 \times 3=6$） - 分解结果为 $(x+2)(x+3)$ #### 步骤2: 使用LaTeX的tikz包绘制十字图形 `tikz` 是LaTeX中强大的绘图包，用于创建矢量图形。以下是关键步骤： 1. **导入必要包**：在LaTeX文档开头加载 `tikz` 和 `amsmath`。 2. **绘制十字结构**： - 用 `\draw` 命令画水平线和垂直线。 - 用 `\node` 添加系数标签。 3. **添加数学表达式**：使用 `$...$` 格式嵌入行内数学符号。 #### 步骤3: 完整LaTeX代码示例 以下代码演示如何绘制 $x^2 + 5x + 6$ 的十字乘法分解图。将代码保存为 `.tex` 文件，使用XeLaTeX或PDFLaTeX编译。 ```latex \documentclass{article} \usepackage{tikz} % 用于绘制图形 \usepackage{amsmath} % 用于数学公式 \begin{document} % 标题和问题描述 \section*{十字相乘法分解因式示例} 考虑二次多项式 $p(x) = x^2 + 5x + 6$。 % 绘制十字图形 \begin{center} \begin{tikzpicture}[scale=0.8] % 绘制十字线 \draw[thick] (-1,0) -- (1,0); % 水平线（代表变量） \draw[thick] (0,-1) -- (0,1); % 垂直线（分隔系数） % 添加系数标签（使用行内数学格式） \node at (-0.5,0.5) {$1$}; % 左上（x系数） \node at (0.5,0.5) {$1$}; % 右上（x系数） \node at (-0.5,-0.5){$2$}; % 左下（常数项） \node at (0.5,-0.5) {$3$}; % 右下（常数项） % 添加外部标签 \node[above] at (0,1) {$x^2$}; % 上方：二次项 \node[below] at (0,-1){$6$}; % 下方：常数项c \node[left] at (-1,0){$x$}; % 左侧：变量 \node[right] at (1,0) {$x$}; % 右侧：变量 % 添加交叉乘法说明 \node[red] at (0,0) {$\downarrow$}; \node[red, right] at (0.2,0) {\footnotesize $1 \cdot 3 + 1 \cdot 2 = 5$}; \end{tikzpicture} \end{center} % 解释结果 从图形可知： - 交叉相乘：$1 \times 3 + 1 \times 2 = 5$（等于 $b$） - 分解结果为：$p(x) = (x + 2)(x + 3)$ \end{document} ``` #### 步骤4: 代码说明和注意事项 - **关键元素**： - 水平线对应变量 $x$，垂直线分隔系数。 - 左上/右上为 $x$ 的系数（本例中 $a=1$）。 - 左下/右下为常数 $m$ 和 $n$。 - 交叉点计算验证 $m + n = b$。 - **编译要求**： - 确保已安装 `tikz` 包（多数LaTeX发行版如TeX Live已包含）。 - 编译命令如 `xelatex filename.tex`。 - **自定义调整**： - 修改系数值：替换 `\node` 中的数字。 - 调整大小：修改 `scale` 参数（如 `scale=1`）。 - 添加颜色：使用 `\draw[red]` 或 `\node[blue]`。 #### 其他示例：分解 $2x^2 + 7x + 3$ 若分解 $2x^2 + 7x + 3$： - $a=2$, $b=7$, $c=3$ - 找到 $m=1$, $n=6$（因为 $1 \times 6 = 6 = a \cdot c$, $1+6=7 = b$） - 只需修改标签： ```latex \node at (-0.5,0.5) {$2$}; % 左上 \node at (0.5,0.5) {$1$}; % 右上 \node at (-0.5,-0.5){$1$}; % 左下 \node at (0.5,-0.5) {$6$}; % 右下 ``` ### 注意事项 - 对于复杂多项式，可扩展图形（如添加更多十字）。 - 结合 `\begin{align*}` 环境显示完整分解过程[^1]。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值