5.3 B 样条曲线与曲面
B 样条曲线方程的定义
Bezier曲线的不足:阶次较大时特征多边形对曲线的控制将会减弱;没有局部性、不能做局部修改;拼接较复杂
B 样条曲线方程: P(t)=∑i=0nPiNi,k(t)P(t)=\sum\limits_{i=0}^nP_iN_{i,k}(t)P(t)=i=0∑nPiNi,k(t) ,其中:
- Pi (i=0,1,...,n)P_i\,(i=0,1,...,n)Pi(i=0,1,...,n) 是控制多边形的顶点
- 给定参数 ttt 轴上的一个分割 T={ti: t0≤ti≤...≤tn+k}T=\{t_i:\,t_0\le t_i\le...\le t_{n+k}\}T={ti:t0≤ti≤...≤tn+k} ,TTT 称为节点矢量
- Ni,k(t)N_{i,k}(t)Ni,k(t) 称为 TTT 的 kkk 阶 B 样条基函数(调和函数),是一个 kkk 阶( k−1k-1k−1 次)分段多项式样条。其中每一个称为 B 样条,定义为:
Ni,1(t)={1ti≤x≤ti+10elseNi,k(t)=t−titi+k−1−tiNi,k−1(t)+ti+k−tti+k−ti+1Ni+1,k−1(t) N_{i,1}(t)= \left\{ \begin{array}{ll} 1 & t_i\le x\le t_{i+1} \\ 0 & else \end{array} \right. \\ N_{i,k}(t)=\frac{t-t_i}{t_{i+k-1}-t_i}N_{i,k-1}(t)+\frac{t_{i+k}-t}{t_{i+k}-t_{i+1}}N_{i+1,k-1}(t) Ni,1(t)={10ti≤x≤ti+1elseNi,k(t)=ti+k−1−tit−tiNi,k−1(t)+ti+k−ti+1ti+k−tNi+1,k−1(t)
欲确定第 iii 个 kkk 阶 B 样条 Ni,k(t)N_{i,k}(t)Ni,k(t) ,需要用到 ti,ti+1,...,ti+kt_i,t_{i+1},...,t_{i+k}ti,ti+1,...,ti+k 共 k+1k+1k+1 个节点,称区间 [ti,ti+k][t_i, t_{i+k}][ti,ti+k] 为 Ni,k(t)N_{i,k}(t)Ni,k(t) 的支撑区间;
曲线方程中,n+1n+1n+1 个控制顶点 Pi (i=0,1,...,n)P_i\,(i=0,1,...,n)Pi(i=0,1,...,n) ,要用到 n+1n+1n+1 个 kkk 阶B样条 Ni,k(t)N_{i,k}(t)Ni,k(t) ,它们支撑区间的并集定义了这一组B样条基的节点矢量 T=[t0,t1,...,tn+k]T=[t_0,t_1,...,t_{n+k}]T=[t0,t1,...,tn+k] ;
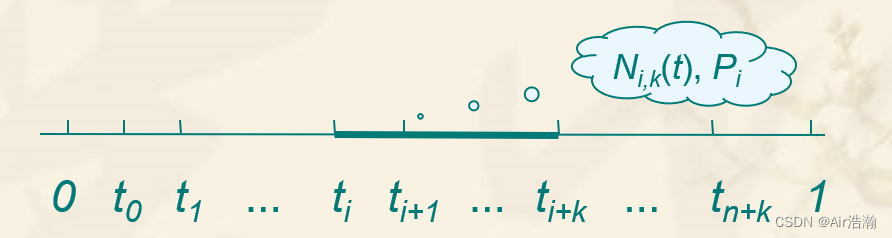
B 样条基函数的性质
局部支撑性是最重要的性质
局部支撑性: Ni,k(t)={≥0t∈[ti,ti+k]=0elseN_{i,k}(t)=\left\{\begin{array}{ll}\ge0 & t\in[t_i,t_{i+k}] \\=0 & else \end{array}\right.Ni,k(t)={≥0=0t∈[ti,ti+k]else
权性: ∑i=0nNi,k(t)=1\sum\limits_{i=0}^nN_{i,k}(t)=1i=0∑nNi,k(t)=1 ,t∈[tk−1,tn+1]t\in[t_{k-1},t_{n+1}]t∈[tk−1,tn+1]
微分公式: Ni,k′(t)=k−1ti+k−1−tiNi,k−1(t)−k−1ti+k−ti+1Ni+1,k−1(t)N'_{i,k}(t)=\frac{k-1}{t_{i+k-1}-t_i}N_{i,k-1}(t)-\frac{k-1}{t_{i+k}-t_{i+1}}N_{i+1,k-1}(t)Ni,k′(t)=ti+k−1−tik−1Ni,k−1(t)−ti+k−ti+1k−1Ni+1,k−1(t)
次数:
- Ni,k(t)N_{i,k}(t)Ni,k(t) 在每一段 [ti, ti+k][t_i,\,t_{i+k}][ti,ti+k] 上都是次数不高于 k−1k-1k−1 的多项式
- Ni,k(t)N_{i,k}(t)Ni,k(t) 在 lll 重结点处的连续阶不低于 k−1−lk-1-lk−1−l 阶:ti−1<ti=ti+1=...=ti+l−1<ti+lt_{i-1}\lt t_i=t_{i+1}=...=t_{i+l-1}\lt t_{i+l}ti−1<ti=ti+1=...=ti+l−1<ti+l
B 样条曲线的类型划分
① 按照首末端点是否重合,分为闭曲线和开曲线;闭曲线又区分为周期和非周期两种情形:
- 周期闭曲线在首末端点是 C2C^2C2 连续的,而非周期闭曲线一般是 C0C^0C0 连续的
- 非周期闭曲线可以认为是开曲线的特例,按开曲线处理
② 按照节点矢量中节点的分布情况,分为四种类型:
- 均匀 B 样条曲线:节点矢量中节点沿参数轴均匀或等距分布
- 准均匀 B 样条曲线:与均匀 B 样条曲线差别在于两端节点具有重复度 k
- 分段 Bezier 曲线:节点矢量中,两端点节点具有重复度 k,所有内节点重复度为 k - 1
- 非均匀 B 样条曲线:节点矢量中的节点任意分布
(重复度就是指节点矢量中连续相等的节点数,比如某段区间有 tj−1<tj=tj+1=...=tj+l−1<tj+lt_{j-1}\lt t_j=t_{j+1}=...=t_{j+l-1}\lt t_{j+l}tj−1<tj=tj+1=...=tj+l−1<tj+l ,则中间相等的节点称为 TTT 的 lll 重节点 )
B 样条曲线的性质
局部性是最重要的性质,要记住下标
局部性:
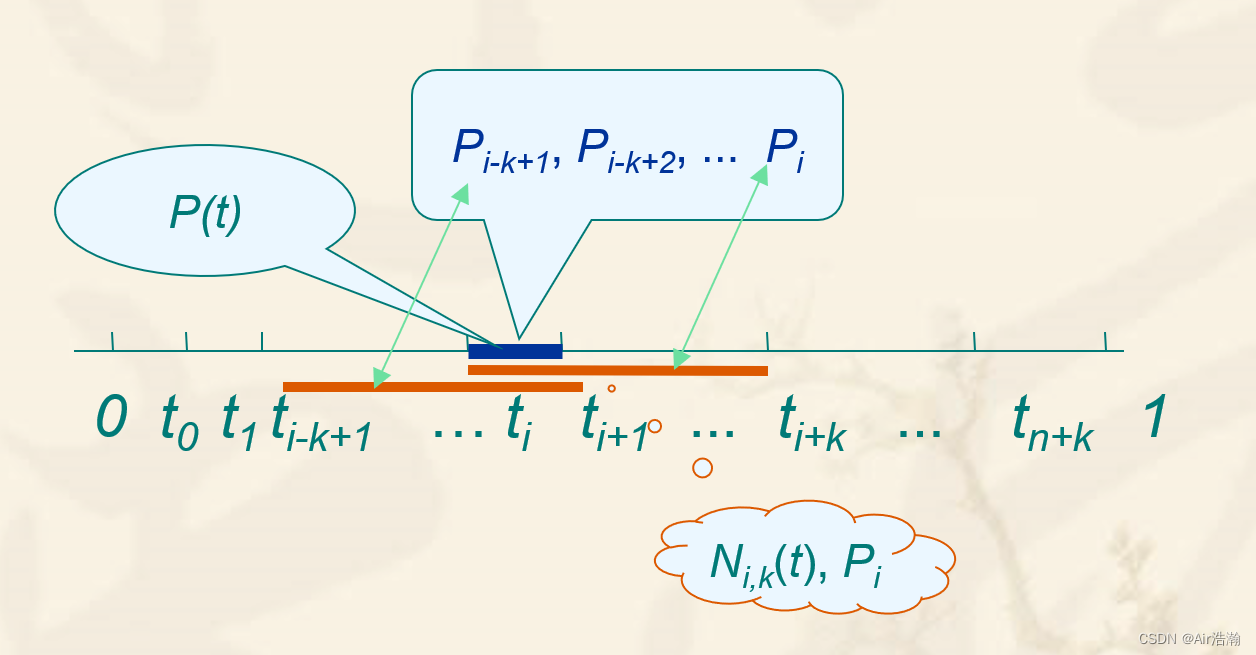
- B 样条曲线上参数为 t∈[ti, ti+1]t\in[t_i,\,t_{i+1}]t∈[ti,ti+1] 的点 P(t)P(t)P(t) 至多与 kkk 个控制顶点 Pj (i−k+1,...,i)P_j\,(i-k+1,...,i)Pj(i−k+1,...,i) 有关,而与其他控制顶点无关;
- 移动点该曲线第 iii 个控制顶点 PiP_iPi 至多影响到定义在区间 (ti, ti+k)(t_i,\,t_{i+k})(ti,ti+k) 上(即 Ni,k(t)N_{i,k}(t)Ni,k(t) 支撑区间上)那部分曲线的形状,对曲线其余部分不发生影响
连续性:
分段参数多项式、导数公式:
凸包性、变差缩减性、几何不变性、仿射不变性: 与 Bezier 曲线相同
直线保持性: 控制顶点形成一条直线时,构成的 B 样条曲线也是一条直线
造型灵活性: 可以构造直线段、尖点、切线、过定点等特殊情况
B 样条曲线的矩阵表示
(这里只研究一次、二次和三次的均匀 B 样条曲线的矩阵表示;一次没有考过,都是考二次和三次;给出矩阵,写出代数形式,然后推导一阶、二阶的位置矢量和导数矢量,可能会画图)
一次 B 样条曲线
每相邻两个点可构造出一段一次 B 样条曲线

二次 B 样条曲线
每相邻三个点可构造出一段一次 B 样条曲线

三次 B 样条曲线
每相邻四个点可构造出一段一次 B 样条曲线


de Boor 算法
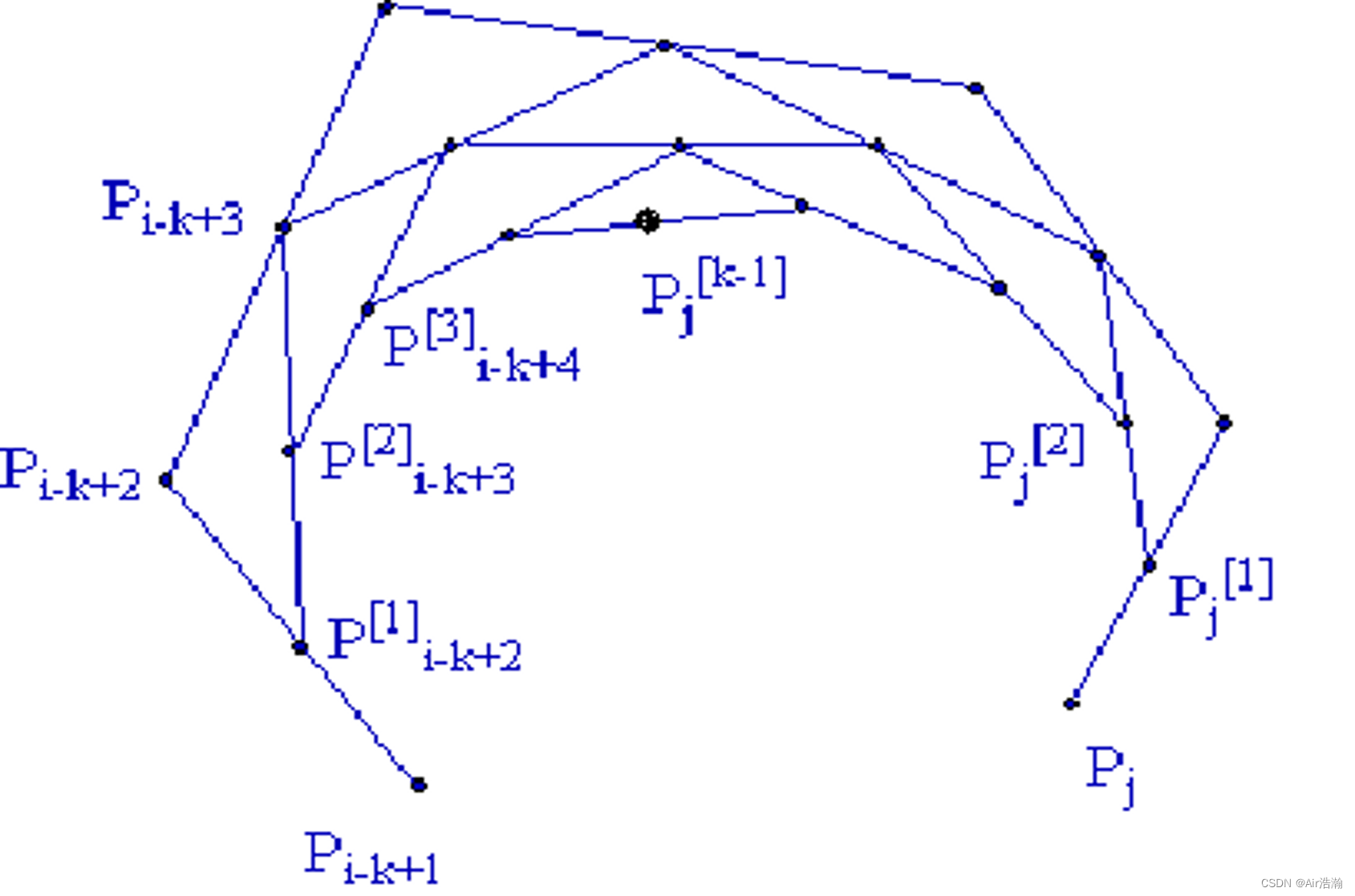
写出顶点的递推关系;注意下标;只需要画示意图,不需要精确作图
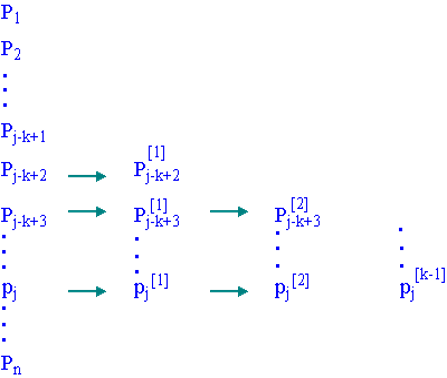
类似于 Bezier 曲线的 de Casteljau 算法,不用带入方程去求出曲线上的某一点,而是采用递归的方式求出:
Pi[r](t)={Pir=0, i=j−k+1,...,jt−titi+k−r−tiPi[r−1](t)+ti+k−r−tti+k−r−tiPi−1[r−1](t)elser=1,2,...,k−1;i=j−k+r+1,...,j
P_i^{[r]}(t)=
\left\{
\begin{array}{ll}
P_i & r=0,\,i=j-k+1,...,j \\
\frac{t-t_i}{t_{i+k-r}-t_i}P_i^{[r-1]}(t)+\frac{t_{i+k-r}-t}{t_{i+k-r}-t_i}P_{i-1}^{[r-1]}(t) & else
\end{array}
\right. \\\\
r=1,2,...,k-1;\quad i=j-k+r+1,...,j
Pi[r](t)={Piti+k−r−tit−tiPi[r−1](t)+ti+k−r−titi+k−r−tPi−1[r−1](t)r=0,i=j−k+1,...,jelser=1,2,...,k−1;i=j−k+r+1,...,j
最终迭代 kkk 次,得到 P(t)=Pj[k−1](t)P(t)=P_j^{[k-1]}(t)P(t)=Pj[k−1](t)
节点插入算法
一般不会考的
B 样条曲面
一般不会考的
5.4 NURBS曲线与曲面
NURBS 曲线的定义
记住NURBS的全称
NURBS(non-uniform rational B-spline):非均匀有理 B 样条方法
(有理曲线就是,比如在平面上用参数方程表示曲线时,x(t)x(t)x(t) 和 y(t)y(t)y(t) 都是有理函数)
优点: NURBS 既与描述自由型曲线、曲面形状的 B 样条方法相统一,又能精确表示二次胡与二次曲面(初等曲线、曲面)
定义: NURBS 曲线是由分段有理 B 样条多项式基函数定义的,给每个控制顶点加上了加上了权重因子(在 B 样条的基础上增加了一个吸引力权重,权重反映了控制顶点对曲线的吸引程度):
P(t)=∑i=0nωiPiNi,k(t)∑j=0nωjNj,k(t)=∑i=0nPiRi,k(t)Ri,k=ωiNi,k(t)∑j=0nωjNj,k(t)
P(t)=\frac{\sum\limits_{i=0}^n\omega_iP_iN_{i,k}(t)}{\sum\limits_{j=0}^n\omega_jN_{j,k}(t)}=\sum\limits_{i=0}^nP_iR_{i,k}(t)
\quad\quad\quad
R_{i,k}=\frac{\omega_iN_{i,k}(t)}{\sum\limits_{j=0}^n\omega_jN_{j,k}(t)}
P(t)=j=0∑nωjNj,k(t)i=0∑nωiPiNi,k(t)=i=0∑nPiRi,k(t)Ri,k=j=0∑nωjNj,k(t)ωiNi,k(t)
Ri,k(t) (i=0,...,n)R_{i,k}(t)\,(i=0,...,n)Ri,k(t)(i=0,...,n) 称为 kkk 阶有理基函数
NURBS 曲线的性质
最重要的还是局部性
① NURBS 基函数的性质:
局部支撑性: Ri,k(t)=0,t∉[ti, ti+k]R_{i,k}(t)=0,\quad t\notin[t_i,\,t_{i+k}]Ri,k(t)=0,t∈/[ti,ti+k]
权性: ∑i=0nRi, k(u)=1\sum\limits_{i=0}^nR_{i,\,k}(u)=1i=0∑nRi,k(u)=1
可微性: 若分母不为零,
- 在节点区间内无限次连续可微;
- 在节点处 (k−1−r)(k-1-r)(k−1−r) 次连续可微, rrr 是该节点的重复度;
② NURBS 曲线的性质:
局部性质:
- kkk 阶 NURBS 曲线上参数为 t∈[ti, ti+k]⊂[tk−1, tn+1]t\in[t_i,\,t_{i+k}]\sub[t_{k-1},\,t_{n+1}]t∈[ti,ti+k]⊂[tk−1,tn+1] 的一点 P(t)P(t)P(t) 至多与 kkk 个控制顶点 PjP_jPj 及权因子 ωj (j=i−k+1,...,i)\omega_j\,(j=i-k+1,...,i)ωj(j=i−k+1,...,i) 有关,与其他顶点和权因子无关;
- 若移动 kkk 次 NURBS 曲线的一个控制顶点 PiP_iPi 或改变其对应的权因子 ωi\omega_iωi ,则仅仅影响定义在区间 [ti, ti+k]⊂[tk−1, tn+1][t_i,\,t_{i+k}]\sub[t_{k-1},\,t_{n+1}][ti,ti+k]⊂[tk−1,tn+1] 那部分曲线的形状
变差缩减性、凸包性、仿射与透射变换不变性: 与 Bezier 曲线相同
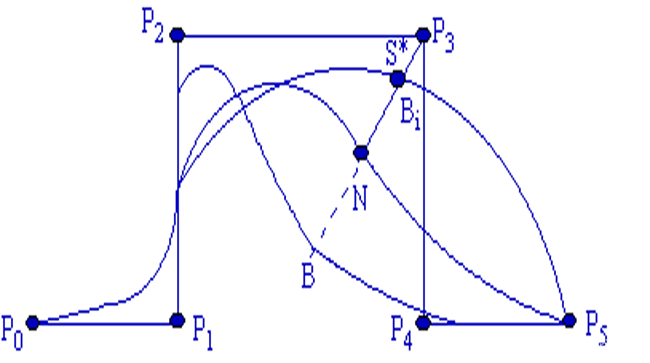
权因子的几何意义
要记住形状因子和权因子对曲线的影响表现在图上的样子
记 BBB 、NNN 、BiB_iBi 分别为 ωi=0\omega_i=0ωi=0 、ωi=1\omega_i=1ωi=1 和 ωi≠0, 1\omega_i\not=0,\,1ωi=0,1 对应曲线上的点,即:B=P(t; ωi=0)B=P(t;\,\omega_i=0)B=P(t;ωi=0) ,N=P(t; ωi=1)N=P(t;\,\omega_i=1)N=P(t;ωi=1) ,Bi=P(t; ωi≠0, 1)B_i=P(t;\,\omega_i\not=0,\,1)Bi=P(t;ωi=0,1) ,Pi=P(t; ωi→∞)P_i=P(t;\,\omega_i\to\infin)Pi=P(t;ωi→∞)
(BBB 代表 PiP_iPi 完全没有影响时曲线的形状;NNN 代表 PiP_iPi 的影响力和在 B 样条曲线中影响力一样时曲线的形状;BiB_iBi 代表在 B 样条曲线的基础上对 PiP_iPi 增加或减少影响力时曲线的形状)
令 α=Ri,k(t; ωi=1)\alpha=R_{i,k}(t;\,\omega_i=1)α=Ri,k(t;ωi=1) ,β=Ri,k(t)\beta=R_{i,k}(t)β=Ri,k(t) ,则:
N=(1−α)B+αPiBi=(1−β)B+βPiN−B=α(Pi−B)Bi−B=β(Pi−B)
N=(1-\alpha)B+\alpha P_i \quad\quad B_i=(1-\beta)B+\beta P_i \\
N-B=\alpha(P_i-B) \quad\quad B_i-B=\beta(P_i-B)
N=(1−α)B+αPiBi=(1−β)B+βPiN−B=α(Pi−B)Bi−B=β(Pi−B)
(Pi, Bi, N, B)(P_i,\,B_i,\,N,\,B)(Pi,Bi,N,B) 四点的交比为:
1−αα:1−ββ=PiNBN:PiBiBBi=ωi
\frac{1-\alpha}{\alpha}:\frac{1-\beta}{\beta}=\frac{P_iN}{BN}:\frac{P_iB_i}{BB_i}=\omega_i
α1−α:β1−β=BNPiN:BBiPiBi=ωi
- 若 ωi\omega_iωi 增大或减小,则 β\betaβ 页增大或减小,所以曲线被拉向或者推离开 PiP_iPi 点
- 若 ωi\omega_iωi 增大或减小,则曲线被推离开或者拉向 Pj (j≠i)P_j\,(j\not=i)Pj(j=i) 点
- 随着 BiB_iBi 的运动,它扫描出一条直线 BPiBP_iBPi
- 若 BiB_iBi 趋向 PiP_iPi ,则 β\betaβ 去向 1,ωj\omega_jωj 趋向正无穷
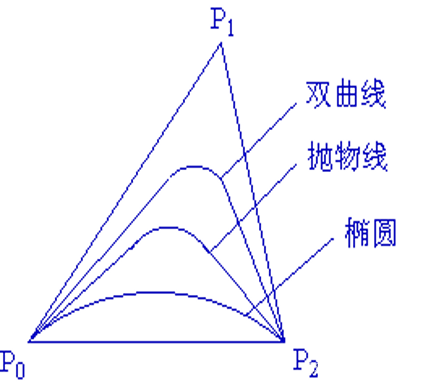
圆锥曲线的 NURBS 表示
取节点向量为 T=[0,0,0,1,1,1]T=[0,0,0,1,1,1]T=[0,0,0,1,1,1] ,则 NURBS 曲线退化为二次 Bezier 曲线,可以证明这是圆锥曲线弧方程:
P(t)=(1−t2)ω0P0+2t(1−t)ω1P1+t2ω2P2(1−t2)ω0+2t(1−t)ω1+t2ω2
P(t)=\frac{(1-t^2)\omega_0P_0+2t(1-t)\omega_1P_1+t^2\omega_2P_2}{(1-t^2)\omega_0+2t(1-t)\omega_1+t^2\omega_2}
P(t)=(1−t2)ω0+2t(1−t)ω1+t2ω2(1−t2)ω0P0+2t(1−t)ω1P1+t2ω2P2
形状因子: Csf=ω12ω0ω2Csf0(0, 1)1(1, +∞)→+∞曲线P0P2椭圆抛物线双曲线P0P1和P1P2C_{sf}=\frac{\omega_1^2}{\omega_0\omega_2} \quad\quad \begin{array}{|c|c|c|c|c|c|} \hline C_{sf} & 0 & (0,\,1) & 1 & (1,\,+\infin) & \to+\infin \\ \hline 曲线 & P_0P_2 & 椭圆 & 抛物线 & 双曲线 & P_0P_1和P_1P_2 \\ \hline \end{array}Csf=ω0ω2ω12Csf曲线0P0P2(0,1)椭圆1抛物线(1,+∞)双曲线→+∞P0P1和P1P2
NURBS曲线的修改
常用方法:修改权因子、修改控制点、反插节点
NURBS曲面
一般不会考的 注意这里权因子的下标变成了 ωij\omega_{ij}ωij
5.5 Coons曲面
Coons 曲面的定义
属于构造插值曲面的方法,用于构造通过给定型值点的曲面
基本概念: 假定参数曲面方程为 P(u, v) (u, v∈[0, 1])P(u,\,v)\,(u,\,v\in[0,\,1])P(u,v)(u,v∈[0,1])
- 曲面片的四条边界:P(u, 0)P(u,\,0)P(u,0) ,P(u, 1)P(u,\,1)P(u,1) ,P(0, v)P(0,\,v)P(0,v) ,P(1, v)P(1,\,v)P(1,v)
- 曲面片的四个角点:P(0, 0)P(0,\,0)P(0,0) ,P(0, 1)P(0,\,1)P(0,1) ,P(1, 0)P(1,\,0)P(1,0) ,P(1, 1)P(1,\,1)P(1,1)
要解决的问题: 给定四条在空间中围成封闭曲边四边形的参数曲线 P(u, 0)P(u,\,0)P(u,0) ,P(u, 1)P(u,\,1)P(u,1) ,P(0, v)P(0,\,v)P(0,v) ,P(1, v)P(1,\,v)P(1,v) ,构造一张参数曲面 P(u, v) (u, v∈[0, 1])P(u,\,v)\,(u,\,v\in[0,\,1])P(u,v)(u,v∈[0,1])

方法: 双线性 Coons 曲面和双三次 Coons 曲面
双线性 Coons 曲面
这些内容都要记住,给出图形,写出双线性构造的算法;双三次计算量较大,不太可能会考
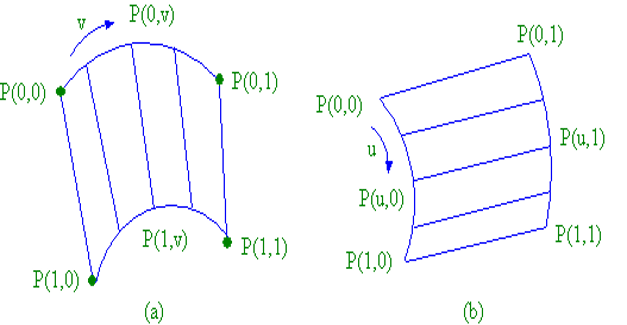
① 首先,在 uuu 向进行线性插值,得到以 P(0, v)P(0,\,v)P(0,v) 和P(1, v)P(1,\,v)P(1,v) 为边界的直纹面(如图 (b) ):
P1(u, v)=(1−u)P(0, v)+uP(1, v)
P_1(u,\,v)=(1-u)P(0,\,v)+uP(1,\,v)
P1(u,v)=(1−u)P(0,v)+uP(1,v)
② 接着,在 vvv 向进行线性插值,得到以 P(u, 0)P(u,\,0)P(u,0) 和P(u, 1)P(u,\,1)P(u,1) 为边界的直纹面(如图 (a) ):
P2(u, v)=(1−v)P(u, 0)+vP(u, 1)
P_2(u,\,v)=(1-v)P(u,\,0)+vP(u,\,1)
P2(u,v)=(1−v)P(u,0)+vP(u,1)
③ 再构造两条 vvv 向的连接端点的直线段:
(1−v)P(0, 0)+vP(0, 1)(1−v)P(1, 0)+vP(0, 1)
(1-v)P(0,\,0)+vP(0,\,1) \\
(1-v)P(1,\,0)+vP(0,\,1)
(1−v)P(0,0)+vP(0,1)(1−v)P(1,0)+vP(0,1)
以这两条直线段为边界,构造直纹面 P3(u, v)P_3(u,\,v)P3(u,v) :
P3(u, v)=(1−u)[(1−v)P(0, 0)+vP(0, 0)]+u[(1−v)P(1, 0)+vP(1, 1)]=[1−uu][P(0,0)P(0,1)P(1,0)P(1,1)][1−vv]u, v∈[0, 1]
P_3(u,\,v)=(1-u)[(1-v)P(0,\,0)+vP(0,\,0)]+u[(1-v)P(1,\,0)+vP(1,\,1)] \\=
\begin{bmatrix}
1-u & u
\end{bmatrix}
\begin{bmatrix}
P(0,0) & P(0,1) \\
P(1,0) & P(1,1)
\end{bmatrix}
\begin{bmatrix}
1-v \\
v
\end{bmatrix}
\quad\quad u,\,v\in[0,\,1]
P3(u,v)=(1−u)[(1−v)P(0,0)+vP(0,0)]+u[(1−v)P(1,0)+vP(1,1)]=[1−uu][P(0,0)P(1,0)P(0,1)P(1,1)][1−vv]u,v∈[0,1]
④ P(u, v)=P1(u, v)+P2(u, v)−P3(u, v)P(u,\,v)=P_1(u,\,v)+P_2(u,\,v)-P_3(u,\,v)P(u,v)=P1(u,v)+P2(u,v)−P3(u,v) 便是所要构造的面,矩阵形式为:
P(u, v)=−[−11−uu][0P(u,0)P(u,1)P(0,v)P(0,0)P(0,1)P(1,v)P(1,0)P(1,1)][−11−vv]u, v∈[0, 1]
P(u,\,v)= -
\begin{bmatrix}
-1 & 1-u & u
\end{bmatrix}
\begin{bmatrix}
0 & P(u,0) & P(u,1) \\
P(0,v) & P(0,0) & P(0,1) \\
P(1,v) & P(1,0) & P(1,1)
\end{bmatrix}
\begin{bmatrix}
-1 \\
1-v \\
v
\end{bmatrix}
\quad\quad u,\,v\in[0,\,1]
P(u,v)=−[−11−uu]⎣⎡0P(0,v)P(1,v)P(u,0)P(0,0)P(1,0)P(u,1)P(0,1)P(1,1)⎦⎤⎣⎡−11−vv⎦⎤u,v∈[0,1]
双三次 Coons 曲面
建议直接背诵[流汗]
① 使用 Hermite 基函数 F0F_0F0 、F1F_1F1 、G0G_0G0 和 G1G_1G1 作为调和函数,构造 uuu 向和 vvv 向的曲面:
P1(u, v)=F0(u)P(0, v)+F1(u)P(1, v)+G0(u)Pu(0, v)+G1(u)Pu(1, v)P2(u, v)=F0(v)P(u, 0)+F1(v)P(u, 1)+G0(v)Pv(u, 0)+G1(v)Pv(u, 1)
P_1(u,\,v)=F_0(u)P(0,\,v)+F_1(u)P(1,\,v)+G_0(u)P_u(0,\,v)+G_1(u)P_u(1,\,v) \\
P_2(u,\,v)=F_0(v)P(u,\,0)+F_1(v)P(u,\,1)+G_0(v)P_v(u,\,0)+G_1(v)P_v(u,\,1) \\
P1(u,v)=F0(u)P(0,v)+F1(u)P(1,v)+G0(u)Pu(0,v)+G1(u)Pu(1,v)P2(u,v)=F0(v)P(u,0)+F1(v)P(u,1)+G0(v)Pv(u,0)+G1(v)Pv(u,1)
PuP_uPu 、PvP_vPv 指切矢量,u, v∈[0, 1]u,\,v\in[0,\,1]u,v∈[0,1]
② 对角点的数据进行插值,可得曲面 P3(u, v)P_3(u,\,v)P3(u,v) :( u, v∈[0, 1]u,\,v\in[0,\,1]u,v∈[0,1] )
P3(u, v)=[F0(u)F1(u)G0(u)G1(u)][P(0,0)P(0,1)Pv(0,0)Pv(0,1)P(1,0)P(1,1)Pv(1,0)Pv(1,1)Pu(0,0)Pu(0,1)Puv(0,0)Puv(0,1)Pu(1,0)Pu(1,1)Puv(1,0)Puv(1,1)][F0(v)F1(v)G0(v)G1(v)]
P_3(u,\,v)=
\begin{bmatrix}
F_0(u) & F_1(u) & G_0(u) & G_1(u)
\end{bmatrix}
\begin{bmatrix}
P(0,0) & P(0,1) & P_v(0,0) & P_v(0,1) \\
P(1,0) & P(1,1) & P_v(1,0) & P_v(1,1) \\
P_u(0,0) & P_u(0,1) & P_{uv}(0,0) & P_{uv}(0,1) \\
P_u(1,0) & P_u(1,1) & P_{uv}(1,0) & P_{uv}(1,1) \\
\end{bmatrix}
\begin{bmatrix}
F_0(v) \\ F_1(v) \\ G_0(v) \\ G_1(v)
\end{bmatrix}
\quad\quad
P3(u,v)=[F0(u)F1(u)G0(u)G1(u)]⎣⎡P(0,0)P(1,0)Pu(0,0)Pu(1,0)P(0,1)P(1,1)Pu(0,1)Pu(1,1)Pv(0,0)Pv(1,0)Puv(0,0)Puv(1,0)Pv(0,1)Pv(1,1)Puv(0,1)Puv(1,1)⎦⎤⎣⎡F0(v)F1(v)G0(v)G1(v)⎦⎤
③ P(u, v)=P1(u, v)+P2(u, v)−P3(u, v)P(u,\,v)=P_1(u,\,v)+P_2(u,\,v)-P_3(u,\,v)P(u,v)=P1(u,v)+P2(u,v)−P3(u,v) 便是所要构造的面,矩阵形式为:( u, v∈[0, 1]u,\,v\in[0,\,1]u,v∈[0,1] )
P(u, v)=−[−1F0(u)F1(u)G0(u)G1(u)][0P(u,0)P(u,1)Pv(u,0)Pv(u,1)P(0,v)P(0,0)P(0,1)Pv(0,0)Pv(0,1)P(1,v)P(1,0)P(1,1)Pv(1,0)Pv(1,1)Pu(0,v)Pu(0,0)Pu(0,1)Puv(0,0)Puv(0,1)Pu(1,v)Pu(1,0)Pu(1,1)Puv(1,0)Puv(1,1)][−1F0(v)F1(v)G0(v)G1(v)]
P(u,\,v)= -
\begin{bmatrix}
-1 & F_0(u) & F_1(u) & G_0(u) & G_1(u)
\end{bmatrix}
\begin{bmatrix}
0 & P(u,0) & P(u,1) & P_v(u,0) & P_v(u,1) \\
P(0,v) & P(0,0) & P(0,1) & P_v(0,0) & P_v(0,1) \\
P(1,v) & P(1,0) & P(1,1) & P_v(1,0) & P_v(1,1) \\
P_u(0,v) & P_u(0,0) & P_u(0,1) & P_{uv}(0,0) & P_{uv}(0,1) \\
P_u(1,v) & P_u(1,0) & P_u(1,1) & P_{uv}(1,0) & P_{uv}(1,1) \\
\end{bmatrix}
\begin{bmatrix}
-1 \\ F_0(v) \\ F_1(v) \\ G_0(v) \\ G_1(v)
\end{bmatrix}
\quad\quad
P(u,v)=−[−1F0(u)F1(u)G0(u)G1(u)]⎣⎡0P(0,v)P(1,v)Pu(0,v)Pu(1,v)P(u,0)P(0,0)P(1,0)Pu(0,0)Pu(1,0)P(u,1)P(0,1)P(1,1)Pu(0,1)Pu(1,1)Pv(u,0)Pv(0,0)Pv(1,0)Puv(0,0)Puv(1,0)Pv(u,1)Pv(0,1)Pv(1,1)Puv(0,1)Puv(1,1)⎦⎤⎣⎡−1F0(v)F1(v)G0(v)G1(v)⎦⎤





 博客主要介绍了B样条曲线与曲面、NURBS曲线与曲面以及Coons曲面相关知识。阐述了B样条曲线方程定义、基函数性质、类型划分等,介绍了NURBS曲线定义、性质及权因子意义,还说明了Coons曲面的构造方法,包括双线性和双三次Coons曲面。
博客主要介绍了B样条曲线与曲面、NURBS曲线与曲面以及Coons曲面相关知识。阐述了B样条曲线方程定义、基函数性质、类型划分等,介绍了NURBS曲线定义、性质及权因子意义,还说明了Coons曲面的构造方法,包括双线性和双三次Coons曲面。

















 1051
1051

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










