import sys
import random
import heapq
from collections import deque
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文显示问题
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
class StochasticNetworkFlowOptimizer:
def __init__(self, n, edges, source, sink, visualize=True, stochastic_demands=None):
"""
:param n: 节点数
:param edges: 边列表 [(u, v, lb, ub, cost)]
:param source: 源点
:param sink: 汇点
:param visualize: 是否可视化
:param stochastic_demands: 随机需求字典 {节点: (均值, 标准差)}
"""
self.n = n
self.source = source
self.sink = sink
self.original_edges = edges.copy()
self.visualize = visualize
self.stochastic_demands = stochastic_demands or {}
if visualize:
self.fig, self.ax = plt.subplots(figsize=(14, 10))
self.fig.suptitle("网络流随机优化问题求解", fontsize=16)
# 初始化超级源汇
self.super_source = n
self.super_sink = n + 1
self.total_nodes = n + 2
# 计算每个节点的流量差,考虑随机需求
self.A = [0] * (n + 2)
for u, v, lb, ub, cost in self.original_edges:
self.A[u] -= lb
self.A[v] += lb
# 添加随机需求
for node, (mean, std) in self.stochastic_demands.items():
# 使用均值作为初始需求
self.A[node] += mean
# 添加源汇之间无限容量的边
edges.append((sink, source, 0, float('inf'), 0))
# 创建图数据结构
self.graph = [[] for _ in range(self.total_nodes)]
self.dist = [float('inf')] * self.total_nodes
self.vis = [False] * self.total_nodes
self.pre = [-1] * self.total_nodes
self.edge_info = {}
self.total_cost = 0
self.iteration_count = 0
self.max_flow_value = 0
# 添加图中的边
self.edge_refs = []
for i, (u, v, lb, ub, cost) in enumerate(edges):
cap = ub - lb
self.add_edge(u, v, cap, cost, (i, lb, ub, cost, f"e{i}"))
if i < len(edges) - 1:
self.edge_refs.append((u, v, len(self.graph[u]) - 1, lb))
# 添加超级源汇的边
self.total_flow = 0
for i in range(n + 2):
if self.A[i] > 0:
self.add_edge(self.super_source, i, self.A[i], 0, (f"S→{i}", "super_source"))
self.total_flow += self.A[i]
elif self.A[i] < 0:
self.add_edge(i, self.super_sink, -self.A[i], 0, (f"{i}→T", "super_sink"))
# 初始化可视化
if visualize:
self.initialize_visualization()
def add_edge(self, u, v, cap, cost, info=None):
"""添加边并存储信息"""
edge_data = {
'capacity': cap,
'cost': cost,
'flow': 0,
'info': info
}
forward = [v, cap, cost, None, edge_data]
reverse = [u, 0, -cost, None, None]
forward[3] = reverse
reverse[3] = forward
self.graph[u].append(forward)
self.graph[v].append(reverse)
if info:
self.edge_info[(u, v)] = edge_data
return forward
def spfa(self, s, t):
"""SPFA算法寻找最小费用增广路径"""
self.dist = [float('inf')] * self.total_nodes
self.vis = [False] * self.total_nodes
self.pre = [-1] * self.total_nodes
self.dist[s] = 0
self.vis[s] = True
queue = deque([s])
if self.visualize:
self.visualize_step(f"SPFA: 寻找最小费用路径 (迭代 {self.iteration_count})")
while queue:
u = queue.popleft()
self.vis[u] = False
for idx, edge in enumerate(self.graph[u]):
v, cap, cost, rev, edge_data = edge
if cap > 0 and self.dist[u] + cost < self.dist[v]:
self.dist[v] = self.dist[u] + cost
self.pre[v] = (u, idx)
if not self.vis[v]:
self.vis[v] = True
queue.append(v)
return self.dist[t] < float('inf')
def min_cost_flow(self):
"""计算最小费用流"""
total_flow = 0
self.iteration_count = 0
while self.spfa(self.super_source, self.super_sink):
flow = float('inf')
cur = self.super_sink
path_nodes = []
# 计算增广路径上的最小容量
while cur != self.super_source:
u, idx = self.pre[cur]
edge = self.graph[u][idx]
path_nodes.append(cur)
flow = min(flow, edge[1])
cur = u
path_nodes.append(self.super_source)
path_nodes.reverse()
# 更新增广路径上的流量
cur = self.super_sink
while cur != self.super_source:
u, idx = self.pre[cur]
edge = self.graph[u][idx]
rev_edge = edge[3]
edge[1] -= flow
rev_edge[1] += flow
if edge[4]:
edge[4]['flow'] += flow
self.total_cost += flow * edge[2]
# 更新可视化信息
if (u, cur) in self.edge_info:
self.edge_info[(u, cur)]['flow'] += flow
elif (cur, u) in self.edge_info:
self.edge_info[(cur, u)]['flow'] -= flow
cur = u
total_flow += flow
self.iteration_count += 1
if self.visualize:
self.visualize_step(f"更新流量: {flow} (总费用: {self.total_cost})")
# 检查可行解
if total_flow != self.total_flow:
if self.visualize:
self.visualize_step(f"无可行解! 需求流量: {self.total_flow}, 实际流量: {total_flow}")
return None, None
# 计算原图中每条边的实际流量
flows = []
for u, v, idx, lb in self.edge_refs:
if u == self.sink and v == self.source:
continue
edge = self.graph[u][idx]
actual_flow = lb + (self.edge_info[(u, v)]['capacity'] - edge[1])
flows.append(actual_flow)
self.max_flow_value = sum(flows)
if self.visualize:
self.visualize_final_flow(flows)
return flows, self.total_cost
def monte_carlo_simulation(self, num_samples=100):
"""蒙特卡洛模拟随机需求"""
if not self.stochastic_demands:
print("没有随机需求,无需模拟")
return self.min_cost_flow()
results = []
print(f"开始蒙特卡洛模拟 ({num_samples} 次迭代)")
for i in range(num_samples):
# 生成随机需求
for node, (mean, std) in self.stochastic_demands.items():
demand = max(0, int(np.random.normal(mean, std)))
# 更新节点流量差
self.A[node] += demand - self.stochastic_demands[node][0]
# 重新计算超级源汇的边
self.update_super_edges()
# 计算最小费用流
flows, cost = self.min_cost_flow()
if flows is not None:
results.append({
'flows': flows,
'cost': cost,
'demands': self.A.copy()
})
# 重置需求为均值
for node, (mean, std) in self.stochastic_demands.items():
self.A[node] += self.stochastic_demands[node][0] - demand
return results
def update_super_edges(self):
"""更新超级源汇的边以反映需求变化"""
# 移除旧的超级源汇边
self.graph[self.super_source] = []
self.graph[self.super_sink] = []
# 添加新的超级源汇边
self.total_flow = 0
for i in range(self.n + 2):
if self.A[i] > 0:
self.add_edge(self.super_source, i, self.A[i], 0, (f"S→{i}", "super_source"))
self.total_flow += self.A[i]
elif self.A[i] < 0:
self.add_edge(i, self.super_sink, -self.A[i], 0, (f"{i}→T", "super_sink"))
def optimize_robust_flow(self, robustness_level=0.1):
"""鲁棒优化:考虑需求波动"""
print(f"执行鲁棒优化 (鲁棒性级别: {robustness_level})")
# 调整需求以考虑最坏情况
for node, (mean, std) in self.stochastic_demands.items():
# 增加需求以考虑不确定性
adjusted_demand = mean + robustness_level * std
# 更新节点流量差
self.A[node] += adjusted_demand - mean
# 更新超级源汇的边
self.update_super_edges()
# 计算最小费用流
flows, cost = self.min_cost_flow()
return flows, cost
def get_node_label(self, node):
"""获取节点标签"""
if node == self.super_source:
return "S"
elif node == self.super_sink:
return "T"
elif node == self.source:
return f"源点({node})"
elif node == self.sink:
return f"汇点({node})"
else:
return f"{node}"
def initialize_visualization(self):
"""初始化可视化布局"""
self.G = nx.DiGraph()
# 添加节点
for i in range(self.n):
self.G.add_node(i, label=f"{i}")
self.G.add_node(self.super_source, label="S")
self.G.add_node(self.super_sink, label="T")
# 添加边
for u in range(self.total_nodes):
for edge in self.graph[u]:
v, cap, cost, rev, edge_data = edge
if cap > 0:
self.G.add_edge(u, v, capacity=cap, cost=cost, flow=0)
# 创建环形布局
self.pos = {}
angles = np.linspace(0, 2 * np.pi, self.n, endpoint=False)
for i in range(self.n):
angle = angles[i]
self.pos[i] = (np.cos(angle), np.sin(angle))
# 特殊节点位置
self.pos[self.source] = (0, 1.2)
self.pos[self.sink] = (0, -1.2)
self.pos[self.super_source] = (-1.5, 0)
self.pos[self.super_sink] = (1.5, 0)
# 初始绘图
self.ax.clear()
node_colors = []
for node in self.G.nodes():
if node == self.source or node == self.sink:
node_colors.append('lightgreen')
elif node == self.super_source or node == self.super_sink:
node_colors.append('salmon')
else:
node_colors.append('lightblue')
nx.draw_networkx_nodes(self.G, self.pos, node_size=800, node_color=node_colors)
nx.draw_networkx_labels(self.G, self.pos,
labels={n: d['label'] for n, d in self.G.nodes(data=True)})
# 绘制边
self.edge_collection = nx.draw_networkx_edges(
self.G, self.pos, arrowstyle='->', arrowsize=20,
edge_color='gray', width=1, ax=self.ax
)
# 初始化边标签
self.edge_labels = {}
for u, v in self.G.edges():
self.edge_labels[(u, v)] = self.ax.text(0, 0, "",
fontsize=8, ha='center', va='center')
self.ax.set_title("初始化网络", fontsize=14)
self.ax.set_axis_off()
plt.tight_layout()
plt.pause(2.0)
def visualize_step(self, message):
"""可视化当前步骤"""
self.ax.clear()
# 节点颜色
node_colors = []
for node in self.G.nodes():
if node == self.source or node == self.sink:
node_colors.append('lightgreen')
elif node == self.super_source or node == self.sink:
node_colors.append('salmon')
else:
node_colors.append('lightblue')
# 绘制节点
nx.draw_networkx_nodes(self.G, self.pos, node_size=800, node_color=node_colors)
nx.draw_networkx_labels(self.G, self.pos,
labels={n: d['label'] for n, d in self.G.nodes(data=True)})
# 绘制边并设置颜色和宽度
edge_colors = []
edge_widths = []
for u, v in self.G.edges():
cap = self.G[u][v]['capacity']
flow = self.edge_info.get((u, v), {}).get('flow', 0)
saturation = flow / cap if cap > 0 else 0
edge_colors.append(plt.cm.RdYlGn(saturation))
edge_widths.append(1 + 3 * saturation)
nx.draw_networkx_edges(
self.G, self.pos, arrowstyle='->', arrowsize=20,
edge_color=edge_colors, width=edge_widths, ax=self.ax
)
# 更新边标签
for (u, v), text in self.edge_labels.items():
cap = self.G[u][v]['capacity']
cost = self.G[u][v]['cost']
flow = self.edge_info.get((u, v), {}).get('flow', 0)
if u == self.super_source or v == self.super_sink:
label = f"{flow}/{cap}\n费用:0"
else:
info = self.edge_info.get((u, v), {}).get('info', None)
if info and isinstance(info, tuple):
_, lb, ub, cost_val, name = info
actual_flow = lb + flow
label = f"{name}: {actual_flow}/{ub}\n费用:{cost_val}\n[{lb},{ub}]"
else:
label = f"{flow}/{cap}\n费用:{cost}"
x = (self.pos[u][0] + self.pos[v][0]) / 2
y = (self.pos[u][1] + self.pos[v][1]) / 2
text.set_position((x, y))
text.set_text(label)
self.ax.add_artist(text)
# 显示当前信息
title = f"{message}\n总费用: {self.total_cost}"
if self.stochastic_demands:
title += f"\n随机需求节点: {len(self.stochastic_demands)}"
self.ax.set_title(title, fontsize=14)
self.ax.set_axis_off()
plt.tight_layout()
plt.draw()
plt.pause(0.5)
def visualize_final_flow(self, flows):
"""可视化最终流分配"""
self.ax.clear()
# 创建仅包含原图节点和边的子图
H = nx.DiGraph()
for i in range(self.n):
H.add_node(i, label=f"{i}")
# 添加原图边
for i, (u, v, lb, ub, cost) in enumerate(self.original_edges):
if i >= len(flows):
continue
H.add_edge(u, v, flow=flows[i], lb=lb, ub=ub, cost=cost, name=f"e{i}")
# 使用原布局
pos = {k: v for k, v in self.pos.items() if k in H.nodes()}
# 绘制节点
node_colors = []
for node in H.nodes():
if node in self.stochastic_demands:
# 随机需求节点用特殊颜色
node_colors.append('gold')
elif node == self.source or node == self.sink:
node_colors.append('lightgreen')
else:
node_colors.append('lightblue')
nx.draw_networkx_nodes(H, pos, node_size=800, node_color=node_colors)
nx.draw_networkx_labels(H, pos)
# 绘制边并设置颜色和宽度
edge_colors = []
edge_widths = []
for u, v in H.edges():
flow = H[u][v]['flow']
ub = H[u][v]['ub']
saturation = flow / ub
edge_colors.append(plt.cm.RdYlGn(saturation))
edge_widths.append(1 + 3 * saturation)
nx.draw_networkx_edges(
H, pos, arrowstyle='->', arrowsize=20,
edge_color=edge_colors, width=edge_widths, ax=self.ax
)
# 添加边标签
edge_labels = {}
for u, v in H.edges():
flow = H[u][v]['flow']
lb = H[u][v]['lb']
ub = H[u][v]['ub']
cost = H[u][v]['cost']
name = H[u][v]['name']
edge_labels[(u, v)] = f"{name}: {flow}\n费用:{cost}\n[{lb},{ub}]"
nx.draw_networkx_edge_labels(H, pos, edge_labels=edge_labels, font_size=8)
# 添加随机需求信息
demand_info = "\n随机需求节点:\n"
for node, (mean, std) in self.stochastic_demands.items():
demand_info += f"节点 {node}: 均值={mean}, 标准差={std}\n"
title = f"最优流分配 (总流量: {self.max_flow_value}, 总费用: {self.total_cost})\n{demand_info}"
self.ax.set_title(title, fontsize=14)
self.ax.set_axis_off()
plt.tight_layout()
plt.draw()
def stochastic_flow_optimization(n, edges, source, sink, stochastic_demands=None,
optimization_mode="min_cost", num_samples=100,
robustness_level=0.1):
"""
网络流随机优化求解
:param n: 节点数
:param edges: 边列表 [(u, v, lb, ub, cost)]
:param source: 源点
:param sink: 汇点
:param stochastic_demands: 随机需求字典 {节点: (均值, 标准差)}
:param optimization_mode: 优化模式 ("min_cost", "robust", "monte_carlo")
:param num_samples: 蒙特卡洛模拟样本数
:param robustness_level: 鲁棒优化级别
:return: 优化结果
"""
optimizer = StochasticNetworkFlowOptimizer(
n, edges, source, sink, visualize=True,
stochastic_demands=stochastic_demands
)
if optimization_mode == "min_cost":
print("执行最小费用流优化")
flows, cost = optimizer.min_cost_flow()
return {'flows': flows, 'cost': cost}
elif optimization_mode == "robust":
print("执行鲁棒优化")
flows, cost = optimizer.optimize_robust_flow(robustness_level)
return {'flows': flows, 'cost': cost}
elif optimization_mode == "monte_carlo":
print("执行蒙特卡洛模拟")
results = optimizer.monte_carlo_simulation(num_samples)
# 分析结果
if results:
avg_cost = sum(r['cost'] for r in results) / len(results)
min_cost = min(r['cost'] for r in results)
max_cost = max(r['cost'] for r in results)
print(f"蒙特卡洛结果: {len(results)}次模拟, 平均费用={avg_cost:.2f}, 最小={min_cost}, 最大={max_cost}")
# 返回所有结果和统计信息
return {
'results': results,
'avg_cost': avg_cost,
'min_cost': min_cost,
'max_cost': max_cost
}
return None
else:
raise ValueError(f"未知优化模式: {optimization_mode}")
if __name__ == "__main__":
# 复杂网络示例 (15节点)
print("=" * 50)
print("网络流随机优化问题求解")
n = 15
edges = [
# 源点→核心节点 (u, v, lb, ub, cost)
(0, 1, 5, 20, 2),
(0, 2, 5, 20, 3),
# 核心环状结构
(1, 2, 0, 10, 1),
(2, 3, 2, 15, 4),
(3, 4, 2, 15, 2),
(4, 1, 0, 10, 1),
# 核心→中间节点
(1, 5, 1, 10, 3),
(2, 6, 1, 10, 2),
(3, 7, 1, 10, 4),
(4, 8, 1, 10, 3),
# 中间层平衡结构
(5, 6, 0, 10, 1),
(6, 7, 0, 10, 2),
(7, 8, 0, 10, 1),
(8, 5, 0, 10, 3),
# 中间→汇点
(5, 14, 3, 15, 5),
(6, 14, 3, 15, 4),
(7, 14, 2, 15, 3),
(8, 14, 2, 15, 2),
# 连接外围节点
(1, 9, 0, 10, 2),
(2, 10, 0, 10, 3),
(3, 11, 0, 10, 1),
(4, 12, 0, 10, 2),
(9, 13, 0, 10, 4),
(10, 13, 0, 10, 2),
(11, 13, 0, 10, 3),
(12, 13, 0, 10, 1),
(13, 14, 0, 20, 2) # 汇点入口
]
# 设置源点和汇点
source = 0
sink = 14
# 设置随机需求 (节点: (均值, 标准差))
stochastic_demands = {
5: (8, 2), # 节点5有随机需求
7: (6, 1.5), # 节点7有随机需求
10: (4, 1), # 节点10有随机需求
12: (5, 1.2) # 节点12有随机需求
}
# 选择优化模式
optimization_mode = "robust" # 可选: "min_cost", "robust", "monte_carlo"
# 执行优化
result = stochastic_flow_optimization(
n, edges, source, sink,
stochastic_demands=stochastic_demands,
optimization_mode=optimization_mode,
num_samples=100,
robustness_level=0.2
)
if result:
if optimization_mode == "monte_carlo":
print(f"蒙特卡洛模拟结果: 平均费用={result['avg_cost']:.2f}")
else:
print(f"优化结果: 总费用={result['cost']}")
plt.show() # 保持窗口打开
C:\Users\25827\.conda\envs\torch\python.exe C:\Users\25827\Desktop\图论代码\网络流随机优化.py
==================================================
网络流随机优化问题求解
执行鲁棒优化
执行鲁棒优化 (鲁棒性级别: 0.2)
优化结果: 总费用=None
进程已结束,退出代码为 0
有问题吗,是不是太简单了
最新发布
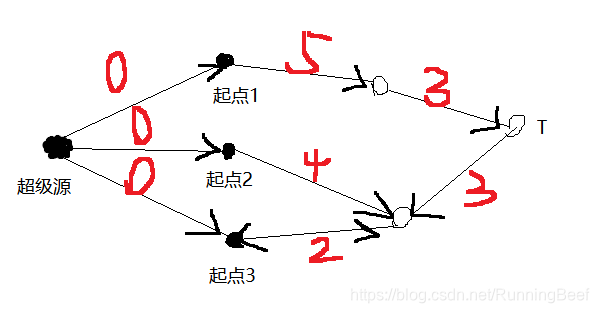





 本文介绍了解决多源最短路径问题的超级源点和解决多汇点最短路径问题的超级汇点概念。超级源点通过引入虚拟起点简化多起点最短路径计算,超级汇点通过引入虚拟终点简化多终点最短路径计算。
本文介绍了解决多源最短路径问题的超级源点和解决多汇点最短路径问题的超级汇点概念。超级源点通过引入虚拟起点简化多起点最短路径计算,超级汇点通过引入虚拟终点简化多终点最短路径计算。
















 2767
2767

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








