本文详细介绍了C++实现红黑树的插入、删除操作，包括插入节点的log级别调整和删除节点的log级别调整。同时，提供了检查红黑树正确性的方法，包括判断是否为BST、黑色平衡和根节点颜色。测试函数用于验证插入和删除操作的正确性，并提供了一个打印红黑树结构的函数，便于观察和调试。
RB_Tree
- c++ 实现的红黑树
- 包含插入、刪除、测试调整后的红黑树的正确性，打印红黑树
查找结点
- 根据结点key左小又大递归查询即可，用迭代也行。
插入结点 log级别
- 插入思路见维基百科红黑树 主要是对插入节点和插入节点的父节点兄弟节点等的颜色分类讨论。
- 注意当递归向上调整的时候，新的需要调整的点变成了一颗有儿子的树，所以调整插入节点的函数要把被调整的节点当作一颗树来调整，转移节点的时候，要注意调整原节点左右儿子的位置
- 注意考虑可能递归向上调整的情况，所以旋转时要把子树转移好
代码
/* 先找到合适位置插入，之后再根据父节点颜色判断是否进行调整 */
void insert(int key, T value)
{
Node *insertNode = new Node(key, value);
Node *traver = root;
while (traver)
{
if (key < traver->key)
{
if (traver->left_Son)
traver = traver->left_Son;
else
{
traver->left_Son = insertNode;
break;
}
}
else if (key > traver->key)
{
if (traver->right_Son)
traver = traver->right_Son;
else
{
traver->right_Son = insertNode;
break;
}
}
else /* 这个结点已经有过就更新 */
{
traver->value = value;
delete insertNode;
return;
}
}
insertNode->parent = traver;
insert_case1(insertNode);
}
/* 没有根结点 */
void insert_case1(Node *son)
{
cout << "insert_case1" << endl;
if (son->parent == nullptr)
{
root = son;
root->color = Black;
}
else
insert_case2(son);
}
/* 父节点是黑色结点，插入结点默认是红色结点，所以直接插入即可 */
void insert_case2(Node *son)
{
cout << "insert_case2" << endl;
if (son->parent->color == Black) /* 父节点是黑色结点，那么直接插入一个红色结点 不影响黑色平衡 */
return;
else /* 父节点是红色结点需要调整 */
insert_case3(son);
}
/* 父节点是红色结点，那么必定有祖父结点且为黑色。
当叔叔存在且是红色结点时将祖父结点变为红色。黑色下降，让父亲结点和叔叔结点都变为黑色.
考虑祖父结点的父节点可能为空（说明祖父结点是根结点，则只能把祖父结点变成黑色，也只有这种情况让黑色高度+1），或者祖父结点的父节点也可能为红色，
所以需要把祖父结点当做新插入的结点，进行插入做递归检查
可以思考下：是否影响了原树其他结点的黑色平衡？
*/
void insert_case3(Node *son)
{
cout << "insert_case3 " << endl;
if (get_uncle(son) && get_uncle(son)->color == Red)
{
// cout << "insert_case3 if" << endl;
get_uncle(son)->color = son->parent->color = Black;
get_grandparent(son)->color = Red;
/* 递归检查祖父结点 */
insert_case1(get_grandparent(son));
}
else
insert_case4(son);
}
/*
当叔叔结点为黑色或者为空时(我们把空的叶子节点也当做黑色结点)
需要做旋转，根据插入结点和插入结点的父节点结构做不同旋转
LL: 右旋一次 insert_case5
RR：左旋一次 insert_case5
LR：先左旋一次变为LL再来处理
RL：先右旋一次变为RR再处理
注意：这边新插入的结点是红色的，所以没有改变之前的黑色平衡
但是插入结点的父节点是红色的，所以需要调整
我们在调整的时候只要保证对应从祖父结点向下经过的黑色结点个数一样
就仍能保持黑色平衡
*/
void insert_case4(Node *son)
{
cout << "insert_case4" << endl;
/* 左右结构 调整为 左左结构 */
if (son == son->parent->right_Son && son->parent == get_grandparent(son)->left_Son)
{
// cout << "LR" << endl;
rotated_left(son);
son = son->left_Son;
} /* 右左结构 调整为 右右结构 */
else if (son == son->parent->left_Son && son->parent == get_grandparent(son)->right_Son)
{
// cout << "RL" << endl;
rotated_right(son);
son = son->right_Son;
}
/* 统一处理左左结构 和右右结构 */
insert_case5(son);
}
/* 当叔叔是黑色结点或空结点，且插入结点结构是LL 或者 RR */
void insert_case5(Node *son)
{
// cout << "insert_case5" << endl;
son->parent->color = Black;
get_grandparent(son)->color = Red;
/* 左左结构 右旋即可 */
if (son == son->parent->left_Son)
{
rotated_right(son->parent);
}
else
{ /* 右右结构 左旋即可 */
rotated_left(son->parent);
}
}
删除结点 log级别
- 采用了博客的删除做法，本来想继续使用维基百科的做法，但是不太合适。
- 现找到要删除结点的前驱结点，或者后继结点，然后和要删除的结点交换（只交换key和value，不交换结构），这样问题就变成了删除前驱结点或者后继结点。
调整时还是根据结点颜色分类讨论，情况复杂时对兄弟结点颜色进行讨论，会发现其妙的事情:) - 兄弟结点是黑色：兄弟结点的儿子全黑或全空直接处理，其他情况都可以转换成一种情况处理
- 兄弟结点是红色：旋转一次转换成兄弟结点是红色结点的情况
- 注意这里对删除后结点的调整还是要考虑想插入结点时调整的情况，考虑最后调整的结点是有左右儿子的，因为有些情况要递归向上调整
- 注意考虑可能递归向上调整的情况，所以旋转时要把子树转移好
代码
/*
交换要删除的结点和要删除的结点的前驱结点
删除原来结点的前驱结点注意删除后记得给指针置为nullptr
*/
bool erase(int key)
{
Node *traver = root;
while (traver)
{
cout << traver->key << endl;
if (key < traver->key)
traver = traver->left_Son;
else if (traver->key < key)
traver = traver->right_Son;
else
break;
}
/* 没有找到要删除的结点 */
if (traver == nullptr)
return false;
/* 获得前驱结点 */
Node *preNode = get_pre_node(traver->left_Son);
/* 将前驱结点和要删除结点的值交换，问题变为删除这个点的前驱结点
如果没有前驱结点删除自身*/
if (preNode)
swap(traver, preNode);
else
preNode = traver;
erase_adjust(preNode);
return true;
}
void erase_adjust(Node *son)
{
cout << "erase_adjust" << endl;
/* 特殊情况：删除结点是根 没有前驱结点 说明可能有右儿子且只能是红色结点 */
if (son == root)
{
root = son->right_Son;
if (root != nullptr)
root->color = Black;
delete son;
}
/* 特殊情况：这个结点是红色结点 不影响黑色平衡，且只有空儿子*/
else if (son->color == Red)
{
// cout << "???" << endl;
if (son->parent->left_Son == son)
son->parent->left_Son = nullptr;
else
son->parent->right_Son = nullptr;
delete son;
}
/* 特殊情况：被删除的结点为黑色且有左儿子 或者右儿子(因为这被删除的结点可能没有前驱结点，但是有右儿子)(红色）
则可以用红色结点代替黑色结点并重绘红色结点为黑色*/
else if (son->color == Black && son->left_Son != nullptr)
{
swap(son, son->left_Son);
delete son->left_Son;
son->left_Son = nullptr;
}
else if (son->color == Black && son->right_Son != nullptr)
{
swap(son, son->right_Son);
delete son->right_Son;
son->right_Son = nullptr;
}
else /* 要删除的结点是黑色结点且没有儿子
先调整这棵删除一个黑色结点后导致树的黑色平衡被打破的树
之后在真正删除那个需要删除的结点 根据具体情况分类讨论*/
{
/* 把这棵缺少一个黑色高度的树拿来调整（就是试着把兄弟树的结点匀过来一个保存黑色平衡，
如果不行那只能把父节点这颗大树整体黑色高度减1，
然后递归把父节点这颗大的树当做缺少一个黑色高度的树拿来调整） */
erase_case1(son);
if (son->parent && son->parent->left_Son == son)
son->parent->left_Son = nullptr;
else
son->parent->right_Son = nullptr;
delete son;
}
}
/* 按兄弟结点颜色分类讨论（被删除的点一定有兄弟结点） */
void erase_case1(Node *son)
{
cout << "erase_case1" << endl;
/* 当前需要调整的树是根 其实这个时候就不用调整了
其实是为erase_case6特别判断的一种情况*/
if (son == root)
return;
if (get_brother(son)->color == Black)
erase_case2(son);
else
erase_case3(son);
}
/* brother->color = Black */
void erase_case2(Node *son)
{
cout << " erase_case2 " << endl;
Node *brother = get_brother(son);
Node *parent = son->parent;
/* 兄弟结点有一个儿子为红 */
if ((brother->left_Son != nullptr && brother->left_Son->color == Red) || (brother->right_Son != nullptr && brother->right_Son->color == Red))
{
if (brother == parent->right_Son)
{
/* 调整成brother->right_Son->color = Red 的情况 然后左旋 再根据parent颜色 是否修改brother->right_Son颜色*/
/* 情况三：brother为黑色，且其左孩子是红色结点，右孩子是黑色结点或为空。 变为情况4*/
if (brother->right_Son == nullptr || brother->right_Son->color == Black)
{
rotated_right(brother->left_Son);
brother = brother->parent; /* 更新brother */
brother->color = Black;
brother->right_Son->color = Red;
}
// if (parent->color == Black)
// brother->right_Son->color = Black;
brother->color = parent->color;
parent->color = brother->right_Son->color = Black;
rotated_left(brother);
}
else /* 对称 */
{
/* 调整成brother->left_Son->color = Red */
if (brother->left_Son == nullptr || brother->left_Son->color == Black)
{
rotated_left(brother->right_Son);
brother = brother->parent;
brother->color = Black;
brother->left_Son->color = Red;
}
// if (parent->color == Black)
// brother->left_Son->color = Black;
brother->color = parent->color;
parent->color = brother->left_Son->color = Black;
rotated_right(brother);
}
}
else /* 兄弟结点左右儿子都为空 或者都是黑色*/
{
/* p黑 b黑 只能让parent黑色高度 - 1 ,然后继续调整parent*/
if (parent->color == Black)
{
brother->color = Red;
erase_case1(parent);
}
else
{
parent->color = Black;
brother->color = Red;
}
}
}
/* brother->color = Red
--> parent->color == brother->left_Son->color = brother->right_Son->color = Black*/
/* 转换成兄弟结点是黑色的情况 */
void erase_case3(Node *son)
{
cout << "erase case3" << endl;
Node *brother = get_brother(son);
Node *parent = brother->parent;
if (brother == parent->right_Son)
rotated_left(brother);
else
rotated_right(brother);
brother->color = Black;
parent->color = Red;
erase_case2(son);
}
测试红黑树代码是否正确
如何判断一棵红黑树是正确的？
- 判断是否是BST
- 任一结点到叶子节点路径上的黑色结点个数相同（黑色平衡）
- 没有连续量两个节点都是红色结点
- 根结点是否为黑色
- 结点的parent指针是否正确（调整的时候很容易忘记修改parent指针）
代码
/* 检查黑色平衡、指针、结点颜色，函数返回黑色高度 */
int check_tree(Node *temp)
{
if (temp == nullptr)
return 0;
/* 黑色节点计数，判断黑色平衡 */
int ct_black = 0;
if (temp->color == Black)
ct_black = 1;
/* 判断parent指针是否正确 */
if (temp->left_Son && temp->left_Son->parent != temp)
{
cout << temp->key << "ERROR: pointer left error: " << temp->left_Son->key << endl;
exit(-1);
}
if (temp->right_Son && temp->right_Son->parent != temp)
{
cout << temp->key << "ERROR: pointer right error: " << temp->right_Son->key << endl;
exit(-1);
}
/* 判断是否有两个连续红色节点 */
if (temp->color == Red)
{
// tourist();
if (temp->left_Son != nullptr && temp->left_Son->color == Red)
{
cout << temp->key << "ERROR: color error with left: " << temp->left_Son->key << endl;
exit(-1);
}
if (temp->right_Son != nullptr && temp->right_Son->color == Red)
{
cout << temp->key << "ERROR: color error with right: " << temp->right_Son->key << endl;
exit(-1);
}
}
/* 判断黑色平衡 */
int left_black = check_tree(temp->left_Son);
if (left_black != check_tree(temp->right_Son))
{
cout << temp->key << endl;
cout << "ERROR: check_Node error in color" << endl;
exit(-1);
}
return ct_black + left_black;
}
/* BST中序遍历的得到的key从小到大 */
void isValidBST(Node* root) {
stack<Node * > st;
Node * last = nullptr, * now = root;
while(true)
{
while(now != nullptr)
{
st.push(now);
now = now->left_Son;
}
if(st.size())
now = st.top();
else return ;
st.pop();
if(last != nullptr && now->key <= last->key)
{
std::cout << "EROOR: not BST" << std::endl;
exit(-1);
}
last = now;
now = now->right_Son;
}
return ;
}
/* 判断红黑树的正确性 */
void isVaildRbTree()
{
/* 判断是否是BST */
check_tree(root);
/* 判断红黑树其他要求 */
isValidBST(root);
if(root != nullptr && root->color == Red)
{
std::cout << "ERROR: root color is not black" << std::endl;
exit(-1);
}
}
如何编写测试函数
- 利用上面这3点编写一个测试红黑树正确性的check函数（递归返回黑色子树黑色高度，异常时exit(-1)并输出提示）
- 你可以随机生成若干个的结点的key,边插入到红黑树中，边把key保存到数组中，边调用check函数判断红黑树结构是否正确。如果过程中没有错误，说明插入代码是正确的（先不用重置随机数种子，这样你如果测试出问题，继续生成同样个数的结点，生成的随机数还是一样的，保证了数据的可复现性。
- 随机取出数组中的某个key，然后在红黑树中删除对应结点，边删除边调用check函数直到红黑树为空。如果过程中没有错误，说明删除代码是正确的。
代码
/* 测试函数 */
void test(int n)
{
RB_Tree<int> rbTree{};
map<int, int> mp; /* 标记已经生成的key */
vector<int> index; /* 保存key方便删除 */
/* 测试插入 */
while (n--)
{
/* 随机生成key */
int key;
while (mp.find(key = rand() % 1000) != mp.end())
{
}
mp[key] = 1;
/* 保存key */
index.push_back(key);
cout << "insert key: " << key << endl;
rbTree.insert(key, 1);
rbTree.check_tree(rbTree.get_root());
// rbTree.tourist();
}
cout << "--------------------------------" << endl;
cout << "--------------------------------" << endl;
/* 随机将插入的key删除 */
while (index.size())
{
/* 随机生成已有的key并删除对应结点 */
int id = rand() % index.size();
int key = index[id];
cout << "erase key: " << key << endl;
index.erase(index.begin() + id);
rbTree.erase(key);
rbTree.check_tree(rbTree.get_root());
// rbTree.tourist();
}
cout << "rb_tree test success" << endl;
}
打印红黑树
- 如过上面的测试通过了，那么我们肯定希望只看到结果，还希望看到整个过程中红黑树的样子吧！
- 如果上面的测试失败了（毕竟代码量不小，还涉及到指针，所以难免会有bug），那么这个时候我们不仅需要GDB做断点调试，还需打印出红黑树的结构，因为树的结点一多，很难模拟出树的样子的来判断具体错误位置和原因
如何漂亮的打印出红黑树呢？ - 把高度为h的二维红黑树（看成满二叉树）压缩看成只有一层
- 根结点在2^(h-1）的位置
- 根结点左儿子在2^(h-1) - 2(h - 2)的位置，右儿子在2^(h - 1) +2 ^(h - 2)的位置
- 以此类推每个结点应该所在的位置 n为对应高度满二叉树的结点数
- 左儿子坐标 = 父结点坐标 - n/结点当前高度
- 右儿子坐标 = 父节点坐标 + n/结点当前高度
- 使用层序遍历打印结点，如果前面的结点空了，打印空格计数替代
- 注意这种情况适合树节点个数不是很大的情况，否则因为有些位置前面没有结点，但是打印出每个结点的占位符不一定相等，不好把握个数，导致位置有点偏差,，而且电脑显示屏长度有限，结点个数一多一行就放不下了。
代码
/* 打印这颗红黑树 */
void tourist()
{
if (root == nullptr)
return;
/*
first:前置空格数 second:结点
左儿子坐标 = 父结点坐标 - n/结点当前高度
右儿子坐标 = 父节点坐标 + n/结点当前高度
*/
vector<pair<int, Node *>> a, b;
int n = 1 << get_height(root); /* 对应高度满二叉树结点个数 */
a.push_back(pair<int, Node *>(n >> 1, root));
int h = 2;
while (1)
{
int cnt = 0;
for (auto it : a)
{
/* 前面有空缺用空格替代 */
while (cnt < it.first)
{
++cnt;
printf(" ");
}
/*层序输出结点的键值 和 颜色 */
if (it.second->color)
printf("%3dB", it.second->key);
else
printf("%3dR", it.second->key);
if (it.second->left_Son)
{
b.push_back(pair<int, Node *>(it.first - (n >> h), it.second->left_Son));
}
if (it.second->right_Son)
{
b.push_back(pair<int, Node *>(it.first + (n >> h), it.second->right_Son));
}
}
cout << "\n\n\n";
++h;
a = b;
b.clear();
if (!a.size())
break;
}
}
效果图如下
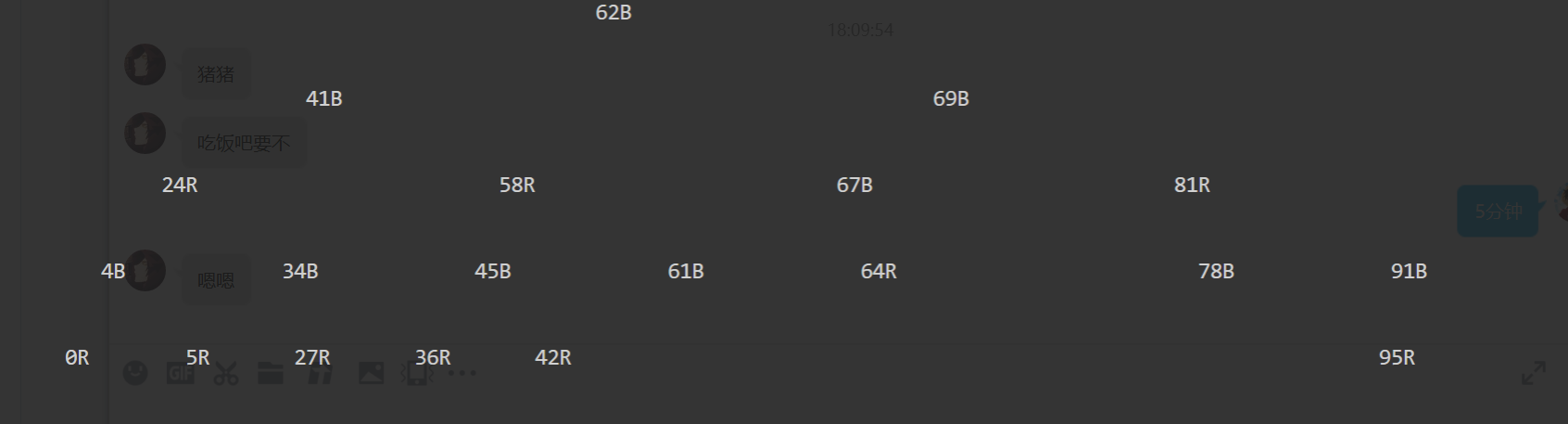
完整代码
/* 打印这颗红黑树 */
void tourist()
{
if (root == nullptr)
return;
/*
first:前置空格数 second:结点
左儿子坐标 = 父结点坐标 - n/结点当前高度
右儿子坐标 = 父节点坐标 + n/结点当前高度
*/
vector<pair<int, Node *>> a, b;
int n = 1 << get_height(root); /* 对应高度满二叉树结点个数 */
a.push_back(pair<int, Node *>(n >> 1, root));
int h = 2;
while (1)
{
int cnt = 0;
for (auto it : a)
{
/* 前面有空缺用空格替代 */
while (cnt < it.first)
{
++cnt;
printf(" ");
}
/*层序输出结点的键值 和 颜色 */
if (it.second->color)
printf("%3dB", it.second->key);
else
printf("%3dR", it.second->key);
if (it.second->left_Son)
{
b.push_back(pair<int, Node *>(it.first - (n >> h), it.second->left_Son));
}
if (it.second->right_Son)
{
b.push_back(pair<int, Node *>(it.first + (n >> h), it.second->right_Son));
}
}
cout << "\n\n\n";
++h;
a = b;
b.clear();
if (!a.size())
break;
}
}
扫一扫
1623
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
