矩阵的秩：小白也能懂的直观解释

快速体验

1. 打开 InsCode(快马)平台 https://www.inscode.net
2. 输入框内输入如下内容：

   开发一个交互式学习页面，直观展示矩阵的秩概念。包含：1. 可拖拽调整的2D/3D向量可视化工具；2. 实时计算并显示矩阵秩的变化；3. 用'橡皮筋'比喻解释线性相关/独立；4. 逐步引导的秩计算动画演示；5. 简单测验题和即时反馈。使用Plotly或类似库实现交互式可视化，适合零基础学习者。

3. 点击'项目生成'按钮，等待项目生成完整后预览效果

今天想和大家聊聊线性代数里一个听起来很吓人，但实际上非常有趣的概念——矩阵的秩。作为一个曾经被这个概念折磨过的过来人，我完全理解新手们的困惑。不过别担心，这次我们完全用最直观的方式来理解它。

秩到底是什么？

想象你手里有几根橡皮筋。如果这些橡皮筋互相独立，它们可以撑开一个空间；但如果有些橡皮筋是互相重叠的，那它们能撑开的空间就变小了。秩，就是这个空间中真正"有用"的橡皮筋的数量。

1. 在二维空间里，秩告诉我们有多少个不重合的方向
2. 在三维空间里，秩表示我们能找到多少个不平行的平面
3. 秩越大，说明矩阵包含的信息量越大

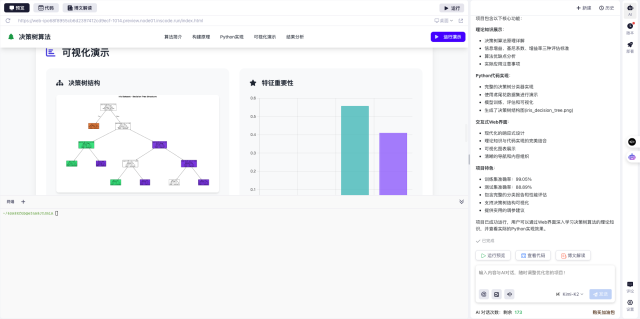
可视化理解

为了更直观地理解，我设计了一个交互式的学习工具（后面会教大家如何体验）。这个工具可以让你：

1. 用鼠标拖拽调整向量，实时看到秩的变化
2. 观察当向量变得线性相关时，秩如何减小
3. 通过动画演示秩的计算过程

比如当你把两个二维向量调整到同一条直线上时，秩会从2变成1，因为现在只有一个"有用"的方向了。

秩的实际意义

秩不仅仅是个数学概念，它在很多实际应用中都很重要：

1. 在机器学习中，秩可以帮助我们判断数据的冗余程度
2. 在图像处理中，秩与图像的压缩率密切相关
3. 在工程计算中，秩可以判断方程组是否有解

实战小测验

为了检验理解，可以试试回答这些问题：

1. 如果一个3x3矩阵的秩是2，意味着什么？
2. 如何判断两个向量是否线性相关？
3. 为什么单位矩阵的秩总是等于它的阶数？

（别担心答不出来，工具里有实时反馈功能可以帮你验证答案）

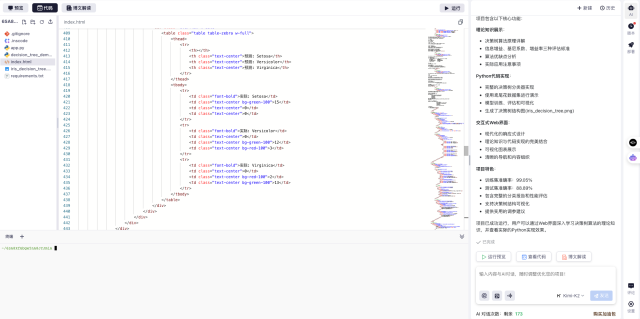
制作这个工具的技术细节

这个交互式学习页面是用Python的Plotly库实现的，主要特点是：

1. 响应式设计，支持桌面和移动设备
2. 实时计算核心，确保演示的准确性
3. 渐进式教学引导，从简单到复杂

体验建议

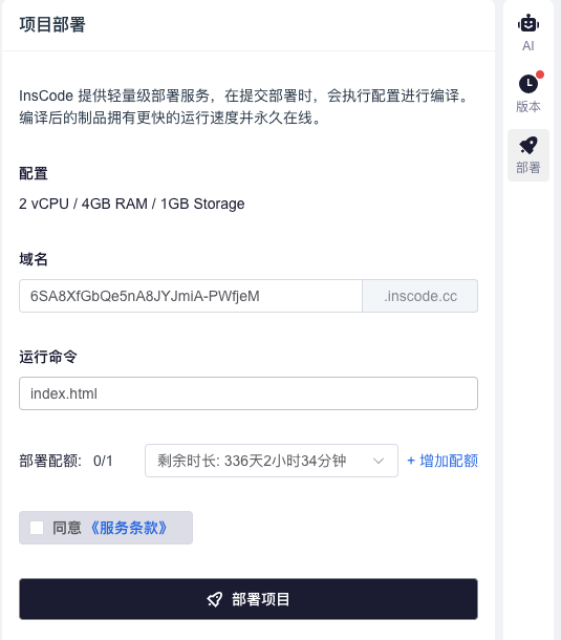
如果你也想亲自体验这个交互式学习工具，可以访问InsCode(快马)平台直接运行。我发现这个平台特别适合数学可视化项目的快速实现和分享，不需要配置复杂的环境，打开网页就能用。

最棒的是，平台支持一键部署功能，能把你的项目变成一个随时可以访问的在线应用。我测试时发现，从写完代码到上线运行，整个过程不到1分钟，对新手特别友好。

希望这个直观的解释和交互工具能帮你真正理解矩阵的秩。记住，数学概念最好的学习方式就是动手实践和可视化观察。

快速体验

1. 打开 InsCode(快马)平台 https://www.inscode.net
2. 输入框内输入如下内容：

   开发一个交互式学习页面，直观展示矩阵的秩概念。包含：1. 可拖拽调整的2D/3D向量可视化工具；2. 实时计算并显示矩阵秩的变化；3. 用'橡皮筋'比喻解释线性相关/独立；4. 逐步引导的秩计算动画演示；5. 简单测验题和即时反馈。使用Plotly或类似库实现交互式可视化，适合零基础学习者。

3. 点击'项目生成'按钮，等待项目生成完整后预览效果