第一次确定了(初始化):V0
所以放进S 这个确定集合里面,dis 是表示v0 到所有点的距离
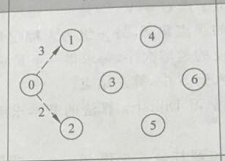
S【7】:.0
遍历:v0 – v1, v0 – v2
dis【7】: 0 3 2 inf inf inf inf
然后知道 到 v2 距离最短:2
所以
第二次确定了(作为新起始点):V2
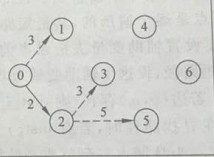
S【7】:0,2
遍历:v2 – v3,v2 – v5 //(接下不写了一个道理的,为了其他内容看些)
dis【7】: 0 3 2 5 inf 7 inf
因为从dis集合可以知道目前最短距离是:3 (为什么不是0或者2 呢,因为他们是已知的点了:v0 和v2,排除在外)
第三次确定(作为新起始点):V1
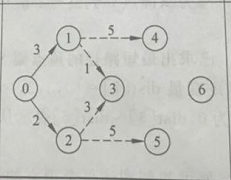
S【7】:0,2,1
dis【7】:0 3 2 4 8 7 inf
第四次确定(作为新起始点):V3
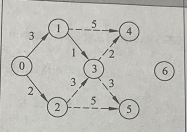
S【7】:0,2,1,3
dis【7】:0 3 2 4 6 7 inf
第五次确定(作为新起始点):V4
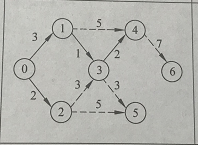
S【7】:0,2,1,3,4
dis【7】:0 3 2 4 6 7 13
第六次确认(作为新起始点):V5
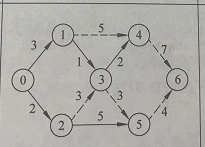
S【7】:0,2,1,3,4,5
dis【7】:0 3 2 4 6 7 11
第七次确认(作为新起始点):v6
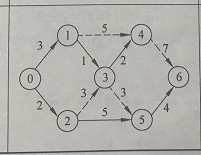

因为 S 集合此时 == 所有顶点,所以循环结束
总结:
-
每选一个起始点就意味着他的入度(即箭头指向的点)已经是最优化了,这也是贪心算法为什么每次选择最短距离边 (新起始点的入度边)的原因
-
每次选完一个起始点,遍历与之相连的下一个顶点且分别相加这些边,如果已经知道距离,例:v0到v4 距离18,经过遍历相加后发现新的路径同样可以到达距离只要:14
,则优化v0到v4距离为14
反正只要记住:每次选择的起始点已经被前个起始点优化到最优了。
c 和 MATLAB 代码待更





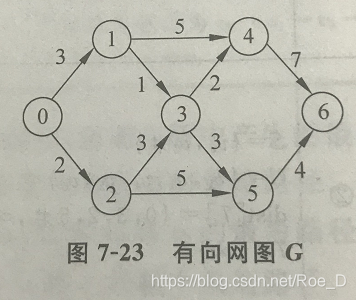
 本文深入讲解了Dijkstra算法的工作原理,通过实例展示了如何逐步优化路径,找到图中两点间的最短距离。每选一个起点意味着其入度已最优化,体现了贪心策略选择最短边的原则。
本文深入讲解了Dijkstra算法的工作原理,通过实例展示了如何逐步优化路径,找到图中两点间的最短距离。每选一个起点意味着其入度已最优化,体现了贪心策略选择最短边的原则。

















 1364
1364

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








