“距离”、“范数”和范数正则化

1. 范数

先思考 机器学习中的行向量和列向量？

1.1 概念

向量的范数可以简单形象的理解为向量到零点的距离，或者相应的两个点之间的距离、或者向量的长度。

(如果对象是一个单独的向量，那么默认是指与原点进行比较，这情况下，范数代表的是向量到原点的距离，也就是向量的向量的长度；如果定义了两个向量，则范数可以表示这两个向量之间的距离）

1.2 定义

向量的范数定义：向量的范数是一个函数||x||，满足
非负性 ||x|| >= 0，
齐次性 ||cx|| = |c| ||x|| ，
三角不等式 ||x+y|| <= ||x|| + ||y||。

1.3 常见的向量范数

• L1范数: ||x||₁ 为x向量各个元素绝对值之和。

• L2范数: ||x||₂为x向量各个元素平方和的1/2次方，L2范数又称Euclidean范数或者Frobenius范数

• Lp范数: ||x||_p为x向量各个元素绝对值p次方和的1/p次幂

• L∞范数: ||x||_∞为x所有向量元素中的最大值（向量各个元素绝对值最大那个元素的绝对值），如下：

  

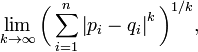
• 椭球向量范数: ||x||A = sqrt[T(x)Ax]， T(x)代表x的转置。定义矩阵C 为M个模式向量的协方差矩阵， 设C’是其逆矩阵，则Mahalanobis距离定义为||x||C’ = sq