数据结构与算法（1）入门篇

数据结构与算法整体框架

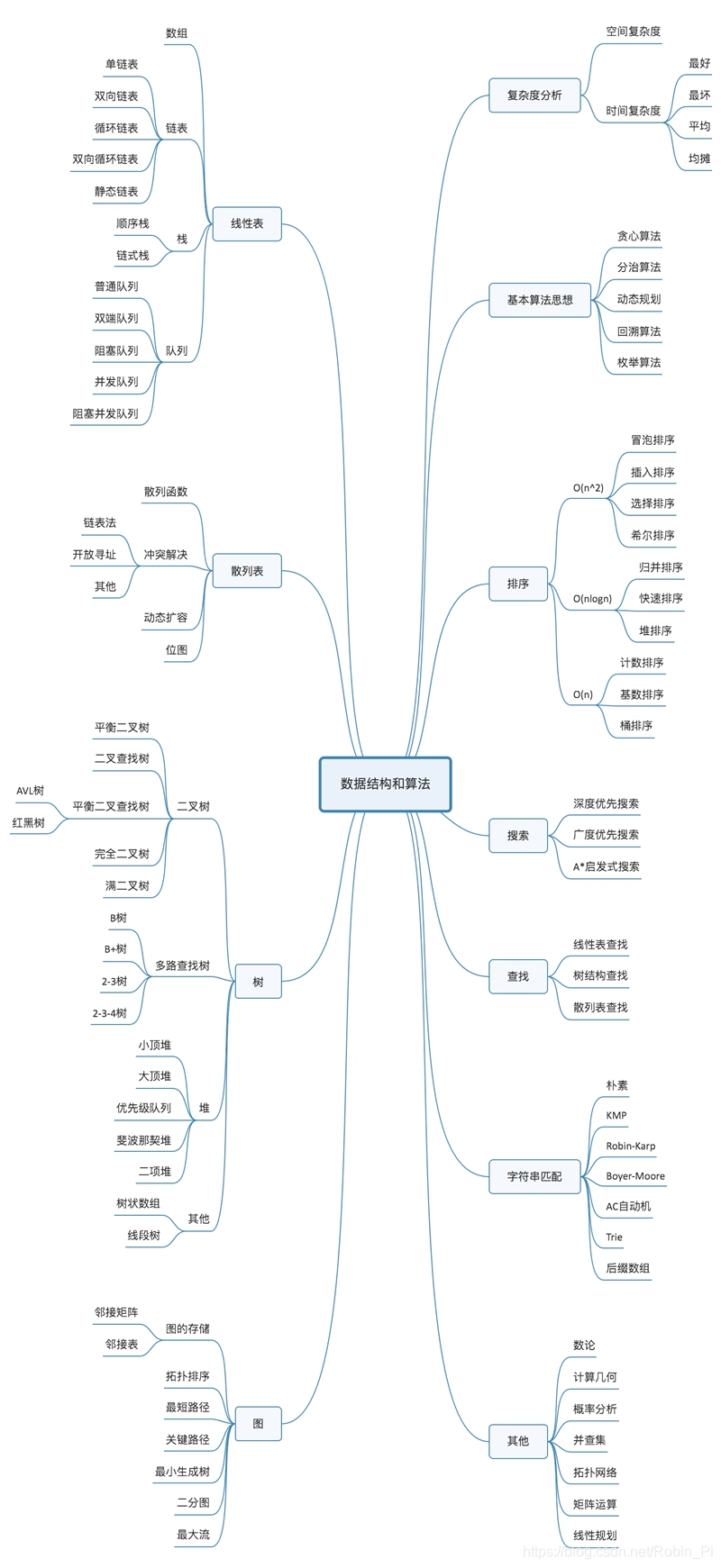
如何学

抓重点

• 20 个最常用的、最基础数据结构与算法：

10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树；

10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法。

掌握了这些基础的数据结构和算法，再学更加复杂的数据结构和算法，就会非常容易、非常快。

方法

在学习数据结构和算法的过程中，应当学习它的：

“来历”

“自身的特点”

“适合解决的问题”

以及“实际的应用场景”。

复杂度分析

复杂度分析是整个算法学习的精髓，只要掌握了它，数据结构和算法的内容基本上就掌握了一半。

大 O 复杂度表示法

从 CPU 的角度来看，这段代码的每一行都执行着类似的操作：读数据-运算-写数据。

尽管每行代码对应的 CPU 执行的个数、执行的时间都不一样，但是，我们这里只是粗略估计，所以可以假设每行代码执行的时间都一样，为 unit_time。

 int cal(int n) {
   int sum = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1;
     for (; j <= n; ++j) {
       sum = sum +  i * j;
     }
   }
 }

所有代码的执行时间 T(n) 与每行代码的执行次数 n 成正比。

把这个规律总结成一个公式:

T(n)=O(f(n))

T(n) 表示代码执行的时间；n 表示数据规模的大小；

f(n) 表示每行代码执行的次数总和。因为这是一个公式，所以用 f(n) 来表示。

公式中的 O，表示代码的执行时间 T(n) 与 f(n) 表达式成正比。

这就是大 O 时间复杂度表示法。大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

当 n 很大时，你可以把它想象成 10000、100000。而公式中的低阶、常量、系数三部分并不左右增长趋势，所以都可以忽略。

时间复杂度度 分析

三个比较实用的分析方法

1. 只关注循环执行次数最多的一段代码
2. 加法法则
   总复杂度等于量级最大的那段代码的复杂度
3. 乘法法则
   嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

多项式时间复杂度度分析

可以粗略地分为两类，多项式量级和非多项式量级。其中，非多项式量级只有两个：O(2^n) 和 O(n!)。

当数据规模 n 越来越大时，非多项式量级算法的执行时间会急剧增加，求解问题的执行时间会无限增长。所以，非多项式时间复杂度的算法其实是非常低效的算法。

我们主要来看几种常见的多项式时间复杂度。

1. O(1)

首先你必须明确一个概念，O(1) 只是常量级时间复杂度的一种表示方法，并不是指只执行了一行代码。比如这段代码，即便有 3 行，它的时间复杂度也是 O(1)，而不是 O(3)。

 int i = 8;
 int j = 6;
 int sum = i + j;

只要代码的执行时间不随 n 的增大而增长，这样代码的时间复杂度我们都记作 O(1)。或者说，一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。

2. O(logn)、O(nlogn)

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

 i=1;
 while (i <= n)  {
   i = i * 3;
 }

O(m+n)、O(m∗n)

这种时间复杂度，代码的复杂度由两个数据的规模来决定。

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

m 和 n 是表示两个数据规模，无法事先评估 m 和 n 谁的量级大，无法忽略其中一个，所以上面代码的时间复杂度就是 O(m+n)。

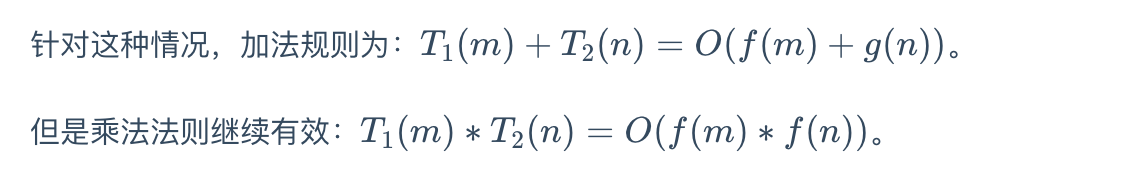
空间复杂度分析

空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的额外存储空间与数据规模之间的增长关系。

void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }

  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}

第 2 行代码中，申请了一个空间存储变量 i，但是它是常量阶的，跟数据规模 n 没有关系，所以可以忽略。

第 3 行申请了一个大小为 n 的 int 类型数组，除此之外，剩下的代码都没有占用更多的空间，所以整段代码的空间复杂度就是 O(n)。

我们常见的空间复杂度就是 O(1)、O(n)、O(n²)，像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。而且，空间复杂度分析比时间复杂度分析要简单很多。

渐进复杂度

渐进复杂度，包括时间复杂度和空间复杂度，用来分析算法执行效率与数据规模之间的增长关系，可以粗略地表示，越高阶复杂度的算法，执行效率越低。常见的复杂度并不多，从低阶到高阶有：

O(1)、O(logn)、O(n)、O(nlogn)、O(n²)。

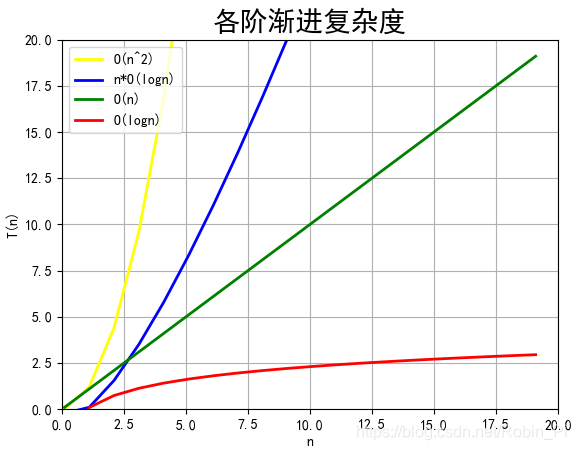渐进时间，渐进空间复杂度分析与是宿主平台无关的，能够让我们对我们的程序或算法有一个大致的认识，让我们知道，比如在最坏的情况下程序的执行效率如何。

算法1的时间复杂度是O(n)O(n)O(n)，算法2的时间复杂度是O(logn)O(logn)O(logn)，能立刻就对不同的算法有一个“效率”上的感性认识。

渐进式时间，空间复杂度分析只是一个理论模型，只能提供给粗略的估计分析，我们不能直接断定就觉得O(logN)的算法一定优于O(n), 针对不同的宿主环境，不同的数据集，不同的数据量的大小，在实际应用上面可能真正的性能会不同，针对不同的实际情况，进而进行一定的性能基准测试是很有必要的，比如在同一批手机上(同样的硬件，系统等等)进行横向基准测试，进而选择适合特定应用场景下的最有算法。

综上所述，渐进式时间，空间复杂度分析与性能基准测试并不冲突，而是相辅相成的，但是一个低阶的时间复杂度程序有极大的可能性会优于一个高阶的时间复杂度程序，所以在实际编程中，时刻关心理论时间，空间度模型是有助于产出效率高的程序的，同时，因为渐进式时间，空间复杂度分析只是提供一个粗略的分析模型，因此也不会浪费太多时间，重点在于在编程时，要具有这种复杂度分析的思维。

四种情况下时间复杂度分析

最好情况时间复杂度（best case time complexity）

最坏情况时间复杂度（worst case time complexity）

平均情况时间复杂度（average case time complexity）

均摊时间复杂度（amortized time complexity）

时间复杂度分析示例

分析一下下面这个 add() 函数的时间复杂度。

// 全局变量，大小为 10 的数组 array，长度 len，下标 i。
int array[] = new int[10]; 
int len = 10;
int i = 0;

// 往数组中添加一个元素
void add(int element) {
   if (i >= len) { // 数组空间不够了
     // 重新申请一个 2 倍大小的数组空间
     int new_array[] = new int[len*2];
     // 把原来 array 数组中的数据依次 copy 到 new_array
     for (int j = 0; j < len; ++j) {
       new_array[j] = array[j];
     }
     // new_array 复制给 array，array 现在大小就是 2 倍 len 了
     array = new_array;
     len = 2 * len;
   }
   // 将 element 放到下标为 i 的位置，下标 i 加一
   array[i] = element;
   ++i;
}