python小胶囊 - 集合与字典的存储方式-优快云博客

🧲TypeError问题引出

在定义字典和集合的时候, 可以发现一个有趣的现象:

>>> my_dict = {['name']:'John'}
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'

>>> nums1 = [1,2,3]
>>> nums2 = [4,5,6]
>>> new_nums = {nums1, nums2}
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'

可以看到, 如果将列表定义为字典的键, 或者尝试将列表合并为集合的时候, 就会弹出报错报错 TypeError: unhashable type: 'list' (列表是不可哈希类型)

🤨 这个哈希类型是从哪里来的?

这就需要去了解 “哈希是什么?” “哈希表是什么?”

🎞️ 哈希表的存储方式

哈希表(也称为散列表), 本质是通过哈希算法来实现的。

哈希算法是一种比较常见的加密算法, 将任意长度的输入数据映射为固定长度的输出数据, 这个输出值称为哈希值或者消息摘要。
哈希算法加密流程
在上面的定义中, 有两个重要的关键字"映射"和"固定长度"

“映射”: 通过散列函数来实现, 将输入的值变为地址的索引
“固定长度”: 在内存中, 分配的地址是有限的, 所以如果想要在有限的空间内进行存储, 就需要对应到固定的地址。

📍Note:

由于是经过同一个加密函数, 所以输入的相同数据也会得到相同的加密数据。

即具有相同内容的对象将具有相同的哈希值, 不同内容的对象具有不同的哈希值, 同时也可能拥有相同的哈希值(地址冲突)。

哈希表的特点:

查找速度快: 在合理的哈希函数下, 查找、插入和删除的时间复杂度接近O(1)
支持动态扩容: 当负载因子(Load Factor)超过阈值(如0.75)时, 哈希表会自动扩容以减少冲突

下面会提供案例以供更加深入理解其机制。

🩺 解决TypeError疑问

从上一章节"可变对象与不可变对象"中, 我们了解到列表、字典和集合都是是可变对象, 而可变对象在堆区中存储的内容是可修改的。

散列表是通过散列函数计算元素数据来得到元素存储位置的, 因此需要保证数据元素的哈希值在其生命周期内保持不变, 但可变对象的特性就决定了它无法成为可哈希对象。

🧪 创建哈希对象

内置函数hash()和hashlib()模块

内置函数hash()

作用: 用于计算不可变对象的哈希值

📍Note: python中的hash()调用的散列算法并不是固定的算法, 是经过改造的, 结果会根据对象类型和环境变量配置而有所不同

print(hash("hello"))  # 7013362525084595041
print(hash(3.14))  # 322818021289917443
print(hash((1, 2, 3))) # 529344067295497451

hashlib模块

hashlib模块实现了一个通用的接口来实现多个不同的安全哈希和摘要算法, 包括FIPS安全散列算法SHA1、SHA224、SHA256、SHA512以及RSA的MD5等。

常用方法:

hashlib.md5()/sha1()/sha256()...: 直接使用特定的算法创建哈希对象
hashlib.update(): 更新哈希对象的消息内容
hashlib.digest(): 获取二进制表示的哈希值
hashlib.hexdigest(): 获取十六进制表示的哈希值

import hashlib

def encrypt_pwd(password):
    # 如果已经确定了hash算法, 可以直接通过hashlib来模拟数据
    return hashlib.sha256(password.encode()).hexdigest()

stored_pwd = encrypt_pwd("aaa123!")
print(stored_pwd)

⌛ 集合的存储方式

在python中, 集合和字典都是以哈希表的方式来存储的, 下面用一个简单的案例来模拟一下。

定义一个长度为11的哈希表, 存储集合元素{77,56,92,13,49,29}
散列表模拟集合存储
映射方式: 将元素求余%哈希表长度(即11), 可以得到若干散列值 (如77%11=0)

元素	77	56	92	13	49	29
散列值	0	1	4	2	5	7

根据散列值将元素存储进散列表中
散列表插入集合元素

读取顺序与存入顺序的差异

在上面的散列表中, 存储元素的顺序与存入元素的顺序是不同的。因此在读取数据时, 如果按照上面的存储方式, 那么读取的数据为{77,56,13,92,49,29}

存储情况的评估: 负载因子

可以观察到, 在11个槽位中, 存储进6个元素, 可以计算出占用率为6/11, 这个占用率被称为"负载因子"。负载因子用来评判当前存储空间的使用情况, 如果值超出, 那么内存管理器就会分配更大的空间进行重新计算, 得到分配的新地址存储元素。

如果想要去搜索集合中存储的元素, 就可以不需要通过挨个遍历的方式去查找元素是否在集合中。

这种搜索的方式时间复杂度为O(1), 是非常高效的搜索算法。

🤔 如果这时想要存储一个新元素45( 45%11=1), 计算得到的槽位为1, 而槽位1已经有元素56, 应该如何解决?

🗃️ 哈希冲突的解决方法

上面的哈希冲突有两种解决方案:

方法1: 槽位1已经有元素56, 但是槽位3是空缺的, 可以填在槽位3

方法2: 槽位1已经有元素56, 但是可以通过链表的方式链接在元素56之后

其中方法1对应了"开放寻址法(open addressing)“, 方法2对应了"链表法(chaining)”

📬 开放寻址法

核心思想: 出现散列冲突, 重新探测新的空闲位置插入元素

包含有: 线性探测(Linear Probing), 平方探测(Quadratic probing)和双重散列(Double hashing)

下面根据"线性探测"给出案例:
冲突解决-线性探测法
但线性探测有个缺点, 就是哈希表中的元素会出现"聚集"现象, 如下图所示:
线性探测法缺点
为了解决这一问题, 就出现了"平方探测"和"双重散列"的方法, 本质上都是在出现冲突后按照新的避免聚集的方法找空缺重新填入新元素。

📪 链表法

核心思想: 出现散列冲突, 将冲突的元素以链表的方式存储在槽中。
冲突解决-链表法

📏 使用场景

开放寻址法: 小对象存储, 适合内存资源受限的环境

链表法: 大型对象存储, 高负载, 适合需要频繁操作对象的应用环境

📔 字典的存储方式

了解到上面集合的存储方式之后, 字典的存储方式就更容易理解一些了。

假设要存储一个字典: {'name':'Alice','age':30,'city':'London'}
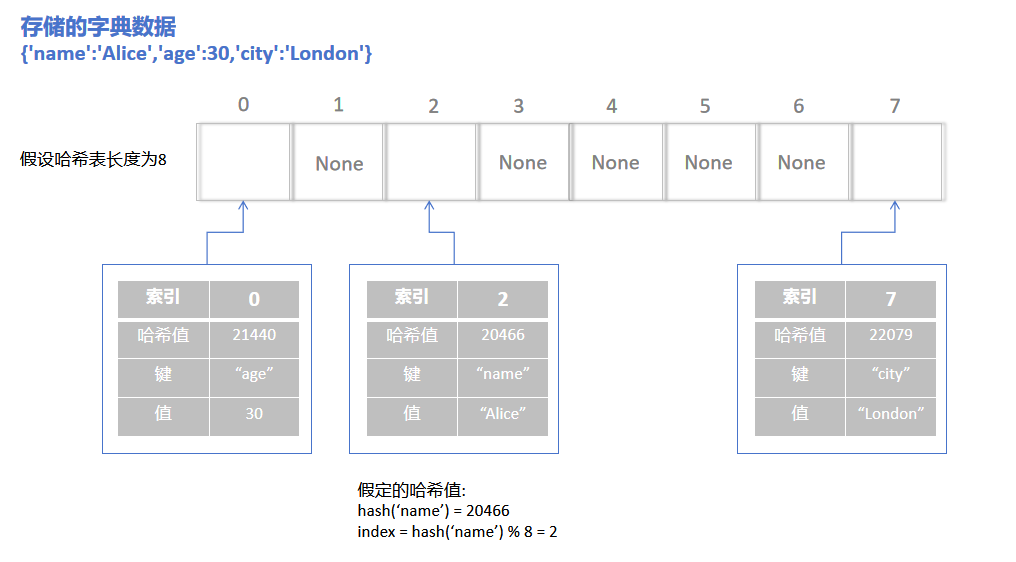
散列表-字典的存储
出现冲突后的解决方法也是"开放寻址法"和"链表法"。

🤔 如果是按照上面的存储方式来说的话, 在读取字典的时候, 读取出来的数据就应该是{'age':30, 'name':'Alice, 'city':'London'}, 但实际上通过python打印的时候仍然是原来的顺序 {''name':'Alice, age':30,'city':'London'}。为什么会这样?

🩺 疑问解答: 字典的"无序性"与"有序性"

查阅相关资料之后, 我发现python字典的存储架构是有过重大变动的。

上面的存储方式是python3.6以前的, 字典的存储顺序取决于哈希值和冲突处理策略, 因此键值对的顺序是不可预测的, 即遍历或打印时的顺序可能与插入的顺序完全不同。(字典的"无序性")

而从python3.6(Cpython)实现开始, 字典调整为新的存储架构, 将索引查找的逻辑与数据存储分离。字典的内部结构优化后保留了插入顺序, 并在python3.7被写入语言规范, 从此以后, 在遍历字典的时候, 键值对会按照插入的先后顺序返回。(字典的"有序性")

有序字典 `OrderedDict`

同时python还在collections模块中提供了一个字典子类OrderedDict, 通过其定义的字典, 也能够记住元素插入的顺序。

from collections import OrderedDict

dict1 = OrderedDict()
dict1['name'] = 'Alice'
dict1['age'] = 30
dict1['city'] = 'London'
print("有序字典: ", dict1)  # OrderedDict({'name': 'Alice', 'age': 30, 'city': 'London'})
print(type(dict1))  # <class 'collections.OrderedDict'>

dict2 = dict()
dict2['name'] = 'Alice'
dict2['age'] = 30
dict2['city'] = 'London'
print("普通字典: ", dict2) # {'name': 'Alice', 'age': 30, 'city': 'London'}
print(type(dict2))  # <class 'dict'>

可以看到, 有序字典和普通字典一样, 都是按照插入元素的顺序来返回的。

原本OrderedDict的出现是为了解决python3.6之前的字典无序性问题, 而python3.7之后仍然保留了下来, 它有一些特殊的功能还是很好用的。

功能1: 利用move_to_end()方法重新排序

from collections import OrderedDict

od = OrderedDict([('a', 1), ('b', 2), ('c', 3), ('d', 4)])

# 将元素a移动到末尾
od.move_to_end('a')
print(od)  # OrderedDict({'b': 2, 'c': 3, 'd': 4, 'a': 1})

# 将元素c移动到开头
od.move_to_end('c', last=False)
print(od)  # OrderedDict({'c': 3, 'b': 2, 'd': 4, 'a': 1})

功能2: 相等性比较

普通字典在对比两个字典是否相等时, 只比较内容, 不比较顺序。而有序字典对顺序是敏感的。

from collections import OrderedDict

d1 = {'a': 1, 'b': 2, 'c': 3}
d2 = {'b': 2, 'c': 3, 'a': 1}
print(d1 == d2)  # True

od1 = OrderedDict(d1)
od2 = OrderedDict(d2)
print(od1 == od2)  # False

功能3: 弹出操作控制

有序字典支持LIFO和FIFO两种弹出策略, 普通字典只支持LIFO策略

from collections import OrderedDict

od = OrderedDict({'a': 1, 'b': 2, 'c': 3})

# 弹出最后插入的元素(LIFO)
last_item = od.popitem(last=True)
print(last_item)  # ('c', 3)

# 弹出最先插入的元素(FIFO)
first_item = od.popitem(last=False)
print(first_item)  # ('a', 1)

# 普通字典只有一种弹出行为(LIFO)
d = {'a': 1, 'b': 2, 'c': 3}
item = d.popitem()
print(item)   # ('c', 3)

需要使用OrderedDict的情况

对存储的字典数据顺序比较敏感
LRU(Least Recently Used) 缓存实现 : 一种常见的缓存策略, 会在缓存满时删除最少使用的元素
需要FIFO队列行为

🎯总结

Python中的哈希存储方式

字典和集合都是由哈希表的方式来存储的, 哈希表由哈希算法实现。

哈希的本质是一种映射。将需要存储的元素映射成内存地址, 而映射的内存地址也可能存在冲突。

解决冲突的方法: 开放寻址法和链表法

模拟创建哈希对象

内置函数hash() 和 hashlib()模块

有序字典OrderedDict

python3.6之前字典是无序的, python3.7之后定义的字典是有序的。虽然已经有序, 但而有序字典OrderedDict仍有其易用性

功能1: 利用move_to_end()对字典进行重新排序
功能2: 字典的相等性比较(要求存储顺序一致)
功能3: 支持LIFO和FIFO两种弹出策略

文档参考:
浅谈算法-散列表(hash table)
利用线性探测法解决hash冲突
 python有序字典: 深入理解与高效使用
python数据结构与算法分析(第2版)